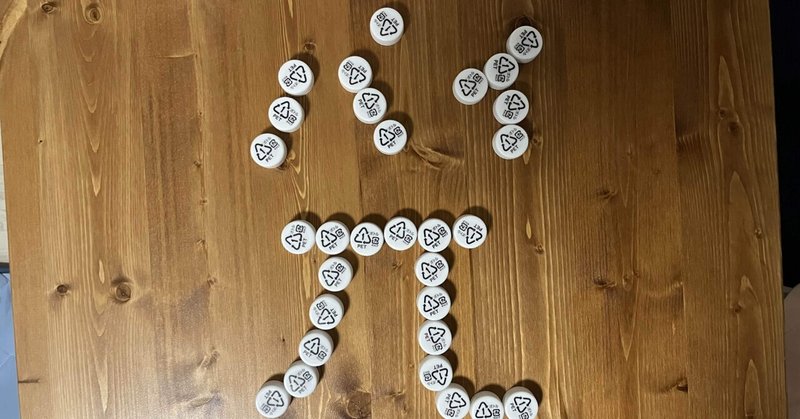- 運営しているクリエイター
記事一覧
【自由研究】ペットボトルキャップで数学してみた(ピタゴラス数)【後編】
前回の続きから書いていきます。
前回の記事はこちら↓↓
1 問題の確認問題
原始ピタゴラス数は{3,4,5}の他にもあるのか。あるなら具体例を示せ。
原始ピタゴラス数は無数にあるのか。あるなら生成する式を、ないならばそれを証明せよ。
2 前回の記事で見いだしたこと 最初に一辺の長さが$${n}$$の正方形があったとする。
この正方形の周りにペットボトルキャップを付け加えたとき、第$$
【自由研究】ペットボトルキャップで数学してみた(和)<後編>
こんにちは!!
閲覧いただき、ありがとうございます。
前回までの記事では、
$${1+2+3+・・・+n}$$
$${=\frac{1}{2}n(n+1)}$$
$${1^2+2^2+3^2+・・・+n^2}$$
$${=\frac{1}{6}n(n+1)(2n+1)}$$
になることを、ペットボトルキャップを使って示せました。
前回までの記事↓↓
今回は、
$${1^3+
【自由研究】ペットボトルキャップで数学してみた(和)<前編>
こんにちは!!
閲覧いただき、ありがとうございます。
以前も、家にある大量のペットボトルキャップで、こんなことしてみたんです↓↓
今回のテーマは、「和」です。
「和」とは足し算の結果のことで、今回はこんな和を考えます。
$${1+2+3+4+・・・+n}$$
$${1^2+2^2+3^2+4^2・・・+n^2}$$
$${1^3+2^3+3^3+4^3・・・+n^3}$$
「
【自由研究】ペットボトルキャップで数学してみた(和)<中編>
こんにちは!!
閲覧いただき、ありがとうございます。
前回の記事では、
$${1+2+3+・・・+n=\frac{1}{2}n(n+1)}$$という公式を、ペットボトルキャップを使って導きました。
前回の記事はこちら↓↓
今回は、前回の記事の「まとめ」で書いたことを生かして、
$${1^2+2^2+3^2+・・・+n^2}$$の公式を導いていきます。
これが今回の記事のゴールです。
【自由研究】正四面体は敷き詰められるだろうか??
こんにちは。
今回は、「敷き詰め」について、記事を書いてみました。
数式を使うところもありますが、数学が苦手な方も楽しんでもらえる記事にします。
いくつになっても自由研究してもいいですよね?笑
最後まで読んでいただけると、うれしいです!!
1 はじめに そもそも敷き詰めについて考えようと思ったきっかけは、先日紹介したこの公園のタイルを見てからです。
そこで、こんな疑問が浮かんだ