
【自由研究】ペットボトルキャップで数学してみた(和)<前編>
こんにちは!!
閲覧いただき、ありがとうございます。
以前も、家にある大量のペットボトルキャップで、こんなことしてみたんです↓↓
今回のテーマは、「和」です。
「和」とは足し算の結果のことで、今回はこんな和を考えます。
$${1+2+3+4+・・・+n}$$
$${1^2+2^2+3^2+4^2・・・+n^2}$$
$${1^3+2^3+3^3+4^3・・・+n^3}$$
「こんなの公式知ってるから、それに当てはめたらすぐできる!!」という方も多いと思いますが、その公式をペットボトルキャップを使って導出してみます。
実物を使ってやってみることで、私も新しい知見を得ることができました。
また、このテーマの記事を、前編・中編・後編に分けました。
あまりにも、長くなり過ぎましたので。
最後まで読んでいただけると、嬉しいです。
1 この自由研究をしようとしたきっかけ
そもそも、なぜこれをしようとしたのか。
それは、学生のころにこんな問題に出会ったからです。
$${n}$$を自然数とする。このとき、
$${1^3+2^3+3^3+4^3+・・・+n^3=(\frac{1}{2}n(n+1))^2}$$
であることを、数学的帰納法を使って証明しなさい。
この問題にある右辺の式$${(\frac{1}{2}n(n+1))^2}$$はどこから出てきたのだろうか?
この疑問は、私の中でずーっとくすぶり続けていました。。。
そこで、今回はこれを解決すべく、ペットボトルキャップで公式を導きだそう、という試みです。
流れは、目次の通りです。
2 ペットボトルキャップの”個数”が数を表す
例えば、自然数の「4」
これをペットボトルキャップで表すと、図1のようになります。

つまり配置は関係なく、ペットボトルキャップの数と自然数が対応しています。ただし、それぞれのペットボトルキャップは接していないといけないこととします。
3 足すとは??
数式で
$${1+2}$$
と表現された式。
これをペットボトルキャップで表現すると、
「付け加える」または「積み重ねる」と捉えることとします。



もちろん、「付け加える」と「積み重ねる」を両方使って「足す」と捉えてもよいこととします。
4 1+2+3+・・・n=??
いきなり$${1^3+2^3+3^3+4^3+・・・+n^3}$$の公式を導くのではなく、とっかかりやすいところから始めます。
ということでまずは、
$${1+2+3+4+・・・+n}$$
の公式を導きます。
方針としては、
$${1+2}$$、$${1+2+3}$$、$${1+2+3+4}$$を、それぞれペットボトルキャップで表現して、効率よく求める方法を見いだします。
それらからパターンを見つけ、
$${1+2+3+4+・・・+n}$$
に当てはめれば、公式化できます。
・ 1+2=

この計算をどうすれば効率よくできるのか?
横に付け加えたり、上に積み重ねたりすることはできますが、それでは1つずつ数えないといけないので、効率よくキャップの個数を求められません。
要は、数えるキャップの個数をなるべく減らすことが効率的な方法と言えそうです。
ではどうすればいいか。
それは、足し算をかけ算にすればいいのです。
例えば、
$${2+2+2+2=2×4}$$
とできます。

足し算だと〇を8回数えないといけませんが、かけ算だと6回で済みます。このように、数える回数を減らせます。
また、このときもう一つ大切なのは、かけ算に変えることは、〇(ペットボトルキャップ)で図形を作って面積や体積を求めることだということです。逆に、足し算は線の長さを求めているということです。

では、$${1+2}$$をかけ算にするにはどうするか。
付け加える位置が重要です。

図8は、三角形にも見えます。
三角形は、2つ組み合わせると平行四辺形にできます。
平行四辺形は、長方形に変形できます。(図9)

つまり、足し算をかけ算にする流れを式で表すと、こうなります。
$${(1+2)+(1+2)=2×3}$$
$${1+2=\frac{1}{2}×2×3}$$
・ 1+2+3=
図9と同じように考えます。

足し算をかけ算にする流れを式で表すと、こうなります。
$${(1+2+3)+(1+2+3)=3×4}$$
$${1+2+3=\frac{1}{2}×3×4}$$
・ 1+2+3+4=

足し算をかけ算にする流れを式で表すと、こうなります。
$${(1+2+3+4)+(1+2+3+4)=4×5}$$
$${1+2+3+4=\frac{1}{2}×4×5}$$
・ パターンを見つけて、公式を導く
$${1+2=\frac{1}{2}×2×3}$$
$${1+2+3=\frac{1}{2}×3×4}$$
$${1+2+3+4=\frac{1}{2}×4×5}$$
このように並べると、こんなパターンが分かります。
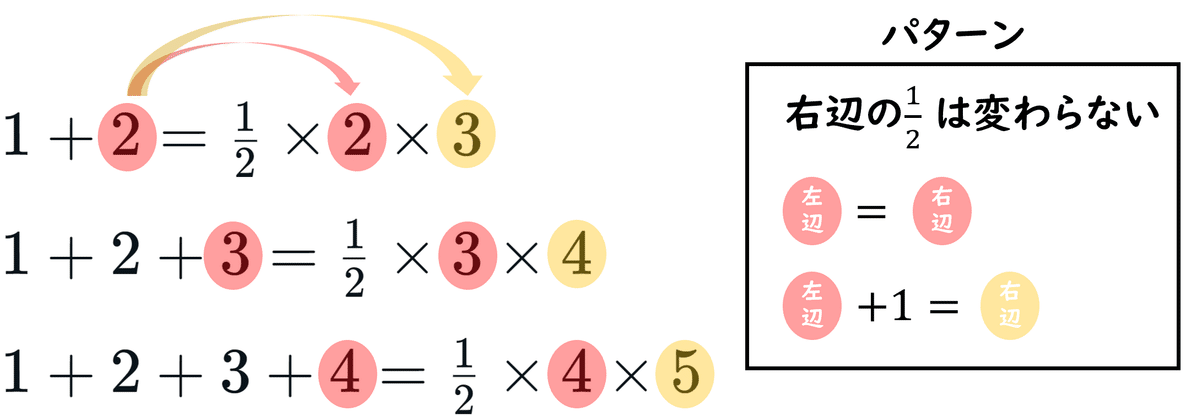
赤で囲んだ数は、上で示してきた三角形の底辺であり、長方形の短辺です。
オレンジで囲んだ数は、上で示してきた三角形の底辺と頂点の和であり、長方形の長辺です。
よって、次のような公式を導くことができます。
$${1+2+3+4+・・・+n=\frac{1}{2}n(n+1)}$$

5 公式が正しいことを、数式で示す
$${1+2+3+4}$$の図を、もう一度出します。

これを見ると、「1と4」、「2と3」、「3と2」、「4と1」の行を合わせているのが分かります。
こうすることで、全ての行の和が5になるというわけです。
では、$${1+2+3+・・・+n}$$だと、このような図です。

図14の三角形を使って平行四辺形を作ると、このようになります。

図15にあるペットボトルキャップの個数は、$${n(n+1)}$$個です。
図15の「各行のペットボトルキャップは$${n+1}$$個」の部分を補足します。
上から$${k}$$行目の白〇と下から$$[k}$$行目の色のついた〇同士で足すことは、これまでの図から明らかです。
白〇の三角形の上から$${k}$$行目の〇の数は$${k}$$個です。
色のついた〇の下から$${k}$$行目の〇の数$${n-(k-1)}$$個です。

上から$${k}$$行目の白〇と下から$$[k}$$行目の色のついた〇同士で足すと、
$${k+n-(k-1)=n+1}$$
なので、各行のペットボトルキャップは$${n+1}$$個といえます。
よって、
$${1+2+3+・・・+n=\frac{1}{2}n(n+1)}$$
といえます。
6 まとめ
公式を導くには、足し算をかけ算にすればよい。
足し算をかけ算にするということは、線の長さを求めることから面積を求めることに変わると捉えることができる。
$${1+2+3+・・・+n}$$の公式を導くには、まずペットボトルキャップを三角形に配置して、次に同じ形(合同)の三角形を180°回転させて右から付け加えて平行四辺形を作り、最後に平行四辺形を長方形に変形すればよい。
7 次回は
次回の記事では、
$${1^2+2^2+3^2+4^2・・・+n^2}$$
の公式を、今回の記事のまとめで書いたことを生かして求めていきます。
次の記事はこちら↓↓
最後まで読んでいただき、ありがとうございました!!

