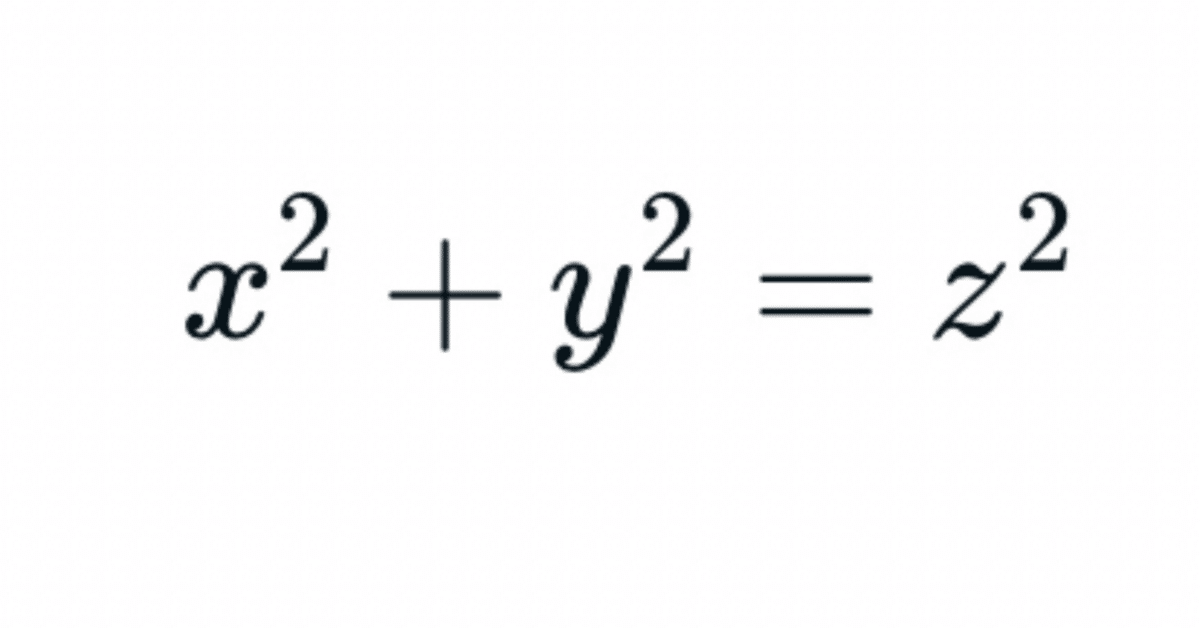
Mathematics short story #1
-------------------------------------------------
$${Published}$$ $${Online}$$ $${First}$$ $${(17/2/2024)}$$
$${Latest}$$ $${additions}$$ $${(17/2/2024)}$$
-------------------------------------------------
数学のどうでもいい小話シリーズ #1
まず
下記の等式を見てください
$${3^2=4~+~5}$$
$${3^2+4^2=5^2}$$
$${5^2=12~+~13}$$
$${5^2+12^2=13^2}$$
なんとも綺麗な等式だこと…
ほんとに合ってるの?という方は検算を…
この先も続きます
$${7^2=24~+~25}$$
$${7^2+24^2=25^2}$$
$${9^2=40~+~41}$$
$${9^2+40^2=41^2}$$
まぁこんな感じで続きます
規則性はなんとなくわかったけど
数学では証明しない事には上記の等式が
永遠に続くとは言えない
ではいきます
-------------------------------------------------
【証明】
まず最初の等式
$${3^2=4~+~5}$$
$${3^2+4^2=5^2}$$
を
$${x^2=y~+~z}$$
$${x^2+y^2=z^2}$$
とした時
この式の各$${x,y,z}$$の値を考えます
$${x=3,~5~,~7~,~9~,11,13,…}$$
$${y=4,12,24,40,60,84,…}$$
$${z=5,13,25,41,61,85,…}$$
ぱっとみたら
$${x}$$は奇数かな?
$${y,z}$$の差は$${1}$$?
には気付くと思います
自称「数学好き」にはこの様に見えています
まず
$${x}$$は初項$${3}$$ 公差$${2}$$の等差数列なので
等差数列の一般項の公式
初項$${a}$$ 公差$${d}$$の等差数列$${a_n}$$の一般項は
$${(}$$第$${n}$$項$${)=(}$$初項$${)+(n-1)×(}$$公差$${)}$$
つまり $${a_n=a+(n−1)d}$$
を使うと
$${x}$$の一般項$${x_n}$$は
$${x_n = 3+(n-1)×2 = 2n+1}$$
と求まります
(結局は奇数やん…😂)
次に
$${y}$$(階差数列)は公差が「初項$${8}$$ 公差$${4}$$の等差数列」になっているので
階差数列の一般項の公式
ある数列$${a_n}$$の階差数列$${b_n}$$を用いて数列$${a_n}$$の一般項は$${k \geqq2}$$の時
$${a_n=a_1+ \sum\limits_{k=1}^{n-1} b_k}$$
があるので
$${y}$$の階差数列$${w}$$の一般項をまず求めます
$${w}$$は「初項$${8}$$ 公差$${4}$$の等差数列」なのでその一般項$${w_n}$$は
$${w_n=8+(n-1)4=4n+4}$$
になるから$${y}$$の一般項$${y_n}$$は
$${y_n=y_1+ \sum\limits_{k=1}^{n-1} (4k+4)}$$
となる
ここで$${\sum}$$の和の公式
$${\sum\limits_{k=1}^n a = an}$$ $${~~(a}$$は定数$${)}$$
$${\sum\limits_{k=1}^n k = \dfrac{n(n+1)}{2}}$$
を用いると
$${\begin{aligned} y_n &=y_1+ \sum\limits_{k=2}^{n-1} (4k+4)\\&=4+2(n-1)n+4(n-1)\\&=2n^2+2n \end{aligned}}$$
$${z}$$はやっぱり$${y}$$より$${1}$$大きいから$${z}$$の一般項$${z_n}$$は
$${z_n=y_n+1}$$
つまり
$${z_n=2n^2+2n+1}$$
となる
これで全ての一般項が求まった
$${n \geqq1}$$のとき
$${x_n =2n+1}$$
$${y_n =2n^2+2n}$$
$${z_n =2n^2+2n+1}$$
はい証明終了🫣ではなくて…
まだです
$${x^2=y~+~z}$$
$${x^2+y^2=z^2}$$
に代入して確かめましょう
$${x^2=(2n+1)^2=4n^2+4n+1}$$
$${\begin{aligned} y+z &=(2n^2+2n)+(2n^2+2n+1)\\&=4n^2+4n+1\end{aligned}}$$
となり
$${x^2=y~+~z}$$
が成り立つ
更に
$${x^2=(2n+1)^2=4n^2+4n+1}$$
$${y^2=(2n^2+2n)^2=4n^4+8n^3+4n^2}$$
$${\begin{aligned}z^2 &=(2n^2+2n+1)^2\\&=4n^4+4n^2+1+8n^3+4n^2+4n\\&= 4n^4+8n^3+8n^2+4n+1\end{aligned}}$$
となり
$${x^2+y^2=z^2}$$
も成り立つ
【証明終】
-------------------------------------------------
ついでに
$${x^2=z^2-y^2=(z+y)(z-y)}$$
$${z-y=1}$$なら
$${x^2=z+y}$$
となるのは明白である
更に更に…
$${~5^2~=~4^2~+~3^2}$$
$${13^2=12^2+~5^2}$$
$${25^2=24^2+~7^2}$$
$${41^2=40^2+~9^2}$$
$${61^2=60^2+11^2}$$
左辺に注目すると
$${~5~=1^2+2^2}$$
$${13=2^2+3^2}$$
$${25=3^2+4^2}$$
$${41=4^2+5^2}$$
$${61=5^2+6^2}$$
これにも当然理由があります
$${z_n =2n^2+2n+1}$$
だったので…
$${z_n=n^2+(n+1)^2}$$
となります
う〜ん
綺麗ですなぁ…
キリがないので今日はおしまい
最後まで見て頂きありがとうございました😊
-------------------------------------------------
#2 へ
