【#04】材料力学の強化書 〜材料力学で利用する微分積分の復習〜

前回と同じくディズニーランドの城の写真です。今回は何かと話題になりました「美女と野獣」から。明確な城名はありませんが、外観のモデルはフランスにあるシャンボール城と言われています。

シャンボール城はレオナルド・ダ・ヴィンチが設計に関わったことで有名なお城で、世界遺産にも登録されています。いつか実際に見てみたいものです。

さて、材料力学の話を進めましょう。

前回は材料力学で扱う「変形」について、全部で５形態に分類できることを示しました。また、物体内部で引き起こされる内力については、全部で２形態に分類できることも示しました。

材料力学を進める上で前提となる話はここまで。今回は本題に入る前に、少しだけ寄り道をします。

以前に材料力学における物体は「連続体」として扱うと説明しました。これは、微分積分の導入が絶対であることを意味します。

微分積分は高校数学の中でも難易度の高い単元と言われていますが、材料力学で扱う範囲で説明するならば、決して高いハードルではありません。

今回は高校数学の復習を兼ねて、微分積分の話を必要最小限でまとめてみようと思います。

微分積分の復習

微分積分の理論的な説明は教科書に任せるとして、ここでは、イメージをつけることに注力します。

まずは言葉で説明すると、微分はある事象の微小（瞬間的）な変化を求めるものです。一方、積分はある事象の微小（瞬間的）な変化の積算を求めるものです。

例えば、車の移動について考えてみます。動くということは「位置」が変わり続けているとも言えます。この位置の情報がある関数で表されるとします。

距離の情報（ある時間にどの位置にいたか）が分かっていれば、特定の瞬間における速度を求められます。これが「微分」です。

また、速度の情報（ある瞬間にどのくらい位置が変化したか）が分かっていれば、特定の時間内に走行した距離を求められます。これが「積分」です。

今回は車の移動という具体的な事例を出しましたが、実際に用語を理解するのは上記のグラフの相互関係を追えている必要があるので、ここで確実に理解しておくようにしましょう。

※参考記事：微分積分について
https://univ-juken.com/bibun-sekibun

微分積分を適用する意味

改めて連続体の定義の確認をします。質点や剛体と連続体の違いは「変形」を扱えることにありました。

この「変形」について、もう少し細かく見てみます。工学では全体の変形状態を知るのは難しい場合に、任意の微小領域に切り分けてから全体を考えるというプロセスを辿ることが一般的です。

例えば、下記のようなテーパー棒の変形を考える場合について。まずは棒の長手方向（ｘ方向）に対する断面を微小領域と仮定して変形を考えます。微小領域に切り分けることで、問題を簡単にすることがポイントです。

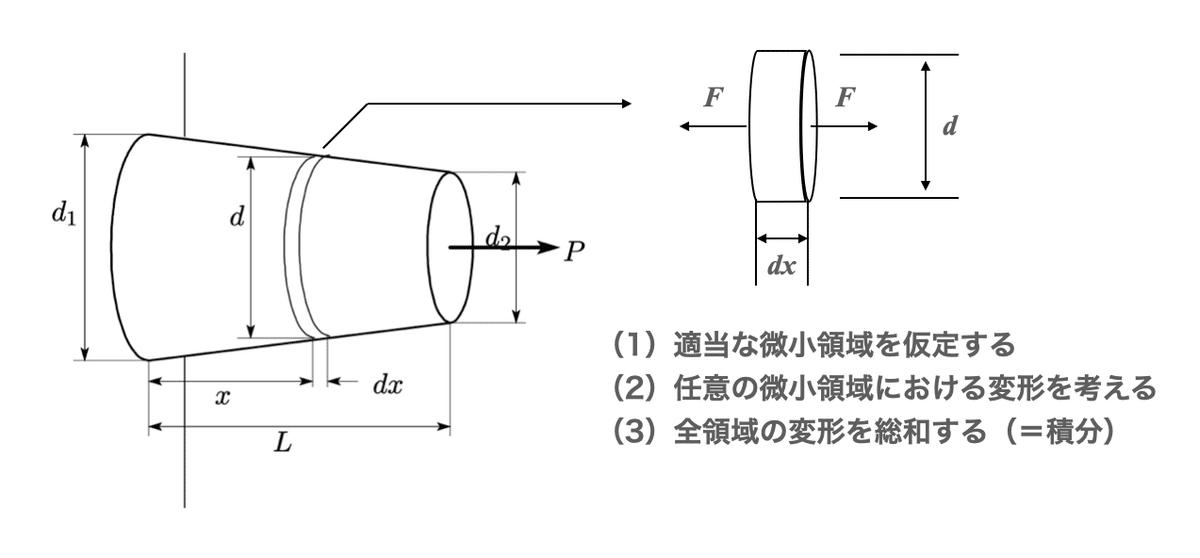
この微小領域での変形を捉えたならば、それを全ての断面に対して適用します。ここで登場するのが積分法になります。微小領域での結果を用いて、全体の変形を手計算で一気に求めるのです。

具体的な計算については後ほど進めます。まずは積分という作業を行う理由を後述と合わせて理解して頂けたらと思います。

微分積分の公式（必須事項）

材料力学で扱う微分積分の公式ですが、実はべき乗関数のケースくらいです。下記にまとめます。ここで、ｎは実数、Ｃは積分定数です。

$${\dfrac{d}{dx}(x^n)=nx^{n-1}}$$   $${(n\neq0)}$$

$${\displaystyle \int{x^n}dx=\frac{1}{n+1}x^{n+1}+C}$$   $${(n\neq-1)}$$

より複雑な形状になる場合は上記以外の公式を使うことがありますが、基本的に上記の公式を覚えておけば問題は無いと思います。

おわりに

今回は少し寄り道をして、微分積分の復習と材料力学での使い方について説明しました。

工学で用いる微分積分の知識は、沢山の公式を知っているかというよりも、如何にして活用するかという観点に集約されると思います。そのため、公式の話ではなくイメージを付けて頂くことに注力しました。

今回はあくまで寄り道として扱いましたが、ここできちんと復習をしておいて頂けたらと思います。

-------------------------

最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに添えるように頑張ります。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎