東京理科大学 創域理工学部 2025/2/3 数学 大問2 解答 解説

こんにちは、Uraと申します。
予備校講師やプロ家庭教師として、小中高生を第一志望合格に導くべく活動している者です。

本記事は、つい昨日行われた「理科大 創域理工学部」の入試で出題された「数学 大問2」を解説していきます。

Threadsでも呟きましたが，基礎的な出題が多い創域理工学部の数学の大問として，過去最難レベルだったと思います。

試験会場で解いてよくわからなかったから解説を確認したい方，来年以降の受験生で理科大の数学に挑戦してみたい方，ぜひ取り組んでみてください。

■問題

$${e}$$を自然対数の底とし，$${\log}$$は自然対数とする。
座標平面上の曲線$${y=e^x}$$を$${C_1}$$とする。実数$${t}$$に対し，$${C_1}$$上の点を$${P(t,e^t)}$$とする。

以下の条件(a)，(b)，(c)を満たす円を$${C_2}$$とする。

（a）円の中心$${Q(X,Y)}$$は$${0＜Y＜e^X}$$を満たす。
（b）円$${C_2}$$は$${x}$$軸と接する。
（c）点Pは円$${C_2}$$上にあり，点Pにおいて$${C_1}$$と$${C_2}$$は共通の接線$${l}$$をもつ。

次の問いに答えよ。

（1）接線$${l}$$の方程式を，$${t}$$を用いて表せ。
（2）$${k}$$と$${m}$$は実数で，$${k}$$は正であり，ベクトル$${k(m,-1)}$$は接線$${l}$$に垂直な単位ベクトルである。$${k}$$と$${m}$$を，$${t}$$を用いて表せ。
（3）円$${C_2}$$の面積を$${S}$$とおく。極限$${\lim_{t\to -\infty} \frac{S}{X-t}}$$を求めよ。（$${S}$$と$${X}$$は$${t}$$の関数である。）

以下，$${t=\frac{1}{2}\log3}$$とする。（このとき，円$${C_2}$$は$${x≧0，y≧0}$$の範囲に含まれている。このことは示さなくてよい。）
円$${C_2}$$と$${x}$$軸との接点をRとし，円$${C_2}$$の2点P，Rを結ぶ弧のうち短い方を$${C_3}$$とする。

（4）弧$${C_3}$$の中心角∠PQRを求めよ。
（5）$${x}$$軸，$${y}$$軸，曲線$${C_1}$$，および，弧$${C_3}$$で囲まれた部分の面積を求めよ。

■解答 解説

まずは図を描いて状況の確認。

（1）接線の方程式

（2）法線ベクトル

法線ベクトルについて，参考書には

直線$${ax+by+c=0}$$の法線ベクトルは$${(a,b)}$$

などと載っていることが多いと思います。もちろんそれを使ってもよいですが，「それを知らなかったらこのように解く」という解説にしています（根本的には同じ話で，上の事実の導出に近いものになります）

（3）極限

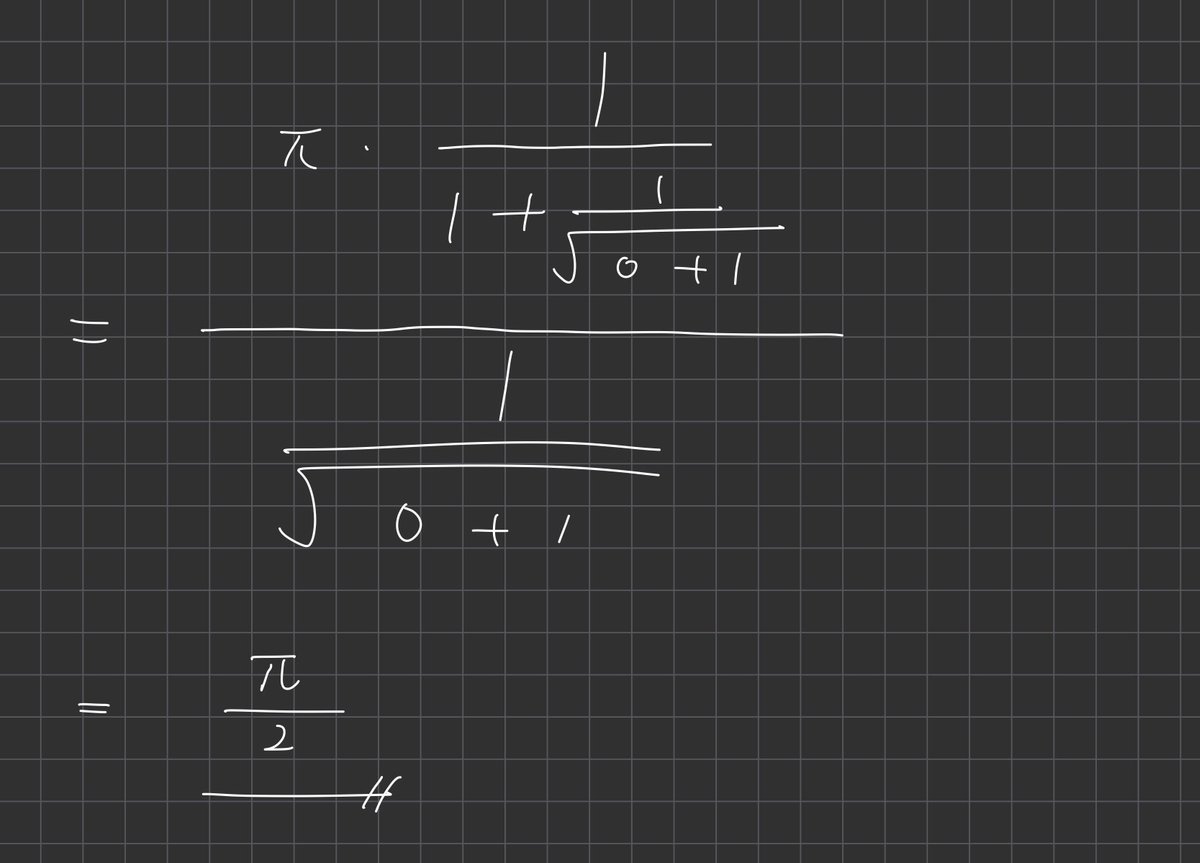
（4）中心角

（5）面積

■合格点を取る上でのポイント

私は過去問をすべて解いていますが，創域理工学部の数学の大問として過去最難レベルだったと思います。
創域理工学部の数学では基本的・標準的な出題が多いので，過去問演習をしっかり積んでいた受験生ほど面食らったのではないでしょうか。

本記事執筆時点ではまだ合格最低点などが不明ですが，合格を勝ち取る上でこの大問を完答する必要がないのは確かです。

問題文の次の太字の部分などを読んで，作問者も難易度調整には苦心したのかなと推測しました（太字部分がないとさらに面倒な問題になります）

────────────────────

以下，$${t=\frac{1}{2}\log}$$とする。（このとき，円$${C_2}$$は$${x≧0，y≧0}$$の範囲に含まれている。このことは示さなくてよい。）

以下，小問ごとに見ていきます。

（1）は絶対に落とせない問題。

続く（2）が難所で，（2）を使う（3）も同様。
さらに（3）が（5）に繋がるので，（2）が解けないと実質的に小問3個を落とす構成。
ただし，この3個を落とすことは合格を掴む上で問題ありません。

差がつきそうなのは，（2）が解けなくても諦めずに（4）を見れたかということ。（4）は（1）が出来ていれば戦える問題ですので，ここを拾えた受験生は合格にかなり近づけたと思います。

大問途中の小問で詰まったとき，直ちに残りの小問を捨てるのか，残りの小問で解ける問題がないかをしっかり確認するのか。
この試験に限らず分岐点になりますので，後者を徹底してみてください。

---

以上、
東京理科大学 創域理工学部 2025/2/3 数学 大問2
を解説してきました。いかがでしたでしょうか。

私は現在家庭教師のご依頼を受け付けております。私は数学、英語、物理のすべてを教えることができるので、理科大志望の生徒さまを総合的に導くことができます。

例えば「合格まであと20点」という状況の生徒さまに対し、数学講師としてキャリアをスタートした当時の私は数学の伸ばし方を伝えることしかできませんでしたが、今では「どの科目でその20点を取りに行くのが最適解か」を示すことができます。

下の記事から体験授業（オンラインであれば無料）も受け付けておりますのでぜひご連絡ください。ご相談だけでも大歓迎です。

あなたの受験がより良いものになることを心から祈っております。
それでは！

Ura