
3次方程式の解の公式の存在を「可解群」で証明する
前回の本シリーズ (36) で、2次方程式について「(累乗根の添加による)体の拡大」と「(巡回群をともなう)群の縮小」との対応、つまりガロア対応を解説しました。ここでは3次方程式についてのガロア対応を解説し、3次方程式に解の公式が存在することを証明していきます。
まずは、重要項目について復習していきます。
(復習)可解群について
2次方程式についてのガロア対応は次のようになります(本シリーズ (36))。
$$
\begin{align*}
&\hspace{-10pt}{\footnotesize X_2 を添加}\\[-3pt]
&\hspace{4pt}\downarrow\\
{\small \bm{<体の拡大>}}\hspace{8pt}Q_2&\hspace{-1pt}\overset{\bm{拡大}}{\subset} Q_2(X_2)\\
\Updownarrow{\scriptsize \bm{対応}}\hspace{-15pt}&\hspace{25pt}\Updownarrow {\scriptsize \bm{対応}}\\
{\small \bm{<群の縮小>}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI, \tau I\} \atop が巡回群}
\end{align*}
$$
解の差積
$${X_2=\alpha-\beta}$$
の添加は平方根の添加に相当します(本シリーズ (21) 他)。剰余類の集合 $${\{id I, \tau I\}}$$ が、ただの群(剰余群)ではなく巡回群になることが重要です。巡回群でなければガロア対応になりません。
また、本章で詳しく解説しますが、3次方程式についてのガロア対応は次のようになります。
$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_3 を添加}\hspace{8pt}{\footnotesize A を添加}\\[-4pt]
&\hspace{17pt}\downarrow\hspace{37pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\[-3pt]
&\hspace{17pt}\Updownarrow\hspace{7pt}{\footnotesize 対応}\hspace{7pt}\Updownarrow\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN, \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI, \rho_2I, \rho_3I\} \atop が巡回群}
\end{align*}
$$
$${Q_3(\omega)}$$ を基礎体とし、解の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
の添加は平方恨の添加に相当します(本シリーズ (12))。またラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
の添加は3乗根の添加に相当します(本シリーズ (13))。そして、3乗根まで添加された拡大体 $${Q_3(\omega, X_3, A)}$$ 内で、3次方程式の解の公式は構成(導出)可能となります。

解の公式が存在するかどうかは、このガロア対応の「群の構造」を調べればよいことを前回の章で解説しました。
2次方程式については
$$
\begin{align*}
{\small \bm{<群の縮小>}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I} \cdots (*1)\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI, \tau I\} \atop が巡回群}
\end{align*}
$$
3次方程式については
$$
\begin{align*}
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I} \cdots (*2)\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN, \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI, \rho_2I, \rho_3I\} \atop が巡回群}
\end{align*}
$$
となる群の構造です。
この $${(*1), (*2)}$$ のような、正規部分群による剰余類の集合(剰余群)が巡回群となるルールを保ちながら
「 $${I=\{id\}}$$ へといたる正規部分群の縮小の列」
をもつ群のことを『可解群』といいます(本シリーズ (36))。
解の公式が存在するかどうかは、2次対称群 $${S_2}$$ や3次対称群 $${S_3}$$ などが、可解群であるかどうかによります。つまり
$${S_2}$$ は可解群となるので、2次方程式に解の公式が存在する。
$${S_3}$$ は可解群となるので、3次方程式に解の公式が存在する。
ということです。2次方程式については前回の章でやったので、ここでは3次方程式について解説していきます。
3次方程式の解の公式が存在する理由について、解の差積 $${X_3}$$ とラグランジュ・リゾルベント $${A}$$ が関係しています(本シリーズ (26) 他)。
まずは復習として、差積 $${X_3}$$ とラグランジュ・リゾルベント $${A}$$ に3次置換を作用させることによって、式を変化させない置換が
「3次置換 $${\rightarrow}$$ 遇置換 $${\rightarrow}$$ 恒等置換」
と縮小されていく過程をみていきます。
そして、この置換が縮小されていく過程を「体の拡大」と「群の縮小」に関連付けることによって $${S_3}$$ は可解群となること、つまり3次方程式に解の公式が存在することを解説していきます。
中盤に「体」が出てくるところまでは、おもに本シリーズ (6)~(10) の復習です。3次置換を作用させる計算が長く続くので、分かっている場合は(復習)の部分を読み飛ばしてもかまいません。
まずは、3次置換について復習します。
(復習)3次置換について
3次置換とは、3つの文字 $${\alpha, \beta, \gamma}$$ の入れ替えのことで、次の6種類があります(本シリーズ (6))。この3つの文字を3次方程式の解とすれば、それは3次方程式の3つの解の置換となります。
$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha \beta \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$
置換は上から下へと置き換えると読みます。つまり
$$
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
$$
は、$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換です。これは
$${\alpha \rightarrow \gamma \rightarrow \beta \rightarrow \alpha \rightarrow \gamma \rightarrow \beta \rightarrow \alpha \rightarrow \cdots}$$
と3つの文字を巡回的に置き換える置換なので、これを3次巡回置換といい
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)
$$
と表記します(本シリーズ (14))。
また
$$
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
$$
は、$${\alpha}$$ はそのままで、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換です。これは、$${\beta}$$ と $${\gamma}$$ を入れ替える置換なので、これを互換といい
$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$
と表記します(本シリーズ (8))。互換は
$${\beta \rightarrow \gamma \rightarrow \beta \rightarrow \gamma \rightarrow \beta \rightarrow \cdots}$$
と2つの文字の巡回置換、つまり2次巡回置換とみることもできます。
ここで、便宜上3次置換を次のように
$${id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3}$$
と置きます。
$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=id\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)=\rho_2\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha \beta \gamma)=\rho_3
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}=\tau_1\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}=\tau_2\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}=\tau_3
\end{rcases}奇置換
\end{align*}
$$
(復習)3次置換の作用による差積の変化
ここで、3次方程式 $${ax^3+bx^2+cx+d=0}$$ の3つの解を $${\alpha, \beta, \gamma}$$ とします。すると、この3次方程式の3つの解の差積は
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
となります。
なお、これまでは、一般の3次方程式 $${ax^3+bx^2+cx+d=0}$$ をチルンハウス変換させた、$${y^3+py+q=0}$$ の3つの解を $${\alpha, \beta, \gamma}$$ と置きました(本シリーズ (6))。
チルンハウス変換とは、式をよりシンプルに変形する計算方法です。次のように、3次方程式の $${x_2}$$ の項が消えます(本シリーズ (3)、(25))。
$$
\begin{align*}
ax^3+bx^2+cx+d&=0\\
&\hspace{-20pt}\downarrow \Leftarrow {\footnotesize x=y-\dfrac{b}{3a} とおく \atop(チルンハウス変換)}\\
y^3+py+q&=0
\end{align*}
$$
チルンハウス変換は、あくまでも3次方程式の解の公式を導出するための1つのテクニックなので、群の構造(解の置換の構造)を考察する上で本質的に必要なものではありません(注1)。
よって、これからやる3次置換
$${id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3}$$
は、(チルンハウス変換された $${x^3+px+q=0}$$ の解ではなく)一般の3次方程式 $${ax^3+bx^2+cx+d=0}$$ の3つの解 $${\alpha, \beta, \gamma}$$ の置換です。
差積に3次置換を作用させる
ここで、3次方程式 $${ax^3+bx^2+cx+d=0}$$ の3つの解 $${\alpha, \beta, \gamma}$$ について、その解の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
に3次置換を作用させていきます。本シリーズ (9) の復習です。
$${➀}$$ $${\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}=id}$$ を作用させる
同じ文字同士を置き換える置換なので変化しません。
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{15.5pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow\hspace{8pt}\downarrow\hspace{13pt}\downarrow {\small 置き換え}\\
&\hspace{-1pt}\rightarrow\hspace{-1pt}(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=X_3 \Rightarrow 変化しない
\end{align*}
$$
$${➁}$$ $${\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}=\rho_2}$$ を作用させる
$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{15.5pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow\hspace{9pt}\downarrow\hspace{13pt}\downarrow {\small 置き換え}\\
&\hspace{-1pt}\rightarrow\hspace{-1pt}(\gamma-\alpha)(\alpha-\beta)(\beta-\gamma)\\
&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=X_3 \Rightarrow 変化しない
\end{align*}
$$
カッコ ( ) の順番が入れ替わるだけなので、もとの式と変わりません。
$${➂}$$ $${\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}=\rho_3}$$ を作用させる
$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{15.5pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow \hspace{9pt}\downarrow\hspace{13pt}\downarrow {\small 置き換え}\\
&\hspace{-1pt}\rightarrow\hspace{-1pt}(\beta-\gamma)(\gamma-\alpha)(\alpha-\beta)\\
&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=X_3 \Rightarrow 変化しない
\end{align*}
$$
これも、カッコ ( ) の順番が入れ替わるだけなので、もとの式と変わりません。
$${➃}$$ $${\dbinom{\alpha \beta \gamma}{\alpha \gamma \beta}=\tau_1}$$ を作用させる
$${\alpha}$$ はそのままで、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換なので
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{33.5pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow\hspace{9pt}\downarrow {\small 置き換え}\\
&\hspace{-1pt}\rightarrow\hspace{-1pt}(\underline{\alpha-\gamma})(\gamma-\beta)(\underline{\underline{\beta-\alpha}})\\
&=(\underline{\underline{\beta-\alpha}})(\gamma-\beta)(\underline{\alpha-\gamma}) \Leftarrow ( ) を入れ替えた\\
&=(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
&=\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
&=(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=-X_3 \Rightarrow -1 倍と変化する
\end{align*}
$$
この場合は $${-1}$$ 倍に変化します。
$${➄}$$ $${\dbinom{\alpha \beta \gamma}{\gamma \beta \alpha}=\tau_2}$$ を作用させる
$${\beta}$$ はそのままで、$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{16pt}\downarrow\hspace{46pt}\downarrow\hspace{8pt}\downarrow\hspace{14pt}\downarrow {\small 置き換え}\\
&\rightarrow(\underline{\gamma-\beta})(\underline{\underline{\beta-\alpha}})(\alpha-\gamma)\\
&=(\underline{\underline{\beta-\alpha}})(\underline{\gamma-\beta})(\alpha-\gamma) \Leftarrow ( ) を入れ替えた\\
&=(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
&=\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
&=(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=-X_3 \Rightarrow -1 倍と変化する
\end{align*}
$$
この場合も $${-1}$$ 倍に変化します。
$${➅}$$ $${\dbinom{\alpha \beta \gamma}{\beta \alpha \gamma}=\tau_3}$$ を作用させる
$${\gamma}$$ はそのままで、$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{15.5pt}\downarrow\hspace{14pt}\downarrow\hspace{8pt}\downarrow\hspace{46pt}\downarrow {\small 置き換え}\\
&\hspace{-1pt}\rightarrow\hspace{-1pt}(\beta-\alpha)(\underline{\alpha-\gamma})(\underline{\underline{\gamma-\beta}})\\
&=(\beta-\alpha)(\underline{\underline{\gamma-\beta}})(\underline{\alpha-\gamma}) \Leftarrow ( ) を入れ替えた\\
&=(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
&=\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
&=(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=-X_3 \Rightarrow -1 倍と変化する
\end{align*}
$$
この場合も $${-1}$$ 倍に変化します。
以上をまとめると、$${➀}$$~$${➂}$$ の遇置換では $${X_3}$$ は変化しません。
$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}=id\\
\\
➁\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}=\rho_2\\
\\
➂\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}=\rho_3
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\rightarrow (\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&=X_3\\
&\Rightarrow \boldsymbol{\small 変化しない}
\end{align*}
$$
一方、$${➃}$$~$${➅}$$ の奇置換では $${X_3}$$ は $${-1}$$ 倍に変化します。
$$
\begin{rcases}
➃\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}=\tau_1\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}=\tau_2\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}=\tau_3
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\rightarrow -(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&=-X_3\\
&\Rightarrow \boldsymbol{\small -1 倍に変化する}
\end{align*}
$$
この結果を対称性という観点でとらえると、$${X_3}$$ は遇置換では変化しません。しかし奇置換では変化するので、遇置換のみで対称性を保ちます。これを、群置換シンメトリーという言葉で表します。$${X_3}$$ は遇置換シンメトリーをもっています。
$$
\begin{align*}
X_3 &\Rightarrow 変化しないのは遇置換のみ\\
&\Rightarrow \bm{遇置換シンメトリー}をもつ
\end{align*}
$$
差積の2乗に3次置換を作用させる
では次に、差積の2乗
$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
に $${➀}$$~$${➅}$$ の3次置換を作用させましょう。それには、先ほどの $${X_3}$$ の結果を利用します。
$${➀}$$~$${➂}$$ は、もともと変化しないので2乗しても変化しません
$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}=id\\
\\
➁\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}=\rho_2\\
\\
➂\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}=\rho_3
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
(X_3)^2&=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\rightarrow\!\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&=(X_3)^2\\
&\Rightarrow\boldsymbol{\small 変化しない}
\end{align*}
$$
$${➃}$$~$${➅}$$ は、$${-1}$$ 倍の $${2}$$ 乗は $${1}$$ 倍なので変化しません。
$$
\begin{rcases}
➃\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}=\tau_1\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}=\tau_2\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}=\tau_3
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
(X_3)^2&=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\rightarrow\!\{-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&=(-1)^2\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&=(X_3)^2\\
&\Rightarrow\boldsymbol{\small 変化しない}
\end{align*}
$$
すなわち、$${➀}$$~$${➅}$$ のすべての3次置換を作用させても変化しないので
$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
は対称式となります。
$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}=id\\
\\
➁\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}=\rho_2\\
\\
➂\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}=\rho_3\\
\\
➃\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}=\tau_1\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}=\tau_2\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}=\tau_3
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
(X_3)^2&={\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2\\
&\rightarrow {\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2\\
&=(X_3)^2\\
&\Rightarrow\boldsymbol{\small 変化しない}\\
&\Rightarrow\boldsymbol{\small 対称式}
\end{align*}
$$
対称性が遇置換シンメトリーに破壊されたこと
これまでの結果を対称性という観点でとらえると
$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
は対称式ですが、その平方根をとった解の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
そのものについては、式を変化させない置換は遇置換のみです。$${(X_3)^2}$$ から $${X_3}$$ にかけて、対称性は3次置換(対称式)から遇置換シンメトリニーに破壊されています。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&(X_3)^2\\
{\small 平方根を取る}\downarrow\hspace{-13pt}&\\
&\hspace{5pt}X_3\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[-5pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&3次置換 id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)}}\\
&遇置換 id, \rho_2, \rho_3\\
\end{align*}
\end{align*}
$$
何次方程式でも解の差積をつくることはできるので、最初に差積を与えることは、初めに対称性を破壊する上での常套手段となります(本シリーズ (21))。
(注)
なお、本シリーズでは、式を変化させない置換が縮小されていく過程を「対称性が絞られる」、「対称性が崩れる」または「対称性が壊れる」と複数の表現を用いて書いてきました。
ここからは、式を変化させない置換が縮小されていく過程を「対称性の破壊」という文言で統一していきます。「破壊」という言葉は、いろいろな参考書でも用いられているようです(分かりにくければ、遡って修正する予定です)。
また、$${(X_3)^2}$$ の平方根は $${X_3, -X_3}$$ の2つあることを注意しておきます。$${(X_3)^2}$$ の平方根とは2乗して $${(X_3)^2}$$ になるものなので、 $${X_3, -X_3}$$ の2つになります。
$${X_3}$$ の2乗は $${(X_3)^2}$$
$${-X_3}$$ の2乗は $${(-X_3)^2=(X_3)^2}$$
ここでは簡単のため、係数がプラスの $${X_3}$$ を採用しています。
(注)終わり
アーベルの証明でもやりましたが、次々と累乗根を添加することにより、式を変化させない置換を最終的に $${id}$$ まで破壊することが、解の公式の存在を保証する上で重要になります。2次方程式の解の公式でも、 $${id}$$ への対称性の破壊がみられました(本シリーズ (20))。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&(X_2)^2\\
{\small 平方根を取る}\downarrow\hspace{-13pt}&\\
&\hspace{5pt}X_2\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[-5pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&2次置換 id, \tau\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)}}\\
&恒等置換 id\\
\end{align*}
\end{align*}
$$
式を変えない置換を $${id}$$ まで破壊する理由は、$${\alpha}$$ は $${\alpha}$$ のまま、$${\beta}$$ は $${\beta}$$ のまま、$${\gamma}$$ は $${\gamma}$$ のままと、1文字の式 $${\alpha, \beta, \gamma}$$ を変化させない置換は、恒等置換 $${id}$$ のみだからです。
$$
\begin{align*}
&3次置換 id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)}}\\
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\downarrow\\
&\hspace{14pt}\vdots {\small \bm{置換の縮小(対称性の破壊)}}\\
&\hspace{10pt}\downarrow\\
&恒等置換 id(目標)
\end{align*}
$$
さて、3次対称群は遇置換まで破壊されました。ここからさらに、何か都合のよい式を与えることによって、さらに対称性を破壊していきます。その都合のよい式がラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
です。
ここから、$${A^3}$$ は遇置換で変化しない(遇置換シンメトリーをもつ)が、その3乗根である $${A}$$ そのものは、変化させない置換は恒等置換 $${id}$$ のみであることを解説していきます。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&\hspace{6pt}A^3\\
{\small \bm{3乗根を取る}}\downarrow\hspace{-13pt}&\\
&\hspace{6pt}A\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[-5pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)}}\\
&恒等置換 id\\
\end{align*}
\end{align*}
$$
(注)$${A^3}$$ の3乗根は $${A, \omega A, \omega^2A}$$ の3つあることを注意しておきます。$${A^3}$$ の3乗根とは3乗して $${A^3}$$ になるものなので、 $${A, \omega A, \omega^2A}$$ の3つになります。
$${\hspace{11pt}A}$$ の3乗は $${A^3}$$
$${\hspace{4pt}\omega A}$$ の3乗は $${(\omega A)^3=\underset{1}{\underline{\omega^3}}A^3=A^3}$$
$${\omega^2 A}$$ の3乗は $${(\omega^2 A)^3={(\omega^2)}^3 A^3=\underset{1}{\underline{\omega^6}}A^3=A^3}$$
ここでは簡単のため、係数が $${1}$$ の $${A}$$ を採用しています。
なお、$${\omega}$$ は3乗して $${1}$$ になる数($${1}$$ の3乗根)のうち虚数であるものなので
$${\omega^3=1}$$
$${\omega^6=(\underset{1}{\underline{\omega^3}})^2=1^2=1}$$
です(本シリーズ (24))。
(復習)遇置換の作用によるラグランジュ・リゾルベントの変化
ラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
に、遇置換 $${id, \rho_2, \rho_3}$$ を作用させていきます(本シリーズ(6))。すでに群置換シンメトリーまで対称性は破壊されたので、奇置換は考えないで遇置換のみを考えます。
なお、ラグランジュリゾルベントには、もう一つ
$${B=\alpha+\omega^2\beta+\omega\gamma}$$
もあります。$${\beta}$$ と $${\gamma}$$ の係数が $${A}$$ と $${B}$$ で入れ替わっています。
$$
\begin{alignat*}{2}
A=\alpha+&\omega\beta+& &\omega^2\gamma\\
{\small 入れ替わる}\hspace{3pt}&\hspace{-2pt}\updownarrow & &\hspace{-2pt}\updownarrow {\small入れ替わる}\\
B=\alpha+&\omega^2\beta+& &\omega\gamma
\end{alignat*}
$$
$${A}$$ と $${B}$$ は相互に関係があるので、比較のため $${B}$$ についても遇置換を作用させていきます。
また、$${\omega}$$ について次の公式を利用します。
$$
\begin{align*}
\omega^3=1
\end{align*}
$$
$${\omega}$$ は3乗して $${1}$$ になる数($${1}$$ の3乗根)のうち、虚数であるものです(本シリーズ (24))。
ラグランジュ・リゾルベント A, B に遇置換を作用させる
$${➀}$$ $${\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}=id}$$ を作用させる。
$${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に、$${\gamma}$$ を $${\gamma}$$ に置き換える置換なので
$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow {\small 置き換え}\\
&\alpha+\omega\beta+\omega^2\gamma=A \Rightarrow {\small 変化しない}\\
\\
B=\,&\alpha+\omega^2\beta+\omega\gamma\\
&\hspace{-2pt}\downarrow\hspace{24pt}\downarrow\hspace{20pt}\downarrow {\small 置き換え}\\
&\alpha+\omega^2\beta+\omega\gamma=B \Rightarrow {\small 変化しない}\\
\end{align*}
$$
$${➀}$$ は恒等置換なので $${A}$$ は $${A}$$ のまま、$${B}$$ は $${B}$$ のままで変わりません。
$${➁}$$ $${\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}=\rho_2}$$ を作用させる
$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow {\small 置き換え}\\
&\gamma+\omega\alpha+\omega^2\beta\\
=\,&\underset{1}{\underline{\omega^3}}\,\gamma+\omega\alpha+\omega^2\beta\\
=\,&\omega(\omega^2\gamma+\alpha+\omega\beta)\\
=\,&\omega(\alpha+\omega\beta+\omega^2\gamma)=\omega A \Rightarrow {\small \omega 倍に変化}\\
\\
B=\,&\alpha+\omega^2\beta+\omega\gamma\\
&\hspace{-2pt}\downarrow\hspace{24pt}\downarrow\hspace{20pt}\downarrow {\small 置き換え}\\
&\gamma+\omega^2\alpha+\omega\beta\\
=\,&\underset{1}{\underline{\omega^3}}\,\gamma+\omega^2\alpha+\underset{1}{\underline{\omega^3}}\cdot\omega\beta\\
=\,&\omega^3\gamma+\omega^2\alpha+\omega^4\beta\\
=\,&\omega^2(\omega\gamma+\alpha+\omega^2\beta)\\
=\,&\omega^2(\alpha+\omega^2\beta+\omega\gamma)=\omega^2B \Rightarrow {\small \omega^2 倍に変化}
\end{align*}
$$
$${➁}$$ の置換では $${A}$$ は $${\omega A}$$ に、$${B}$$ は $${\omega^2B}$$ に変化します。
ポイントは、所々で $${\omega^3=1}$$ をうまく使います。
$${A}$$では $${\gamma}$$ に $${\omega^3(=1)}$$ をかけます。
$${B}$$では $${\gamma}$$ と $${\omega\beta}$$ の2か所に $${\omega^3(=1)}$$ をかけます。$${\omega^3}$$ は $${1}$$ なので、かけても式の値は変わりません。また、
$${A}$$ では最後に $${\omega}$$ でくくって $${\omega A}$$ を導きます。
$${B}$$ では最後に $${\omega^2}$$ でくくって$${\omega^2B}$$ を導きます。くくったときに、$${\alpha}$$ の係数がともに $${1}$$ になるのがポイントです。
$${➂}$$ $${\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}=\rho_3}$$ を作用させる
$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow {\small 置き換え}\\
&\beta+\omega\gamma+\omega^2\alpha\\
=\,&\underset{1}{\underline{\omega^3}}\,\beta+\underset{1}{\underline{\omega^3}}\cdot\omega\gamma+\omega^2\alpha\\
=\,&\omega^3\beta+\omega^4\gamma+\omega^2\alpha\\
=\,&\omega^2(\omega\beta+\omega^2\gamma+\alpha)\\
=\,&\omega^2(\alpha+\omega\beta+\omega^2\gamma)=\omega^2A \Rightarrow {\small \omega^2 倍に変化}\\
\\
B=\,&\alpha+\omega^2\beta+\omega\gamma\\
&\hspace{-2pt}\downarrow\hspace{24pt}\downarrow\hspace{20pt}\downarrow {\small 置き換え}\\
&\beta+\omega^2\gamma+\omega\alpha\\
=\,&\underset{1}{\underline{\omega^3}}\,\beta+\omega^2\gamma+\omega\alpha\\
=\,&\omega(\omega^2\beta+\omega\gamma+\alpha)\\
=\,&\omega(\alpha+\omega^2\beta+\omega\gamma)=\omega B \Rightarrow {\small \omega 倍に変化}
\end{align*}
$$
$${➂}$$ の置換では $${A}$$ は $${\omega^2 A}$$ に、$${B}$$ は $${\omega B}$$ に変化します。
ここでも所々で $${\omega^3=1}$$ を使います。
$${A}$$ では最後に $${\omega^2}$$ でくくって $${\omega^2A}$$ を導き、$${B}$$ では最後に $${\omega}$$ でくくって$${\omega B}$$ を導きます。くくったときに、$${\alpha}$$ の係数がともに $${1}$$ になるのがポイントです。
以上をまとめると
$$
\hspace{-10pt}
\begin{align*}
&➀
\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}=id
\hspace{7pt}
では
\hspace{12pt}
\begin{align*}
A &\longrightarrow A\\
B &\longrightarrow B
\end{align*}\\
&②
\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}=\rho_2
\hspace{7pt}
では
\hspace{12pt}
\begin{align*}
A &\longrightarrow \omega A\\
B &\longrightarrow \omega^2 B
\end{align*}\\
&③
\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}=\rho_3
\hspace{7pt}
では
\hspace{12pt}
\begin{align*}
A &\longrightarrow \omega^2 A\\
B &\longrightarrow \omega B
\end{align*}
\end{align*}
$$
すると、ラグランジュ・リゾルベント $${A, B}$$ を変化させない置換は恒等置換 $${id}$$ のみです。恒等置換以外ではラグランジュ・リゾルベントは変化します。
ラグランジュ・リゾルベントの3乗に遇置換を作用させる
次に、ラグランジュ・リゾルベントの3乗 $${A^3, B^3}$$ に遇置換 $${id, \rho_2, \rho_3}$$ を作用させます。それには、先ほどやった $${A, B}$$ の結果をそのまま利用します。
なお、$${\omega}$$ について次の公式を利用します。$${\omega}$$ は3乗して $${1}$$ になる数($${1}$$ の3乗根)のうち、虚数であるものです。
$$
\begin{align*}
\omega^3&=1\\
\omega^6&=(\underset{1}{\underline{\omega^3}})^2=1^2=1
\end{align*}
$$
すると、$${A^3}$$ と$${B^3}$$ の遇置換による行き先は
$$
\begin{align*}
&\begin{alignat*}{2}
&➀\hspace{5pt}\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}=id\hspace{5pt}では & A^3&\rightarrow A^3\\
& & B^3&\rightarrow B^3
\end{alignat*}\\
\\
&\begin{alignat*}{2}
&②\hspace{5pt}\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}=\rho_2\hspace{5pt}では & A^3\rightarrow &\,(\omega A)^3\\[-4pt]
& & =&\,\,\underset{1}{\underline{\omega^3}}A^3\\
& & =&\,1\cdot A^3=A^3\\[5pt]
& & B^3\rightarrow&\,(\omega^2B)^3\\
& & =&\,\,(\omega^2)^3B^3\\
& & =&\,\,\underset{1}{\underline{\omega^6}}B^3\\
& & =&\,\,1\cdot B^3=B^3
\end{alignat*}\\
\\
&\begin{alignat*}{2}
&③\hspace{5pt}\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}=\rho_3\hspace{5pt}では & A^3\rightarrow&\,(\omega^2 A)^3\\[-4pt]
& & =&\,\,(\omega^2)^3A^3\\
& & =&\,\,\underset{1}{\underline{\omega^6}}A^3\\
& & =&\,\,1\cdot A^3=A^3\\[5pt]
& & B^3\rightarrow&\,(\omega B)^3\\
& & =&\,\,\underset{1}{\underline{\omega^3}}B^3\\
& & =&\,\,1\cdot B^3=B^3
\end{alignat*}
\end{align*}
$$
まとめると、$${A^3, B^3}$$ の行き先は、$${id, \rho_2, \rho_3}$$ の遇置換では式は変化しません。
$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}=id\hspace{5pt}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}=\rho_2\hspace{5pt}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}=\rho_3\hspace{5pt}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&A^3 \longrightarrow A^3\\
&B^3 \longrightarrow B^3\\
&\boldsymbol{変化しない}
\end{align*}
$$
対称性が恒等置換に破壊されたこと
この結果を対称性という観点でとらえると、$${A^3}$$ は遇置換 $${id, \rho_1, \rho_2}$$ のみで変化しない、つまり遇置換シンメトリーをもちます。これは、先ほどやった $${X_3}$$ と同じ対称性です。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&\hspace{5pt}X_3\\
{\small \bm{対称性は同じ}}\updownarrow\hspace{-13pt}&\\
&\hspace{5pt}A^3
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\
\\[-5pt]
\xleftrightarrow[{変化させない置換}]{対応}
\end{align*}
\hspace{5pt}
\begin{align*}
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\updownarrow {\small \bm{対称性は同じ}} (*3)\\
&遇置換 id, \rho_2, \rho_3
\end{align*}
\end{align*}
$$
しかし、$${A^3}$$ の3乗根である $${A}$$ そのものを変化させない置換は恒等置換 $${id}$$ のみであり、遇置換 $${\rho_1, \rho_2}$$ では変化します。つまり、$${A^3}$$ から $${A}$$ にかけて、対称性が遇置換シンメトリーから恒等置換 $${id}$$ まで破壊されたことが分かります。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&\hspace{6pt}A^3\\
{\small \bm{3乗根を取る}}\downarrow\hspace{-13pt}&\\
&\hspace{6pt}A\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[-5pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)} (*4)}\\
&恒等置換 id\\
\end{align*}
\end{align*}
$$
以上の結果と、先に述べた差積 $${X_3}$$ による結果
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&(X_3)^2\\
{\small \bm{平方根を取る}}\downarrow\hspace{-13pt}&\\
&\hspace{5pt}X_3\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[-5pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&3次置換 id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)} (*5)}\\
&遇置換 id, \rho_2, \rho_3\\
\end{align*}
\end{align*}
$$
を、$${(*5) \rightarrow (*3) \rightarrow (*4)}$$ の順につなげると、次のように3次置換から $${id}$$ へといたる対称性の破壊がみられます
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&(X_3)^2\\
{\small \bm{平方根を取る}}\downarrow\hspace{-13pt}&\\
&\hspace{5pt}X_3\\
{\small 対称性は同じ}\updownarrow\hspace{-13pt}&\\
&\hspace{5pt}A^3\\
{\small \bm{3乗根を取る}}\downarrow\hspace{-13pt}&\\
&\hspace{5pt}A
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\
\\[-6pt]
\xleftrightarrow[{変化させない置換}]{対応}\\
\\[-5pt]
\xleftrightarrow[{変化させない置換}]{対応}\\
\\[-5pt]
\xleftrightarrow[{変化させない置換}]{対応}
\end{align*}
\hspace{5pt}
\begin{align*}
&3次置換 id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)}}\\
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\updownarrow {\small 対称性は同じ}\\
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\downarrow {\small \bm{置換の縮小(対称性の破壊)}}\\
&恒等置換 id\\
\end{align*}
\end{align*}
$$
対称性の破壊を体の拡大と関連付ける
次に体の理論に入ります。対称性が $${id}$$ まで破壊されていく過程を、本シリーズ (35) でやった「体の拡大」と関連付けましょう。体という言葉は用いてはいませんが、「累乗根の添加により、構成できる式の範囲(集合)を拡大していく」という意味では、おおむね本シリーズ (12)、(13)、(19) 他と同じ内容です。
差積の添加による体の拡大
3次方程式 $${ax^3+bx^2+cx+d=0}$$ の係数 $${a, b, c, d}$$ と有理数の加減乗除で閉じている体を $${Q_3}$$ とします。
$${Q_3=\hspace{-4pt}}$${係数 $${a, b, c, d}$$ と有理数の加減乗除で閉じている体}
それに、$${1}$$ の3乗根(3乗して $${1}$$ になる数)のうち、複素数である定数 $${\omega}$$ を添加した体を $${Q_3(\omega)}$$ とします。
この $${Q_3(\omega)}$$ を基礎体とします(本シリーズ(35))。拡大する前の最初の体です。係数による体なので、係数体と記しているテキストもあります。
$${\omega}$$ は3乗根を計算するときに必要になります。$${\omega}$$ は複素数であり、有理数の加減乗除だけで作りだすことはできないので、あらかじめ $${Q_3}$$ に添加しておきます。
$${Q_3(\omega)=\hspace{-4pt}}$${係数 $${a, b, c, d}$$、$${\omega}$$ および有理数の加減乗除で閉じている体}
この $${Q_3(\omega)}$$ は3変数のすべての対称式の集合となります。$${Q_2}$$ が2変数のすべての対称式の集合となることと同様の理由です(本シリーズ (19))。
この集合の要素は対称式(または、有理数や $${\omega}$$ の加減乗除で表される定数)で、かつ任意の3変数の対称式を取ってくれば、その対称式は $${Q_3(\omega)}$$ の中に必ず含まれます(注2)。
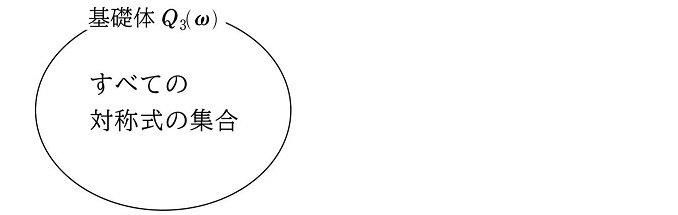
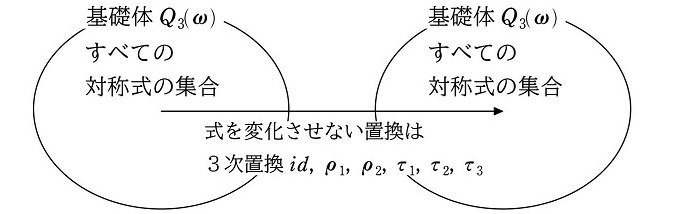
$${Q_3(\omega)}$$ は対称式の集合なので、$${Q_3(\omega)}$$ 内で構成できる(表現できる)すべての式は、3次置換 $${id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3}$$ のすべてにおいて変化しません。
次に、3次方程式 $${ax^3+bx^2+cx+d=0}$$ の解を $${\alpha, \beta, \gamma}$$ とすると、あらためて、その解の差積 $${X_3}$$ は次のようなものでした。
$$
\begin{align*}
X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$
すると、差積の2乗
$${(X_3)^2={\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2}$$
は対称式なので、$${Q_3(\omega)}$$ 内で構成可能、つまり係数 $${a, b, c, d}$$ と $${\omega}$$ と有理数の加減乗除で構成する(表す)ことが可能です。
しかし、その平方根である差積そのもの
$$
\begin{align*}
X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$
は対称式ではないので、$${Q_3(\omega)}$$ 内で構成することはできません。

そこで、この差積 $${X_3}$$ を $${Q_3(\omega)}$$ に添加し、その拡大された体(拡大体)を $${Q_3(\omega, X_3)}$$ とします。
$${Q_3(\omega, X_3)=\hspace{-4pt}}$${係数 $${a, b, c, d}$$、$${X_3}$$、$${\omega}$$、および有理数の加減乗除で閉じている体}
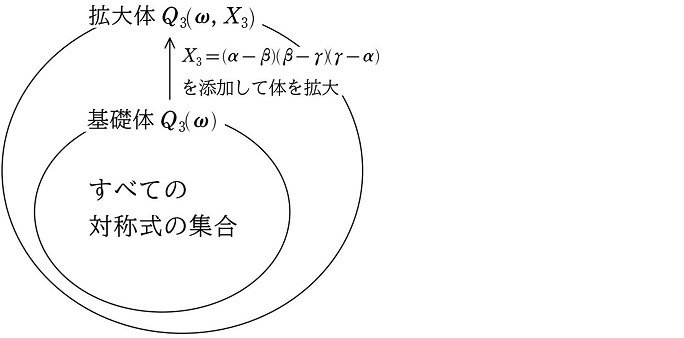
添加した $${X_3}$$ を変化させない置換は遇置換のみでした。よって、拡大体 $${Q_3(\omega, X_3)}$$ 内で構成されるすべての式を変化させない置換も遇置換のみです。
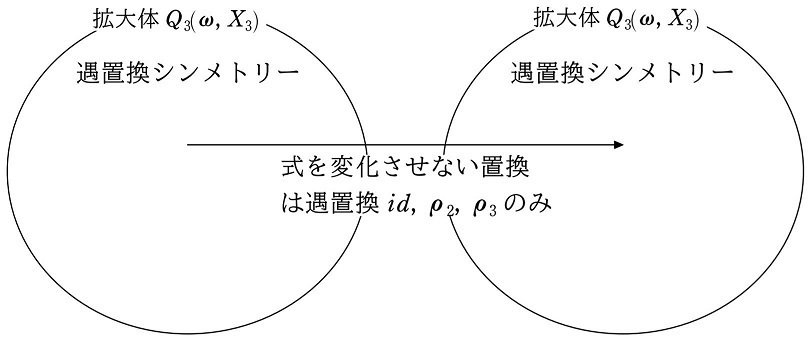
すると、体が拡大するにつれて、その対称性(式を変化させない置換)は対称式(3次置換)から遇置換シンメトリー(遇置換)に破壊されています。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&Q_3(\omega)\\
{\footnotesize X_3 を添加 \atop(体の拡大)}\downarrow\hspace{-20pt}&\\
&Q_3(\omega, X_3)\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[5pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&3次置換 id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\\
&\hspace{10pt}\downarrow {\footnotesize 置換の縮小 \atop(対称性の破壊)}\\
&遇置換 id, \rho_2, \rho_3\\
\end{align*}
\end{align*}
$$
ここまでは、2次方程式と同様の議論です。2次方程式の場合は、差積の添加による体の拡大で、解の公式が実現できました(本シリーズ (36))。
(復習)

差積 $${X_2=\alpha-\beta}$$ の添加による体の拡大により、対称性(式を変化させない置換)は対称式(2次置換)から恒等置換に破壊されます。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&Q_2\\
{\footnotesize X_2 を添加 \atop(体の拡大)}\downarrow\hspace{-8pt}&\\
&Q_2(X_2)\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[5pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&2次置換 id, \rho\\
&\hspace{10pt}\downarrow {\footnotesize 置換の縮小 \atop(対称性の破壊)}\\
&恒等置換 id\\
\end{align*}
\end{align*}
$$
3次方程式の場合はこれで終わりではなく、ラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
の添加によって、さらに体を拡大していきます。
ラグランジュ・リゾルベントの添加による体の拡大
$${Q_3(\omega, X_3)}$$ 内で構成されるすべての式は、遇置換によって変化しません。つまり遇置換シンメトリーをもっているので、同じく遇置換シンメトリーをもつラグランジュ・リゾルベントの3乗 $${A^3}$$ は、$${Q_3(\omega, X_3)}$$ 内で構成できます。
つまり、$${A^3}$$ は係数 $${a, b, c, d}$$、差積 $${X_3}$$、$${\omega}$$、および有理数の加減乗除で構成することができます。
しかし、その3乗恨である $${A}$$ そのものは $${Q_3(\omega, X_3)}$$ 内では構成できません。$${A}$$ を変化させない置換は恒等置換 $${id}$$ のみで、$${\rho_2}$$ や $${\rho_3}$$ では $${A}$$ は変化するからです。

そこで、$${A}$$ を $${Q_3(\omega, X_3)}$$ に添加し、拡大された体(拡大体)を $${Q_3(\omega, X_3, A)}$$ とします。つまり
$${Q_3(\omega, X_3, A)=\hspace{-4pt}}$${係数 $${a, b, c, d}$$、$${\omega}$$、$${X_3}$$、$${A}$$、および有理数の加減乗除で閉じている体}

添加した $${A}$$ を変化させない置換は恒等置換 $${id}$$ のみでした。よって、この拡大体 $${Q_3(\omega, X_3, A)}$$ 内で構成されるすべての式を変化させない置換も恒等置換 $${id}$$ のみです。

すると、体が拡大するにつれて、その対称性は
「3次置換(対称式) $${\rightarrow}$$ 遇置換 $${\rightarrow}$$ 恒等置換」
と、次々と破壊されていくことが分かります。
そして、すべての式を変化させない置換が $${id}$$ のみとなった最後の拡大体 $${Q_3(\omega, X_3, A)}$$ 内で、はれて3次方程式の解の公式が導けるようになります(本シリーズ(13))。

これまでの「累乗根の添加による体の拡大」と「対称性の破壊(式を変化させない置換の縮小)」についてまとめると、次のようになります。
$$
\begin{align*}
\\[-14pt]
\begin{align*}
&Q_3(\omega)\\
{\footnotesize x_3 を添加 \atop(体の拡大)}\downarrow\hspace{-22pt}&\\
&Q_3(\omega, X_3)\\
{\footnotesize A を添加 \atop(体の拡大)}\downarrow\hspace{-22pt}&\\
&Q_3(\omega, X_3, A)\\
\end{align*}
\hspace{5pt}
\begin{align*}
\xleftrightarrow[{変化させない置換}]{対応}\\[1pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[3pt]
\\
\xleftrightarrow[{変化させない置換}]{対応}\\[5pt]
\end{align*}
\hspace{5pt}
\begin{align*}
&3次置換 id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\\
&\hspace{10pt}\downarrow {\footnotesize 置換の縮小 \atop(対称性の破壊)}\\
&遇置換 id, \rho_2, \rho_3\\
&\hspace{10pt}\downarrow {\footnotesize 置換の縮小 \atop(対称性の破壊)}\\
&恒等置換 id
\end{align*}
\end{align*}
$$
次に、ガロアによる群の理論(ガロア対応や可解群)に入ります。これまでの体の拡大を群と結び付けます。
3次対称群のガロア対応
ここではガロアによる群の理論、つまり、3次置換を要素とする3次対称群(本シリーズ (28))
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
のガロア対応をみていきます。
差積と巡回群の同一構造
ここで、これまでの内容をまとめましょう。
すでにやったように
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
に、奇置換 $${\tau_1, \tau_2, \tau_3}$$ のいずれかを作用させると $${-X_3}$$($${-1}$$ 倍)に変化します。すると、もう一度 $${\tau_1, \tau_2, \tau_3}$$ のいずれかを作用させると、さらに $${-1}$$ 倍で元に戻ります。
つまり、差積 $${X_3}$$ と $${-X_3}$$ は、奇置換 $${\tau_1, \tau_2, \tau_3}$$ という演算に関して巡回しています。
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small \tau_1, \tau_2, \tau_3 を作用(-1 倍)}\\
-X_3&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small \tau_1, \tau_2, \tau_3 を作用(-1 倍)}\\
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small \tau_1, \tau_2, \tau_3 を作用(-1 倍)}\\
-X_3&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small \tau_1, \tau_2, \tau_3 を作用(-1 倍)}\\
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small \tau_1, \tau_2, \tau_3 を作用(-1 倍)}\\
&\hspace{6pt}\vdots {\small 巡回的に繰り返される}
\end{align*}
$$
また、$${X_3}$$ と $${-X_3}$$ に、遇置換 $${id, \rho_2, \rho_3}$$ のいずれを作用させても変化しません。
$$
\begin{align*}
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small id, \rho_2, \rho_3 を作用}\\
X_3&=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha) {\small(変化しない)}
\end{align*}
$$
$$
\begin{align*}
-X_2&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\,\downarrow {\small id, \rho_2, \rho_3 を作用}\\
-X_2&=-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha) {\small(変化しない)}
\end{align*}
$$
以上の結果を図示すると、次のように表せます。
(図1)

これと、3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の正規部分群
$${N=\{id, \rho_2, \rho_3\}}$$
による(左)剰余類の集合(剰余群)
$${\{idN, \tau_1N\}}$$
が巡回群になること、詳しくは、$${\tau_1N}$$ を生成元とする巡回群
$${\{idN, \tau_1N\}=\langle\tau_1N\rangle}$$
になることと比較してみましょう(本シリーズ (33))。
なお、$${N}$$ による左剰余類(による類別)と右剰余類(による類別)は、$${N}$$ が正規部分群であるときのみ一致する(正規部分群でないと一致しない)ので、単に剰余類という場合は $${N}$$ が正規部分群である場合を指します(本シリーズ (30))(注3)。
この巡回群 $${\{idN, \tau_1N\}}$$ の要素について、その積の演算表(群表)は次のようになります。
$$
\def\arraystretch{1.5}
\hspace{44pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \utilde{\underline{\tau_1N}}\\ \hline\hline
\underline{idN} & idN & \underline{\tau_1N}\\ \hline
\utilde{\tau_1N} & \tau_1N & \utilde{idN}
\end{array}
$$
これより
$${id N \circ \tau_1N=\tau_1N}$$(下線部)
$${\tau_1N \circ \tau_1N=id N}$$(波線部)
なので、$${id N}$$ に $${\tau_1N}$$ を作用させると $${\tau_1N}$$ に変化し、もう一度 $${\tau_1N}$$ を作用させると元に戻ります。
つまり、巡回群 $${\{idN, \tau_1N\}}$$ の要素は、$${\tau_1N}$$ との積に関して巡回しています。
$$
\begin{align*}
&idN\\
&\,\downarrow {\small \tau_1N を作用}\\
&\tau_1N\\
&\,\downarrow {\small \tau_1N を作用}\\
&idN\\
&\,\downarrow {\small \tau_1N を作用}\\
&\tau_1N\\
&\,\downarrow {\small \tau_1N を作用}\\
&idN\\
&\,\downarrow {\small \tau_1N を作用}\\
&\hspace{6pt}\vdots {\small 巡回的に繰り返される}
\end{align*}
$$
ここで
$${\tau_1N=\tau_2N=\tau_3N}$$
に着目すると、作用させる剰余類は $${\tau_1N}$$ だけでなく、等しい $${\tau_1N, \tau_2N, \tau_3N}$$ のいずれを作用させても巡回します。
$$
\begin{align*}
&idN\\
&\,\downarrow {\small \tau_1N, \tau_2N, \tau_3N を作用}\\
&\tau_1N\\
&\,\downarrow {\small \tau_1N, \tau_2N, \tau_3N を作用}\\
&idN\\
&\,\downarrow {\small \tau_1N, \tau_2N, \tau_3N を作用}\\
&\tau_1N\\
&\,\downarrow {\small \tau_1N, \tau_2N, \tau_3N を作用}\\
&idN\\
&\,\downarrow {\small \tau_1N, \tau_2N, \tau_3N を作用}\\
&\hspace{6pt}\vdots {\small 巡回的に繰り返される}
\end{align*}
$$
また
$$
\def\arraystretch{1.5}
\hspace{44pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & \utilde{\underline{idN}} & \tau_1N\\ \hline\hline
\underline{idN} & \underline{idN} & \tau_1N\\ \hline
\utilde{\tau_1N} & \utilde{\tau_1 N} & idN
\end{array}
$$
より
$${idN \circ idN=idN}$$(下線部)
$${\tau_1N \circ idN=\tau_1N}$$(波線部)
なので、$${idN}$$ と $${\tau_1N}$$ に $${idN}$$ を作用させても変化しません。群のことばでいうと $${idN}$$ は単位元です。
$$
\begin{align*}
&\begin{align*}
&idN\\
&\,\downarrow {\small idN を作用}\\
&idN {\small(変化しない)}
\end{align*}
\hspace{10pt}
&\begin{align*}
&\tau_1N\\
&\,\downarrow {\small idN を作用}\\
&\tau_1N {\small(変化しない)}
\end{align*}
\end{align*}
$$
ここで
$${idN=\rho_2N=\rho_3N}$$
に着目すると、作用させる剰余類は $${idN}$$ だけでなく、等しい $${idN, \rho_2N, \rho_3N}$$ のいずれを作用させても変化しません。
$$
\begin{align*}
&\begin{align*}
&idN\\
&\,\downarrow {\small idN, \rho_2N, \rho_3N を作用}\\
&idN {\small(変化しない)}
\end{align*}
\hspace{10pt}
&\begin{align*}
&\tau_1N\\
&\,\downarrow {\small idN, \rho_2N, \rho_3N を作用}\\
&\tau_1N {\small(変化しない)}
\end{align*}
\end{align*}
$$
以上の結果を図示すると、次のように表せます。
(図2)

(図1)と(図2)を見比べると、2次方程式の解の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
と巡回群
$${\{idN, \tau_1N\}}$$
には、下図のように同じ巡回構造がみてとれます。
<$${\bm{X_3}}$$ について>
(図1)

$${\hspace{52pt}\updownarrow}$$ 同じ巡回構造
<$${\bm{\{idN, \tau_1N\}}}$$ について>
(図2)

さらに、等しい剰余類
$${idN=\rho_2N=\rho_3N}$$
と
$${\tau_1N=\tau_2N=\tau_3N}$$
に着目すると、3つある遇置換 $${id, \rho_2, \rho_3}$$ の役割を、$${id}$$ を代表元とする剰余類 $${idN}$$ に(代表として)担わせることができ、3つある奇置換 $${\tau_1, \tau_2, \tau_3}$$ の役割を、$${\tau_1}$$ を代表元とする剰余類 $${\tau_1N}$$ に(代表として)担わせることができます。
<$${\bm{X_3}}$$ について>

$${\hspace{60pt}\updownarrow}$$ 同じ巡回構造
<$${\bm{\{idN, \tau_1N\}}}$$ について>

なお、代表元は等しい剰余類のうちのどれを選んでもかまいません。
つまり、$${idN}$$ の代わりにそれと等しい $${\rho_2N}$$ を選んでも、$${\tau_2N}$$ の代わりにそれと等しい $${\tau_3N}$$ を選んでも同様の議論になります。
これはいわば、等しい剰余類の”団体行動”のようなイメージです。
等しい剰余類を”団体”とすることによって、それが対称性をいざなう遇置換(不変をいざなう”団体”)と奇置換(巡回をいざなう”団体”)に対応していることが、正規部分群による剰余類の威力であり、ガロアの発見の偉大な所です。

数学は、同じ構造のものを同一視して考えることがよくあります。
つまり、「差積 $${X_3}$$ が奇置換の作用で巡回すること」と「剰余群 $${\{idN, \tau_1N\}}$$ の要素が($${id}$$ を代表元とする)剰余類 $${idN}$$ の積で巡回すること(巡回群になること)」を、同一の構造とみることができます。
また、「差積 $${X_3}$$ と $${-X_3}$$ が遇置換の作用で変化しないこと」と「剰余群 $${\{idN, \tau_1N\}}$$ の要素が($${\tau_1}$$ を代表元とする)剰余類 $${\tau_1N}$$ の積で変化しないこと」も、同一の構造とみることができます。
同一の構造とみることによって、「差積 $${X_3}$$ の添加」と「剰余群 $${\{idN, \tau_1N\}}$$ が巡回群になること」を結びつけることができます。後に重要になるので、このことを $${(*)}$$ とします。
「差積 $${X_3}$$ の添加」$${\leftrightarrow}$$「剰余群 $${\{idN, \tau_1N\}}$$ が巡回群になること」 $${\cdots (*)}$$
ここまで、差積と巡回群の同一構造をみてきました。
次に、ラグランジュ・リゾルベントと巡回群の同一構造をみていきます。
ラグランジュ・リゾルベントと巡回群の同一構造
次に、ラグランジュ・リゾルベント $${A}$$ に遇置換 $${id, \rho_2, \rho_3}$$ を作用させた変化をみていきます。
すでにやったように
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
に $${\rho_2}$$ を作用させると $${\omega A}$$($${\omega}$$ 倍)に変化します。
(再掲)
$${➁}$$ $${\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}=\rho_2}$$ を作用させる
$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換なので
$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow {\small 置き換え}\\
&\gamma+\omega\alpha+\omega^2\beta\\
=\,&\underset{1}{\underline{\omega^3}}\,\gamma+\omega\alpha+\omega^2\beta\\
=\,&\omega(\omega^2\gamma+\alpha+\omega\beta)\\
=\,&\omega(\alpha+\omega\beta+\omega^2\gamma)=\omega A \Rightarrow {\small \omega 倍に変化}
\end{align*}
$$
すると、もう一度 $${\rho_2}$$ を作用させると $${\omega^2 A}$$ に変化し、さらに $${\rho_2}$$ を作用させると $${A}$$ と元に戻ります($${\omega^3=1}$$ より)。
つまり、ラグランジュ・リゾルベント $${A}$$、$${\omega A}$$、$${\omega^2A}$$ は、$${\rho_2}$$ という演算に関して巡回しています。なお、$${\omega}$$ は3乗して $${1}$$ になる複素数なので $${\omega^3=1}$$ です。
$$
\begin{align*}
A&=\alpha+\omega\beta+\omega^2\gamma\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
\omega A&=\omega(\alpha+\omega\beta+\omega^2\gamma)\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
\omega^2A&=\omega^2(\alpha+\omega\beta+\omega^2\gamma)\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
A&=\alpha+\omega\beta+\omega^2\gamma\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
\omega A&=\omega(\alpha+\omega\beta+\omega^2\gamma)\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
\omega^2A&=\omega^2(\alpha+\omega\beta+\omega^2\gamma)\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
A&=\alpha+\omega\beta+\omega^2\gamma\\
&\,\downarrow {\small \rho_2 を作用(\omega 倍)}\\
&\hspace{6pt}\vdots {\small 巡回的に繰り返される}
\end{align*}
$$
また、$${A}$$、$${\omega A}$$、$${\omega^2A}$$ のいずれに恒等置換 $${id}$$ を作用させても変化しません。
$$
\begin{align*}
A&=\alpha+\omega\beta+\omega^2\gamma\\
&\,\downarrow {\small id を作用}\\
A&=\alpha+\omega\beta+\omega^2\gamma {\small(変化しない)}\\[18pt]
\omega A&=\omega(\alpha+\omega\beta+\omega^2\gamma)\\
&\,\downarrow {\small id を作用}\\
\omega A&=\omega(\alpha+\omega\beta+\omega^2\gamma) {\small(変化しない)}\\[18pt]
\omega^2A&=\omega^2(\alpha+\omega\beta+\omega^2\gamma)\\
&\,\downarrow {\small id を作用}\\
\omega^2A&=\omega^2(\alpha+\omega\beta+\omega^2\gamma) {\small(変化しない)}
\end{align*}
$$
以上の結果を図示すると、次のように表せます。
(図3)

これと、$${S_3}$$ の正規部分群
$${N=\{id, \rho_2, \rho_3\}}$$
の、さらにその正規部分群
$${I=\{id\}}$$
による剰余類の集合(剰余群)
$${\{idI, \rho_2I, \rho_3I\}}$$
が巡回群になること、詳しくは、$${\rho_2I}$$ を生成元とする巡回群
$${\{idI, \rho_2I, \rho_3I\}=\langle\rho_2I\rangle}$$
になることと比較してみましょう(本シリーズ (33))。
この巡回群 $${\{idI, \rho_2I, \rho_3I\}}$$ の要素について、その積の演算表(群表)は次のようなものでした。
$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-15pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \underlinesegment{\utilde{\underline{\rho_2I}}} & \rho_3I\\ \hline\hline
\underline{idI} & idI & \underline{\rho_2I} & \rho_3I\\ \hline
\utilde{\rho_2I} & \rho_2I & \utilde{\rho_3I} & idI\\ \hline
\underlinesegment{\rho_3I} & \rho_3I & \underlinesegment{idI} & \rho_2I
\end{array}
$$
これより
$${id I \circ \rho_2I=\rho_2I}$$(下線部)
$${\rho_2I \circ \rho_2I=\rho_3I}$$(波線部)
$${\rho_3I \circ \rho_2I=id I}$$($${\underlinesegment{\hspace{5pt}}}$$ 線部)
なので、$${id I}$$ に $${\rho_2I}$$ を作用させると $${\rho_2I}$$ に変化し、もう一度 $${\rho_2I}$$ を作用させると $${\rho_3I}$$ に変化し、さらにもう一度 $${\rho_2I}$$ を作用させると元に戻ります。
つまり、巡回群 $${\{idI, \rho_2I, \rho_3I\}}$$ の要素は、$${\rho_2I}$$ との積に関して巡回しています。
$$
\begin{align*}
&idI\\
&\,\downarrow {\small \rho_2I を作用}\\
&\rho_2I\\
&\,\downarrow {\small \rho_2I を作用}\\
&\rho_3I\\
&\,\downarrow {\small \rho_2I を作用}\\
&idI\\
&\,\downarrow {\small \rho_2I を作用}\\
&\rho_2I\\
&\,\downarrow {\small \rho_2I を作用}\\
&\rho_3I\\
&\,\downarrow {\small \rho_2I を作用}\\
&idI\\
&\,\downarrow {\small \rho_2I を作用}\\
&\hspace{6pt}\vdots {\small 巡回的に繰り返される}
\end{align*}
$$
また
$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-15pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \underlinesegment{\utilde{\underline{idI}}} & \rho_2I & \rho_3I\\ \hline\hline
\underline{idI} & \underline{idI} & \rho_2I & \rho_3I\\ \hline
\utilde{\rho_2I} & \utilde{\rho_2I} & \rho_3I & idI\\ \hline
\underlinesegment{\rho_3I} & \underlinesegment{\rho_3I} & idI & \rho_2I
\end{array}
$$
より
$${idI \circ idI=idI}$$(下線部)
$${\rho_2I \circ idI=\rho_2I}$$(波線部)
$${\rho_3I \circ idI=\rho_3I}$$($${\underlinesegment{\hspace{5pt}}}$$ 線部)
なので、$${idI, \rho_2I, \rho_3I}$$ に $${idI}$$ を作用させても変化しません。群のことばでいうと $${idI}$$ は単位元です。
$$
\begin{align*}
&\begin{align*}
&idI\\
&\,\downarrow {\small idI を作用}\\
&idI {\small(変化しない)}
\end{align*}
\hspace{-4pt}
&\begin{align*}
&\rho_2I\\
&\,\downarrow {\small idI を作用}\\
&\rho_2I {\small(変化しない)}
\end{align*}
\hspace{3pt}
&\begin{align*}
&\rho_3I\\
&\,\downarrow {\small idI を作用}\\
&\rho_3I {\small(変化しない)}
\end{align*}
\end{align*}
$$
以上の結果を図示すると、次のように表せます。
(図4)

すると、ラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
と巡回群
$${\{idI, \rho_1I, \rho_3I\}}$$
には、下図のように同じ巡回構造がみてとれます。
<$${\bm{A}}$$ について>
(図3)

$${\hspace{59pt}\updownarrow}$$ 同じ巡回構造
<$${\bm{\{idI, \rho_2I, \rho_3I\}}}$$ について>
(図4)

ここでも、同じ構造のものを同一視します。
つまり、「差積 $${A}$$ が置換 $${\rho_2}$$ に関して巡回すること」と「剰余群 $${\{idI, \rho_2I, \rho_3I\}}$$ の要素が $${\rho_2I}$$ に関して巡回すること(巡回群になること)」を同一の構造とみることができます。同一の構造とみることによって、「差積 $${A}$$ の添加」と「剰余群 $${\{idI, \rho_2I, \rho_3I\}}$$ が巡回群になること」を結びつけることができます。後に重要になるので、このことを $${(**)}$$ とします。
「差積 $${A}$$ の添加」$${\leftrightarrow}$$「剰余群 $${\{idI, \rho_2I, \rho_3I\}}$$ が巡回群になること」 $${\cdots (**)}$$
次に、「体の拡大」と「群の縮小」の対応関係をみていきます。
「体の拡大」と「群の縮小」の対応
体 $${Q_3(\omega)}$$ は3変数のすべての対称式の集合でした(注2)。よって、3次置換を作用させても $${Q_3(\omega)}$$ 内のすべての式を変化させません。
3次置換をすべて集めた集合は、3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
です(本シリーズ (28))。これにより、体 $${Q_3(\omega)}$$ と群 $${S_3}$$ の対応関係が生まれます。
$$
\begin{align*}
体 Q_3(\omega) \xleftrightarrow[対応]{} 群 S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}
\end{align*}
$$
さらに、$${Q_3(\omega)}$$ に差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を添加した拡大体を $${Q_3(\omega, X_3)}$$ とすると、添加された $${X_3}$$ を変化させない置換は遇置換 $${id, \rho_2, \rho_3}$$ のみです(奇置換では変化する)。よって、 $${Q_3(\omega, X_3)}$$ 内のすべての式を変化させない置換も偶置換 $${id, \rho_2, \rho_3}$$ のみとなります。

偶置換のみを要素とする集合は、3次対称群 $${S_3}$$ の正規部分群
$${N=\{id, \rho_2, \rho_3\}}$$
です。これで、体 $${Q_3(\omega, X_3)}$$ と正規部分群 $${N}$$ の対応関係が生まれます。
$$
\begin{align*}
体 Q_3(\omega, X_3) \xleftrightarrow[対応]{} 正規部分群 N=\{id, \rho_2, \rho_3\}
\end{align*}
$$
さらに、$${Q_3(\omega, X_3)}$$ にラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
を添加した拡大体を $${Q_3(\omega, X_3, A)}$$ とすると、添加された $${A}$$ を変化させない置換は恒等置換 $${id}$$ のみです($${\rho_2, \rho_3}$$ では変化する)。よって、$${Q_3(\omega, X_3, A)}$$ 内のすべての式を変化させない置換も恒等置換 $${id}$$ のみとなります。

恒等置換のみを要素とする集合は、$${N=\{id, \rho_2, \rho_3\}}$$ の正規部分群
$${I=\{id\}}$$
です。これで、体 $${Q_3(\omega, X_3, A)}$$ と正規部分群 $${I=\{id\}}$$ の対応関係が生まれます。
$$
\begin{align*}
体 Q_3(\omega, X_3, A) \xleftrightarrow[対応]{} 正規部分群 I=\{id\}
\end{align*}
$$
これにより、「体の拡大」と「群の縮小」という、次のような対応関係が得られます。
$$
\begin{align*}
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\[-3pt]
&\hspace{17pt}\Updownarrow\hspace{7pt}{\footnotesize 対応}\hspace{7pt}\Updownarrow\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}
\end{align*}
$$
体が拡大するのに対応して群は縮小します。「拡大」と「縮小」で逆の関係になります。
しかし、これだけだとただ対応させているだけなので、この対応を群構造の面から補強します。それが、先ほどやった $${(*)}$$ と $${(**)}$$ の対応関係です。
(再掲)
「差積 $${X_3}$$ の添加」$${\leftrightarrow}$$「剰余群 $${\{idN, \tau_1N\}}$$ が巡回群になること」 $${\cdots (*)}$$
「ラグランジュ・リゾルベント $${A}$$ の添加」$${\leftrightarrow}$$「剰余群 $${\{idI, \rho_2I, \rho_3I\}}$$ が巡回群になること」
$${\cdots (**)}$$
「添加」と「巡回群」の対応
この $${(*)}$$ と $${(**)}$$ によって、単に「体の拡大」と「群の縮小」の対応ではなく、拡大と縮小の部分(接続部分)に「差積、およびラグランジュ・リゾルベントの添加」と「剰余群が巡回群となること」という構造的な対応が導かれます。この対応も含めた「体の拡大」と「群の縮小」の対応をガロア対応といいます(下図)。
$$
\begin{align*}
&\hspace{-2pt}{\footnotesize X_3 を添加 (*)}\hspace{2pt}{\footnotesize A を添加 (**)}\\[-4pt]
&\hspace{17pt}\downarrow\hspace{37pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\[-3pt]
&\hspace{17pt}\Updownarrow\hspace{7pt}{\footnotesize 対応}\hspace{7pt}\Updownarrow\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN, \tau_1N\} \atop が巡回群 (*)}\hspace{2pt}{\footnotesize \{idI, \rho_2I, \rho_3I\} \atop が巡回群 (**)}
\end{align*}
$$
$${Q_3(\omega)}$$ を基礎体とし、3次方程式の3つの解の差積
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
の添加は平方恨の添加に相当します(本シリーズ (12))。またラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
の添加は3乗根の添加に相当します(本シリーズ (13) )。剰余類の集合 $${\{id N, \tau_1N\}}$$ と $${\{id I, \rho_2I, \rho_3I\}}$$ が、ともにただの群(剰余群)ではなく巡回群になることが重要です。ともに巡回群でなければガロア対応になりません。
そして、3乗根まで添加された拡大体 $${Q_3(\omega, X_3, A)}$$ 内で、3次方程式の解の公式は構成可能となります。

3次対称群が可解群となること
すると、先ほどの3次対称群 $${S_3}$$ のガロア対応から、次のような「正規部分群の縮小の列」が存在することになります。上記のガロア対応の<群の縮小>のみを抜き出しています。
$$
\begin{align*}
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I} \cdots (*4)\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN, \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI, \rho_2I, \rho_3I\} \atop が巡回群}
\end{align*}
$$
このような、正規部分群による剰余類の集合(剰余群)が巡回群となるルールを保ちながら
「 $${I=\{id\}}$$ へといたる正規部分群の縮小の列」
をもつ群のことを可解群といいます。解の公式が存在するかどうかは可解群であるかどうかによります。すると $${S_3}$$ は可解群です。つまり
$${S_3}$$ は可解群となるので、3次方程式に解の公式が存在する。
となります。これが、3次方程式に解の公式が存在することの証明です。可解群かどうかという群の構造を考えれば、解の公式が存在するかどうかを判定できるのです。
4次方程式について
4次方程式については本シリーズでは解説していませんが、4次方程式の4つの解の置換を要素とする4次対称群 $${S_4}$$ は可解群であるので、それをもって4次方程式に解の公式が存在することが証明されます。
$${S_4}$$ は可解群となるので、4次方程式に解の公式が存在する。
証明の方は専門書にゆずりたいと思います。3次方程式のときと同様の議論を辿っていきます。
5次方程式について
いよいよ次の章で、5次以上の方程式に解の公式が存在しないことの証明を行います。証明すべき命題は「5次対称群 $${S_5}$$ は可解群ではない」ことです。次の章でこの命題を証明します。
(続く)
(コメント)
もう一度か二度推敲をしたかったですが、時間がいくらあっても終わらないので次の章に進みます。次は作成の一番難しい章になりそうです。
(注1)一般の3次方程式を考えること
$${ax^3+bx^2+cx+d=0}$$ の解を $${\alpha_1, \beta_1, \gamma_1}$$、チルンハウス変換された $${y^3+py+q=0}$$ の解を $${\alpha_2, \beta_2, \gamma_2}$$ と置くと
$$
\begin{align*}
ax^3+bx^2+cx+d&=0\\
&\hspace{-20pt}\downarrow \Leftarrow {\footnotesize x=y-\dfrac{b}{3a} と置く \atop(チルンハウス変換)}\\
y^3+py+q&=0
\end{align*}
$$
より、$${\alpha_1, \beta_1, \gamma_1}$$ と $${\alpha_2, \beta_2, \gamma_2}$$ の間には
$${x=y-\dfrac{b}{3a}}$$
の関係、つまり
$$
\begin{align*}
\alpha_1=\alpha_2-\dfrac{b}{3a}\\[8pt]
\beta_1=\beta_2-\dfrac{b}{3a}\\[8pt]
\gamma_1=\gamma_2-\dfrac{b}{3a}
\end{align*}
$$
という関係が成り立ちます。
するとこの対応により、解 $${\alpha_1, \beta_1, \gamma_1}$$ が存在すれば解 $${\alpha_2, \beta_2, \gamma_2}$$ も存在し、またその逆もいえるので、一般の3次方程式 $${ax^3+bx^2+cx+d=0}$$ に解の公式が存在することと、チルンハウス変換された $${y^3+py+q=0}$$ に解の公式が存在することは同値になります。
つまり、
「$${ax^3+bx^2+cx+d=0}$$ に解の公式が存在すれば、$${y^3+py+q=0}$$ に解の公式が存在する」
またその逆
「$${y^3+py+q=0}$$ に解の公式が存在すれば、$${ax^3+bx^2+cx+d=0}$$ に解の公式が存在する」
の両方が成り立ちます。
よって、 チルンハウス変換は解の公式を導き出すには有効ですが、解の置換による群構造を用いて解の公式が存在するかどうかを議論する上では本質的ではない(必ずしも必要ではない)ので、この章では、$${ax^3+bx^2+cx+d=0}$$ の解を $${\alpha, \beta, \gamma}$$ とし、その解の置換による群構造を考えることによって、3次方程式に解の公式が存在することを証明しています。
(注2)Q(ω)とすべての対称式の集合が一致すること
$${Q_3(\omega)=\hspace{-4pt}}$${係数 $${a, b, c, d}$$ と $${\omega}$$ と有理数の加減乗除で閉じている体}
について、この体 $${Q_3}$$ が、3変数のすべての対称式の集合と一致すること(これを「定理A」とします)を証明します。つまり
$$
\begin{align*}
体 Q_3= すべての対称式の集合(定理A)
\end{align*}
$$

厳密な証明ではなく、具体例をつかった形で簡単に述べます。イメージがつかめればよいと思います。なお、$${2}$$ や $${-\dfrac{3}{4}\omega}$$ のような有理数や $${\omega}$$ による定数は、どちらの集合にもすべて含まれているとします。
この「定理A」の証明(集合が一致することの証明)には、以下の (case1) と (case2) の2つを証明する必要があります。
(case1)
3次方程式の係数 $${a, b, c, d}$$、有理数、および $${\omega}$$ の加減乗除で表された式ならば、その式は3変数の対称式である。平たくいえば
「係数の式 $${\xrightarrow[ならば]{}}$$ 対称式」
および、その逆
(case2)
(有理数および $${\omega}$$ を係数として用いた)3変数の対称式ならば、それは3次方程式の係数 $${a, b, c, d}$$、有理数、および $${\omega}$$ の加減乗除で表せる。平たくいえば
「対称式 $${\xrightarrow[ならば]{}}$$ 係数の式」
(証明のイメージ)

(case1) の簡単な証明
まずは、3変数の<解と係数の関係>を復習します。
<解と係数の関係>
3次方程式 $${ax^3+bx^2+cx+d=0}$$ の3つの解を $${\alpha, \beta, \gamma}$$ とすると
$$
\begin{align*}
&\alpha+\beta+\gamma=-\dfrac{b}{a}\\
&\alpha\beta\gamma=\dfrac{c}{a}\\
&\alpha\beta+\beta\gamma+\gamma\alpha=-\dfrac{d}{a}
\end{align*}
$$
***
文字を入れ替えても変化しない式を対称式といいますが、そのうち
$$
\begin{align*}
&\alpha+\beta+\gamma\\
&\alpha\beta\gamma\\
&\alpha\beta+\beta\gamma+\gamma\alpha
\end{align*}
$$
を3変数の基本対称式といいます。すると、この<解と係数の関係>から、3変数の基本対称式は、すべて3次方程式の係数 $${a, b, c, d}$$ で表せることが分かります。
$$
\begin{align*}
&\underset{基本対称式}{\underline{\alpha+\beta+\gamma}}=-\dfrac{b}{a}\\
&\underset{基本対称式}{\underline{\alpha\beta\gamma}}=\dfrac{c}{a}\\
&\underset{基本対称式}{\underline{\alpha\beta+\beta\gamma+\gamma\alpha}}=-\dfrac{d}{a}
\end{align*}
$$
ここで、両辺を入れ替えて
$$
\begin{align*}
-\dfrac{b}{a}&=\alpha+\beta+\gamma\\[8pt]
\dfrac{c}{a}&=\alpha\beta\gamma\\[8pt]
-\dfrac{d}{a}&=\alpha\beta+\beta\gamma+\gamma\alpha
\end{align*}
$$
第1式と第3式の両辺にマイナスをかけて
$$
\begin{align*}
\dfrac{b}{a}&=-(\alpha+\beta+\gamma)\\[8pt]
\dfrac{c}{a}&=\alpha\beta\gamma\\[8pt]
\dfrac{d}{a}&=-(\alpha\beta+\beta\gamma+\gamma\alpha)
\end{align*}
$$
さらに、両辺に $${a}$$ をかけて
$$
\begin{alignat*}{2}
b&=-(\alpha+\beta+\gamma)a & &\cdots ➀\\
c&=\alpha\beta\gamma a & &\cdots ➁\\
d&=-(\alpha\beta+\beta\gamma+\gamma\alpha)a & &\cdots ➂
\end{alignat*}
$$
すると、例えば $${a+b+c+d}$$ は対称式になるでしょうか?
これには、先ほどの $${➀, ➁, ➂}$$ を代入すれば
$$
\begin{align*}
&a+b+c+d\\
=&a-(\alpha+\beta+\gamma)a+\alpha\beta\gamma a-(\alpha\beta+\beta\gamma+\gamma\alpha)a\\
=&\{1-(\alpha+\beta+\gamma)+\alpha\beta-(\alpha\beta+\beta\gamma+\gamma\alpha)\}a
\end{align*}
$$
と、基本対称式
$$
\begin{align*}
&\alpha+\beta+\gamma\\
&\alpha\beta\gamma\\
&\alpha\beta+\beta\gamma+\gamma\alpha
\end{align*}
$$
と有理数 $${a}$$ の加減乗除で表されるので、$${a+b+c}$$ は対称式になります。基本対称式と有理数の加減乗除で表された式は、$${\alpha, \beta, \gamma}$$ をどのように入れ替えても変化しないので対称式です。定数 $${a}$$ は $${\alpha, \beta, \gamma}$$ を入れ替えても変化しないので、残っていても問題ありません。
一般に、基本対称式と有理数と $${\omega}$$ の加減乗除で表された式はすべて対称式となるので、集合 $${Q_3(\omega)}$$ 内の式はすべて対称式となります。
(case2) の簡単な証明
これには次の定理
<対称式の基本定理>
すべての対称式は、基本対称式の加減乗除で表すことができる
***
を用います。<対称式の基本定理>より、対称式はかならず基本対称式の加減乗除で表すことができます。すると、その基本対称式に<解と係数の関係>
$$
\begin{align*}
&\underset{基本対称式}{\underline{\alpha+\beta+\gamma}}=-\dfrac{b}{a}\\
&\underset{基本対称式}{\underline{\alpha\beta\gamma}}=\dfrac{c}{a}\\
&\underset{基本対称式}{\underline{\alpha\beta+\beta\gamma+\gamma\alpha}}=-\dfrac{d}{a}
\end{align*}
$$
を代入すれば、必ず3次方程式の係数 $${a, b, c, d}$$ で表わすことができきます。
例えば、対称式 $${\alpha^2+\beta^2+\gamma^2}$$ について考えると、高校1年でならう次の展開公式
$$
\begin{align*}
(\alpha+\beta+\gamma)^2=\alpha^2+\beta^2+\gamma^2+2\alpha\beta+2\beta\gamma+2\gamma\alpha
\end{align*}
$$
より、左右入れ替えて
$$
\begin{align*}
\alpha^2+\beta^2+\gamma^2+2\alpha\beta+2\beta\gamma+2\gamma\alpha=(\alpha+\beta+\gamma)^2
\end{align*}
$$
$${2\alpha\beta+2\beta\gamma+2\gamma\alpha}$$ を移項して
$$
\begin{align*}
\alpha^2+\beta^2+\gamma^2&=(\alpha+\beta+\gamma)^2-2\alpha\beta-2\beta\gamma-2\gamma\alpha\\
&=(\underset{基本対称式}{\underline{\alpha+\beta+\gamma}})^2-2(\underset{基本対称式}{\underline{\alpha\beta+\beta\gamma+\gamma\alpha}})
\end{align*}
$$
と基本対称式の加減乗除で表されるので、これに先ほど導いた<解と係数の関係>
$$
\begin{align*}
&\underset{基本対称式}{\underline{\alpha+\beta+\gamma}}=-\dfrac{b}{a}\\
&\underset{基本対称式}{\underline{\alpha\beta\gamma}}=\dfrac{c}{a}\\
&\underset{基本対称式}{\underline{\alpha\beta+\beta\gamma+\gamma\alpha}}=-\dfrac{d}{a}
\end{align*}
$$
の第1式と第3式を代入すれば
$$
\begin{align*}
\alpha^2+\beta^2+\gamma^2&=(\alpha+\beta+\gamma)^2-2\alpha\beta-2\beta\gamma-2\gamma\alpha\\
&=(\underset{基本対称式}{\underline{\alpha+\beta+\gamma}})^2-2(\underset{基本対称式}{\underline{\alpha\beta+\beta\gamma+\gamma\alpha}})\\
&={\left(-\dfrac{b}{a}\right)}^2-2\left(-\dfrac{d}{a}\right)\\
&={\left(\dfrac{b}{a}\right)}^2+2\cdot\dfrac{d}{a}
\end{align*}
$$
となり、これで3次方程式の係数 $${a, b, c, d}$$ と有理数(ここでは $${2}$$)で表すことができました。
一般に、すべての対称式は基本対称式の加減乗除で表され(対称式の基本定理)、さらにそれは3次方程式の係数 $${a, b, c, d}$$ の加減乗除で表すことができるので(解と係数の関係)、すべての対称式は集合 $${Q_3(\omega)}$$ に含まれることが分かります。
以上により、(case1) と (case2) の両方が示されたので、これによって「定理A」が証明されました。
(注3)剰余類について若干の注意
確認のため、ここで正規部分群の定義を復習します(本シリーズ (30))。
<正規部分群の定義>(復習)
$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について
$$
\begin{align*}
gN=Ng
\end{align*}
$$
を満たすとき、$${N}$$ を $${G}$$ の『正規部分群』という。
***
この定義により、正規部分群による左剰余類と右剰余類は等しくなります。
$$
\begin{gather*}
\underset{左剰余類}{gN}\hspace{-5pt}=\hspace{-5pt}\underset{右剰余類}{Ng}\\[-3pt]
\hspace{1pt}\uparrow\\[-5pt]
\hspace{1pt}{\footnotesize 等しい}
\end{gather*}
$$
$${N=\{id, \rho_2, \rho_3\}}$$ は3次対称群 $${S_3}$$ の正規部分群なので、$${N}$$ による左剰余類と右剰余類は等しくなります。つまり、左剰余類と右剰余類、どちらで考えても同じ議論となります。
本シリーズでは左剰余類の方を採用しています(もちろん右剰余類を採用しても問題ありません。左なら左、右なら右と最後まで一貫させることが重要です)。
なお、$${N}$$ による左剰余類(による類別)と右剰余類(による類別)は、$${N}$$ が正規部分群であるときのみ一致する(正規部分群でないと一致しない)ので、単に剰余類という場合は $${N}$$ が正規部分群である場合を指します(本シリーズ (30))
また、$${N=\{id, \rho_2, \rho_3\}}$$ による左剰余類は全部で
$${idN, \rho_2N, \rho_3N, \tau_1N, \tau_2N, \tau_3N}$$
の6通りありますが
$${idN=\rho_2N=\rho_3N(=\{id, \rho_2, \rho_3\})}$$
$${\tau_1N=\tau_2N=\tau_3N(=\{\tau_1, \tau_2, \tau_3\})}$$
と、2つのグループに分かれます(本シリーズ (31))。
そこで、それぞれの代表元を $${id}$$ と $${\tau_1}$$ として選んだ集合が、本文中の
$${\{idN, \tau_1N\} \cdots (*1)}$$
という集合です。つまり、下線部
$${\underline{id}N=\rho_2N=\rho_3N}$$
$${\underline{\tau_1}N=\tau_2N=\tau_3N}$$
を代表元として選んでいます。例えば代表元を別のものして
$${\{idN, \tau_2N\} \cdots (*2)}$$
や
$${\{\rho_2N, \tau_3N\} \cdots (*3)}$$
を選んでも、代表元が違うだけで $${(*1), (*2), (*3)}$$ はすべて同じ集合になるので、同じ議論となることを注意しておきます。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベントの連立」による「3次方程式の解の公式」の導出
(8)「遇置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む(対称性の破壊)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(対称性の破壊)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から遇置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての遇置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
(19)もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
(20)もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
(21)もっと分かりやすくシリーズ➃ 何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
(22)もっと分かりやすくシリーズ➄「解の和と差の連立」による2次方程式の解の公式の導出について。
(23)もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
(24)もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
(25)もっと分かりやすくシリーズ➇ 3次方程式の解の公式の導出方法「カルダノの方法」を復習
(26)もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
(27)もっと分かりやすくシリーズ⑩ そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
(28)中学でも分かるガロアの証明① ガロアの発見した「群」について簡単に解説
(29)中学でも分かるガロアの証明➁ ガロアの発見した「部分群」について簡単に解説
(30)中学でも分かるガロアの証明③ ガロアの発見した「正規部分群」について
(31)中学でも分かるガロアの証明➃ 正規部分群による剰余類の集合が群(剰余群)になること
(32)中学でも分かるガロアの証明⑤ 単位元のみの正規部分群 $${\{𝑖𝑑\}}$$ による剰余類の集合が群(剰余群)になること
(33)中学でも分かるガロアの証明⑥ 「巡回群」について、および剰余群が巡回群になること
(34)中学でも分かるガロアの証明⑦ 2次対称群で、正規部分群による剰余群が巡回群になることの復習
(35)中学でも分かるガロアの証明⑧ 「体」について解説
(36)中学でも分かるガロアの証明➈ 2次方程式に解の公式が存在することを、2次対称群が「可解群」になることによって証明する
