
【高校数学】三角形の五心を復習する
皆さんこんにちは!
日常の中で様々なことに疑問を持ち、学んでいっているのですが、せっかくなのでそれを発信していき、共有していこうと思っている、そんな企画でございます。
今回は数学Aとかで出てくる三角形の五心について復習していきます!
五大老
突然ですがみなさん「五大老」という言葉をご存じですか?

安土桃山時代、豊臣秀吉に仕えていた部下のトップ5のことを「五大老」というそうです。
日本ではよく、トップ○に対して異名がついていますよね。
トップ3のことを「御三家」といい、トップ4のことを「四天王」と言ったりします。要はそれのトップ5版ですね。
「5本の指に入る」とかも言いますし、やはり目立つ5つのものって独特のオーラを放っていますよね。
ちなみにその五大老というのは、

徳川家康

毛利輝元

上杉景勝

前田利家

宇喜多秀家
の5人だそうです。
なんだか秀吉の部下に家康がいるっていうのが胸熱ですよね。
さてさて、そんな五大老的な存在が三角形にも存在しています。
三角形であるならば自然と成立する5つの"中心"。その名も「三角形の五心」。
それぞれがどのような性質であったかを再確認していきましょう。
ちなみに、学生時代にバンドを組んでいた僕としては、5という数字を聞くとバンドメンバーっぽさをイメージしてしまうのですよね。
なので、今回は三角形の五心たちがバンドメンバーだったらどのパートを担当しているのかを考えながら紹介していきたいと思います。
※数学的な議論をする際に、厳密な証明等が必要となりますが、今回は全て省いていきます。数学が苦手な方を配慮しているためではなく、単純に面倒くさいからです。
なお、五心の性質の証明に関しては古賀さんの動画が詳しいです。
それと、それぞれベクトル的性質と初等幾何的性質を持っていますが、今回は初等幾何的性質のみ扱います。
ベクトル的性質は非常に美しい式で表されるのですが、こちらも理由は純粋に面倒くさいからです。
ベクトルをパソコン上の文章で表現するって非常にやりづらいのです。
三角形の五心とは
三角形の五心とは、ある条件の下で三角形上に直線を引いていくと、3本の直線がある1点で交わるよ~という性質です。
その条件が5種類あり、それぞれの条件で直線が交わる点を合わせて「五心」というわけですね。
んで、あまり深く考える人はいないかと思いますが、「線を3本引くと、1点で交わる。」って実はめちゃくちゃレアケースなんです。
かっこいい言い方をすると「3本の直線を引いたとき、それがある1点で交わることは全く自明ではない。」のです!
3本の線が1点で交わるキセキ
では、皆さん紙とペンをご用意ください。
そして、適当に2本の線を引いてみてください。
この時、2本の線が完璧に平行でなければ延長線上のどこかで交わることになります。(ユークリッド平面上とする)

2本の直線はてきとーに引いてもほぼ確実に交わる
次に、あまり何も考えずに追加の線を引いてみてください。

追加で3本引いてみた。どれも1点では交わっていない。
①、②、③と3本引いてみましたが、どれも交わってませんね。(まぁぶっちゃけ多少は交わらないように意識して引きましたが…)
これ、3本の線を1点でくっつけるって結構難しいんです。
2本の線が交わっている部分に向けて照準を合わせて3本目を引かなくてはならないので当たり前のことですが・・・
何が言いたいかというと、ただでさえ交わることが難しい"3直線が1点で交わる"という奇跡的な出来事か5種類も存在するって三角形ヤバくね?ってことです。
何となく五心の凄さわかっていただけましたかね?
「いや、"三"角形っていうくらいなんだから"3"本の直線に何か特別なことあって当たり前でしょ。」って言われると、うんまぁ、そうなのかもしれませんが。
まぁとにかく皆さんが思っている以上に三角形って特殊な形なのです。
コンビニでおにぎり買うときに「わぁー!これ、奇跡の形じゃん!!」って自然界の神秘に感謝しながら買ってくださいね!
どんなのあったっけ?
「五心」というからには5つあるわけですが、どのようなものがあったか一度思い出してみましょう。
三角形の五心はこちら!
・重心・・・各点から対辺の中点へ降ろした線の交点
・外心・・・各辺の垂直二等分線の交点
・内心・・・各角の二等分線の交点
・垂心・・・各頂点から降ろした垂線の交点
・傍心・・・一つの角の二等分線と残り二角の外角の二等分線の交点
さぁ、覚えていましたかね?
ぶっちゃけ僕は傍心を忘れていました。
まぁ三角形の五心なんて知らなくても普通に生きていけるのでね。
ではでは、それぞれの性質を見ていきましょう。
重心

重心・・・各点から対辺の中点へ降ろした線の交点
性質:重心を通る中線は2:1で内分される
重力的中心
まず一つ目の"心"は重心です。
日常でも使われる言葉なので5つの中では最も知名度が高いと思います。
皆さんご存じの通り、重力の中心となっています。なので"重"心です。
直観的にも「ザ・中心」であり、座標やベクトルで表す時も各点の平均をとったような形をしているので非常に覚えやすいと思います。
さて、この"重心"ですが、肝となる性質は
「各頂点から重心を通る中線はその頂点から対辺までを2:1に内分する」
というものです。
これは重心の存在をベクトルを用いて証明している時に、その過程から導き出されるものです。
"三"角形なので平均をとるときに"3"で割り、そのために内分比は2:1で足すと"3"になる。と覚えると覚えやすいですね。
そして「各頂点とその対辺の中心を結んだ直線」という部分も非常にわかりやすいです。
おそらく皆さんはコロナの自粛期間が明けると毎週のように合コンに繰り出すかと思いますが、その際にコンビニとかで三角くじをもらってこんなネタを用意しておきましょう。
三角くじのそれぞれの辺をちょうど半分の位置で折り目をつけ、辺の中心を見つけます。
次にボールペンを取り出して、それぞれの中心に向かって頂点から線を結んでいきます。
するとそれらの線はある一点で交わるはずです。
その点を今手に持っているボールペンで支えてやると・・・?
これでモテモテですね!
ありがとうございました!
さて、この重心。
バンドメンバーで言うと何でしょう?
さしずめ、最低音のバスドラムを司り、バンドの中心としても位置している「ドラム」といったところでしょうか?
毎週合コンに繰り出している辺りもドラマーっぽいですよね!
外心

外心・・・各辺の垂直二等分線の交点
性質:OA=OB=OC(外心から各頂点までの距離は等しい)
∠BOC=2∠BAC(Oの角度はその奥の頂点の角度の2倍)
外接円の中心
続いては外心です。
「辺を2等分する」という意味で、先ほどの重心と似ていますが、重心は辺の真ん中から頂点に向かって伸びる線、外心は辺の真ん中から垂直に伸びる線という違いがあります。
この些細な違いだけでも、大分と異なった性質の点が導かれます。
さて、この外心。最大の特徴は何といっても"外接円の中心"というところでしょう。
そもそも、外接円の中心だから外心です。
たまたま各辺の垂直二等分線のぶつかった先が外接円の中心になるってロマンありませんか?伝わりませんかね?
さてさて、この外心の性質ですが、やはり何と言ってのその特徴は「外接円の中心」という点でしょう!(点だけに!)
外心の存在は垂直二等分線の性質を最大限に利用してやると見つかります。
↓↓↓興味ある人だけ見てください。↓↓↓
外心まで伸びる線は垂直二等分線なんです。
⇩
垂直二等分線ってことはそこからできる三角形は二等辺三角形になるのです。
⇩
てことは2つの辺が同じ長さになるのです。
⇩
そんな三角形が3つできて、それぞれの二等辺の部分の長さが等しいってそれはもう全ての長さが等しいことになるわけです。
⇩
要するに、Oから各頂点への距離が等しいことになるわけです。
てなわけで「外心から各頂点までの距離が等しい」ことが分かり、それってすなわち「外心は外接円の中心」だということになりますよね?
円周ってどの場所も中心までの距離は等しいはずです。
「東京から半径30km」の円周上って、横浜市もさいたま市も千葉市も東京までの直線距離は30kmのはずです。
東京から半径30kmの円周上の各都市の中で、千葉市だけ直線距離が50kmとかだったら物理法則を捻じ曲げる大発見なので、すぐに学会に報告したほうがいいです。
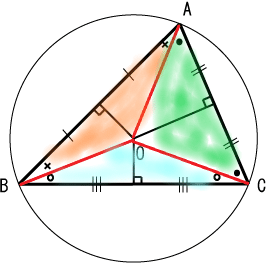
外接円の中心から各頂点へ赤線を引いてみた
上の図を見ての通り、3本の赤線はどれも長さが等しくなります。
⇒Oにコンパスの針を乗せ、Aにコンパスの鉛筆を乗せてぐるっと一回りさせるとBもCも通る円を引けることになりますね。
外接円の中心ってことは芋づる式にいろいろなことが分かります。
まずは先ほどから何度も言っている、中心から各頂点までの距離が等しいということ。
1本の長さが分かれば他2本の長さもわかるのでとっても便利ですね!
そして、円周角の定理を考えれば、∠BOCの角度は∠Aのちょうど2倍だということ。
どっちかの角度が分かれば、それを倍にしたり半分にしたりすることでもう片方の角度もわかってとっても便利ですね!
続いて、二等辺三角形が3つできるという点も重要ポイントです。
(上の図でオレンジ、水色、緑に塗りつぶされた3つ)
下にある2つの角が両方とも同じ角度になりますね。
この性質と、先ほどの「∠BOCの角度は∠Aのちょうど2倍」という性質、あと三角比だとか三角形の内角の和は180°だとかを使えばかなりいろいろな部分の角度が分かってとっても便利ですね!
さて、そんな外心。
バンドメンバーでいうと誰でしょうね?
"外"から見てバンドの中心ってやっぱりボーカルですよね!
なんだかんだ言って歌ってるやつが一番目立つんです!!
内心

内心・・・各角の二等分線の交点
性質:内心から各辺への距離は全て等しい
内接円の中心
お次は内心です。
「二等分線の交点ってさっきと同じやん!!」って思うかもしれませんが、外心は辺の二等分線、内心は角の二等分線です。
辺と角が違うだけで中心もまた異なるのです。

内心から各辺へ無理やり垂直な補助線を引いてやるとその存在を証明できます。この画像で紫色に塗られている線ですね。
外心の時と同様、「中心から距離が等しい」という部分に着目すると、三角形に内接した内接円が作れることもわかります。

ちなみに、上の図で水色に塗られた部分とオレンジに塗られた部分は合同です。だから青い線と赤い線の長さは同じだし、黒い部分の角度も同じです。これ豆知識。
内心って調べてみたんですけどこんなもんなんですよね。
ちょっと地味。
さて、そんな内心。
バンドメンバーでいうと誰でしょう?
"内"から見て中心というとやはりリズム隊の要、ベースといったところでしょうか?
ちょっと地味な感じもピッタシですね!
垂心

垂心・・・各頂点から降ろした垂線の交点
性質:円に内接する四角形が存在する
続いては垂心です。
「あれ?さっきも垂線出てきたじゃん。」と思った方、
先ほど出てきた垂線は外心の「垂直二等分線」です。
辺を二分する垂直な線でしたね。
一方、垂心の垂線は頂点から降ろしただけで、特に二分することはありません。
「あれ?さっきも各頂点から線出てきたじゃん。」と思った方、
先ほど出てきた「各頂点から」は重心(各頂点から辺を二分する線)と内心(角を二分する線)です。
非常にややこしくなってきたので、ここいらでちょっとまとめてみます。

・・・まったくわかりやすくないですね!
話が逸れてしまったので本題に戻りましょう。
一見地味そうな垂心、その性質も意味わかりませんよね。
でも、この垂心、かなりいろいろ使い道があるのです。

垂線の存在を証明する過程で、図のようにたくさんの円を作り出すことができます。
いっぱいありすぎて訳がわからん・・・
("円周角の定理"、"円に内接する四角形の対角の和は180°"を多用することになります)
これ、中に四角形が入っていることわかりますか?

四角形その一

四角形その二
いやぁー、その二はちょっとわかりづらいですね…
辺AB、BC、CAを底辺にしてる台形みたいな四角形なのですが…
実は、その一の四角形たちもその二の四角形たちも円に内接しているのですよ。よく見てみてください。
んで、円に内接しているということは
・向かい合う角の和は180°
・トレミーの定理
・方べきの定理
・ブラーマグプタの定理
これらの定理・性質を使うことができるというわけなのです!!
最後の1個初めて聞いたぞ!!!
垂心が1個あるだけでめちゃくちゃたくさんの角度やら辺の長さやらが判明していくことがわかったと思います!
これは凄いですね!
バンドで言うと、楽器一つながらもエフェクターを駆使して多種多様な音色を作り出すギターのような存在ですね!
様々な音色(性質)を作り出しているのはギター(垂心)だと気づかれないあたりもそっくりで、なんだか同情したくなっちゃいますね!
ちなみに、
ここまで熱心に勉強されてきた皆さんならもうお気づきかもしれませんが、
正三角形は重心、外心、内心、垂心が一致します。
凄いですよね!奇跡です!
コンビニでおにぎり買うときに「わぁー!これ、奇跡の形じゃん!!」って自然界の神秘に感謝しながら買ってくださいね!
傍心

傍心・・・一つの角の二等分線と残りの二角の外角の二等分線の交点
性質:1辺と外角を成している2辺に接した傍接円を描ける
3つの傍心を頂点とした三角形の垂心と元の三角形の内心は等しい
言葉だとうまく説明できないので、図を見てください。

こんな感じで円を描けて、しかも内心になるような直線を引けるよーということです。
直角三角形と角の二等分線の関わりを用いると証明できます。
「角の二等分線」を用いているという関係上、内心と非常に関わりが強いらしく、垂線引くと内心が出てくるのもそのためだと思います。
困ったことに、これといってネタがないのがこの傍心です。
「三角形の五心言ってみて」と聞いて、傍心を答えられる人はかなり少ないのではないでしょうか?
この、非常に影の薄い感じ・・・
まるでキーボードみたいですね・・・
まとめ
ということで、三角形の五心たちを見てきました。
「角を二等分する」とか「垂線を降ろす」とか「辺を二等分する」とか問題によく出てくるフレーズがあるので、それをヒントに
「重心の性質を使うんだ!」とか「内心を利用する問題だな!?」とか思いつくようになれると良いのではないですかね?
ちなみに、バンドマンに変な印象を与えるつもりは全くありません。
バンドっていいですよ!?
みんなも始めてみましょう!
ということで今回はここまで。
今回の記事がためになったという方、面白かったという方はぜひSNS等でシェアしてくださると嬉しいです。
また、「お疲れ!コーヒーでも飲みな!」という方はサポートをしてくださるととても励みになります!
それでは、また次回の記事でお会いしましょう!!
