解析学（微分積分）の深掘り 〜１〜

以前に数学に関して深掘りしたことがありました。数学はシンプルに「解析学」と「代数学」と「幾何学」に分かれます。

私は工学の道に進んだので、数学はある種の道具みたいな見方をしています。それでも、道具として使いこなすには相応の勉強が必要です。

特に解析学は微分積分を中心にかなりの時間をカリキュラムで費やしてきました。その経験は今の仕事に活かされています。

今回は学業から仕事まで数学を使い込んできた者の視点から、解析学すなわち微分積分について、様々な視点から話をしてみたいと思います。まずは、微分積分とは何なのかという話から始めてみましょう。

微分積分の意味

微分積分の理論背景を理解することもだいじですが、まずはそれぞれにどんな意味があるのかをイメージとして掴むことにします。

数学の中でも「人生で何の役に立つのか？」と疑問を呈する最たる存在ですから。親しみやすい内容で導入を作ることにしました。

例として、車の移動を表すモデル（イメージ）を使います。言葉ではこんな感じで微分積分を説明します。

・微分：車のある時刻の瞬間的な位置変化を計算する
・積分：車のある区間の位置変化の累積を計算する

一緒にイメージを示します。ここから微分積分の意味を深掘りをしていきましょう。

微分の詳細について

車が発車する始点Ｏを取ります（始点Ｏの距離はゼロとします）。時刻に対する車の移動した距離の情報が手元にあるとして、ある時刻の車の瞬間的に移動した距離を知りたい。これを求める作業が「微分」です。

微分を大雑把に説明するならば、中学校で学習する「変化の割合」に似ています。

変化の割合は、縦軸（距離）の変化量を横軸（時刻）の変化量で割ることで計算できます。微分とはつまり、一瞬という時間的な変化に対して、距離の変化を計算するということです。

なお、ここでは距離を時間で割るのですから、変化の割合は「速度」に相当することが分かります。

同じく中学校で学習する「等速直線運動」の問題を持ち出します。ここでは、速度は一定の数値（定数）で表されます。また、物体の移動する距離は時刻の１次関数として表されます。

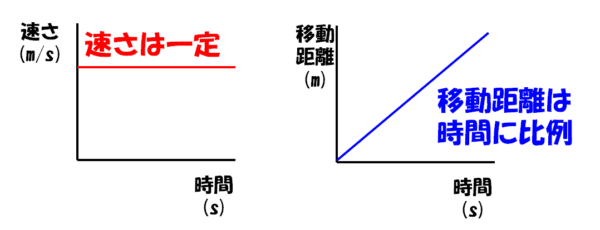
微分は「変化の割合」に似ていると書きました。距離は時刻の１次関数なので、変化の割合は１次関数の比例定数に他なりません。物理的に言えば、この比例定数こそ速度なのです。

以上のことから「距離」の微分とは「速度」と言えることが分かります。

積分の詳細について

一方で、時刻に対する車の速度の情報が手元にあるとして、ある時間的な区間で走行した距離を知りたい。これを求める作業が「積分」です。

積分とはつまり、指定した時間的な区間において瞬間的な位置変化（速度）を足し合わせることです。

別の言い方をすると、縦軸（速度）と横軸（時刻）を設けて速度のグラフを描いたときに、指定した区間でグラフを囲んだ際の面積を求めることです。

再び「等速直線運動」を例に出します。速度のグラフにおいて、始点Ｏ（時刻をゼロとします）からある時刻までの範囲の面積を考えます。この時刻を変数（例えばｘなど）にすると、面積は縦の長さ（速度）と変数ｘの積になります。つまり「速度」を比例定数とした１次関数で「距離」が表現できることが分かります。

これは「速度」の積分が「距離」であることを表しています。そして、これまでの内容から微分と積分が一対の関係にあることも分かります。

微分積分の用語関係

今回は微分積分のイメージを掴んで頂くために、車の移動という形で事例を出しました。ここからは、微分積分で実際に出てくる用語に触れていきます。

時間に対する距離をグラフにしたときの、ある時刻の一瞬の変化の割合（接線の傾きとも言います）を微分係数と言います。特定の地点での速度を意味します。

距離は横軸（時間）の関数です。この関数を微分したときに現れる新たな関数を「導関数」と言います。先ほどの例で言えば、速度を追える関数です。

次に積分について。先ほどは時間的な区間を指定していましたが、このような計算を「定積分」と言います。

区間を変数にする場合（始点Ｏからある時刻の変数ｘまでを設定するなど）、それにより現れる関数を「原始関数」と言い、その作業を「不定積分」と言います。

今回は車の移動というモデル（イメージ）を出しましたが、実際に用語を理解するには、上記のグラフの相互関係を追えている必要があります。

おわりに

今回は初回でもあるので、微分積分の意味から触れてみました。微分積分は物理を定量的（数値として対象を捉えること）に理解するには必須の学問です。

身近な例で言えば、球体の体積を求める場合は、普通ならば公式を持ち出すと思います。ならば、その公式はどこから来たのか。これも微分積分の役割です。

そういうことなどにたくさん触れていけば、微分積分の意味が具体化できるような気がします。

-------------------------

最後まで読んでいただき、ありがとうございます。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに寄り添えたら幸いです。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ プロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎