中学でも分かるガロアの証明⑤正規部分群の縮小について

（復習）左剰余類による類別

　前回までは、３次対称群（３つの文字の入れ替えをすべて集めた群）
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
の正規部分群である、３次交代群（$${S_3}$$ の要素のうち遇置換だけを集めた群）
　$${N=\{id,  \rho_2,  \rho_3\}}$$
による左剰余類（および右剰余類）を考え、その剰余類によって $${S_3}$$ を２つのグループ $${idN,  \tau_1N}$$ に分類しました。

　$${S_3}$$ を、いわゆる回転グループ $${id,  \rho_2,  \rho_3}$$ と、反転グループ $${\tau_1,  \tau_2,  \tau_3}$$ の２つのグループに、要素の数が同じ数（３つ）ずつになるように分けることができます（本シリーズ (30)）。
　なお、一般に３次対称群は $${A_3}$$ と表しますが、ここでは $${S_3}$$ の正規部分群ということで、$${N}$$ という記号で表記しています。normal subgroup（正規部分群）の頭文字です。

（復習）剰余群

　さらに、その左剰余類の集合 $${\{idN,  \tau_1N\}}$$ は、演算
　　$${aN\circ bN=abN}$$
に関して群になります（本シリーズ (31)）。この演算を左剰余類の積という場合があります。
　また、この剰余類の群のことを剰余群といいます（注１）。

　また、右剰余類の集合 $${\{Nid,  N\tau_1\}}$$ も、演算
　　$${Na\circ Na=Nab}$$
に関して群になります。この演算を右剰余類の積という場合があります。

　この左剰余類（および右剰余類）が群になることが、ただの部分群ではなく、正規部分群でなければならない理由です。なお、正規部分群による左剰余類、および右剰余類を、単に剰余類という場合があります。
　一般に、ある部分群が正規部分群であるとき、その剰余類の集合は群（剰余群）となります。正規部分群ではないただの部分群だと、その剰余類の集合は群にはなりません（本シリーズ (31)）。

３次交代群をさらに類別する

　ここではさらに、$${S_3}$$ の正規部分群である３次交代群
　$${N=\{id,  \rho_2,  \rho_3\}}$$
について、さらにその正規部分群を考え、それによる左剰余類（および右剰余類）の集合が群になることを示していきます。

　まず、$${N=\{id,  \rho_2,  \rho_3\}}$$ の正規部分群は次の２つのみです。
　$${\{id\}}$$
　$${\{id,  \rho_2,  \rho_3\}}$$
いわゆる単位元だけからなる集合と、自分自身です。この２つはすべての群の正規部分群となるので自明な正規部分群といいます。
　なお、$${N}$$ の部分群も
　$${\{id\}}$$
　$${\{id,  \rho_2,  \rho_3\}}$$
であり、$${N}$$ の部分群は、同時に正規部分群でもあります。
　$${\{\rho_2\}}$$
　$${\{id,  \rho_2\}}$$
　$${\{\rho_2,  \rho_3\}}$$
などは、そもそも $${N}$$ の部分群ではありません。

真部分集合について

　それでは、単位元だけからなる正規部分群を
　$${I=\{id\}}$$
とおき、それによる左剰余類と右剰余類を求めていきます。
　なお、部分集合であって、もとの集合と一致しないものを真部分集合といいます（注２）。$${\{id\}}$$ は $${N}$$ の真部分集合となりますが、自分自身 $${\{id,  \rho_2,  \rho_3\}}$$ は $${N}$$ の真部分集合ではありません。

　$${\{id\}}$$ は $${N}$$ の真部分集合である
　$${\{id,  \rho_2,  \rho_3\}}$$ は $${N}$$ の真部分集合ではない

　正規部分群による剰余類を考えるにあたっては、真部分集合となる正規部分群を考えることに意味を持ちます（注３）。

　さて、$${I=\{id\}}$$ による左剰余類とは、$${I}$$ に $${N=\{id,  \rho_2,  \rho_3\}}$$ の要素 $${id,  \rho_2,  \rho_3}$$ のすべてを左から作用させた
　$${idI,  \rho_2I,  \rho_3I}$$
のそれぞれを指します。
　同様に $${I}$$ による右剰余類とは、$${I}$$ に $${N}$$ の要素すべてを右から作用させた
　$${Iid,  I\rho_2,  I\rho_3}$$
のそれぞれを指します。
　まずは復習として
　$${idI=Iid}$$
　$${\rho_2I=I\rho_2}$$
　$${\rho_3I=I\rho_3}$$
をすべて満たすことによって、$${I}$$ が正規部分群の定義を満たすことを確認します。
　なお、正規部分群の定義は次のものでした。

（復習）正規部分群の定義

　$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について

$$
\begin{align*}
gN=Ng
\end{align*}
$$

を満たすとき、$${N}$$ を $${G}$$ の正規部分群という。

＊＊＊

　まず、３次対称群 $${N=\{id,  \rho_2,  \rho_3\}}$$ の要素について、その置換の合成の演算表は次のようになります（本シリーズ (29)）。なお、この置換の合成を置換の積という場合があります。

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
    & \utilde{\underline{id}} & \rho_2 & \rho_3\\ \hline\hline
\underline{id} & \underline{id} & \rho_2 & \rho_3\\ \hline
\utilde{\rho_2} & \utilde{\rho_2} & \rho_3 & id\\ \hline
\rho_3 & \rho_3 & id & \rho_2
\end{array}
$$

すると、下線部より
　$${idid=id　\cdots (*1)}$$

また、波線部より
　$${\rho_2id=\rho_2　\cdots (*2)}$$

以下同様にして
　$${id\rho_2=\rho_2　\cdots (*3)}$$
　$${\rho_3id=\rho_3　\cdots (*4)}$$
　$${id\rho_3=\rho_3　\cdots (*5)}$$

(1a)　左から $${id}$$ を作用させる。

$$
\begin{align*}
idI&=id\{id\}\\
&=\{idid\}\\
&=\{id\}　\because  (*1)  より\\
\end{align*}
$$

(1b)　右から $${id}$$ を作用させる。

$$
\begin{align*}
Iid&=\{id\}id\\
&=\{idid\}\\
&=\{id\}　\because  (*1)  より\\
\end{align*}
$$

(1a)、(1b) より

$$
\begin{align*}
idI=Iid=\{id\}
\end{align*}
$$

(2a)　左から $${\rho_2}$$ を作用させる。

$$
\begin{align*}
\rho_2I&=\rho_2\{id\}\\
&=\{\rho_2id\}\\
&=\{\rho_2\}　\because  (*2)  より\\
\end{align*}
$$

(2b)　右から $${\rho_2}$$ を作用させる。

$$
\begin{align*}
I\rho_2&=\{id\}\rho_2\\
&=\{id\rho_2\}\\
&=\{\rho_2\}　\because  (*3)  より\\
\end{align*}
$$

(2a)、(2b) より

$$
\begin{align*}
\rho_2I=I\rho_2=\{\rho_2\}
\end{align*}
$$

(3a)　左から $${\rho_3}$$ を作用させる。

$$
\begin{align*}
\rho_3I&=\rho_3\{id\}\\
&=\{\rho_3id\}\\
&=\{\rho_3\}　\because  (*4)  より\\
\end{align*}
$$

(3b)　右から $${\rho_3}$$ を作用させる。

$$
\begin{align*}
I\rho_3&=\{id\}\rho_3\\
&=\{id\rho_3\}\\
&=\{\rho_3\}　\because  (*5)  より\\
\end{align*}
$$

(3a)、(3b) より

$$
\begin{align*}
\rho_3I=I\rho_3=\{\rho_3\}
\end{align*}
$$

　以上により
　$${idI=Iid}$$
　$${\rho_2I=I\rho_2}$$
　$${\rho_3I=I\rho_3}$$
をすべて満たすので、単位元だけからなる部分群 $${I}$$ は正規部分群であることが分かります。

 　これにより、正規部分群 $${A_3}$$ を、３つの左剰余類
　$${idI=\{id\}}$$
　$${\rho_2I=\{\rho_2\}}$$
　$${\rho_3I=\{\rho_3\}}$$
で類別することができました。

　さらに、$${I}$$ による左剰余類の集合
　$${\{idI,  \rho_2I,  \rho_3I\}}$$
は、演算
　$${aI\circ bI=abI}$$
に関して群（剰余群）になります。以下、その証明を簡単に述べていきます。

　左剰余類 $${idI,  \rho_2I,  \rho_3I}$$ 同士の積の演算表は次の通りです。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \rho_2I & \rho_3I\\ \hline\hline
idI & idI & \rho_2I & \rho_3I\\ \hline
\rho_2I & \rho_2I & \rho_3I & idI\\ \hline
\rho_3I & \rho_3I & idI & \rho_2I
\end{array}
$$

　証明は本シリーズ (31) でやった、$${N}$$ による左剰余類の集合 $${\{idN,  \tau_1N\}}$$ が群になる証明と同じです。

Ｉ による左剰余類の集合が群になることの証明

　まず、群の定義を復習します。

（復習）群の定義

　空でない集合 $${G}$$ の任意の要素 $${a,  b,  c}$$ の間に１つの演算 $${*}$$ が規定されているとする。
　この集合 $${G}$$ の任意の要素 $${a,  b,  c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1)　$${a*b}$$ は $${G}$$ の要素である。
(2)　交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3)　$${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4)　$${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。

＊＊＊

(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。この要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元になるような要素の存在です。この要素を逆元といいます。
　単なる集合（要素の集まり）ではなく、集合の要素に、上記の演算規則 (1)～(4) が規定された集合が群です。

　要するに群とは、イメージとして
(1)　全部そろっている
(2)　つなげることができる
(3)　変えないことができる
(4)　元に戻すことができる
の、４つの条件が成り立つものの集まり（集合）です。

群であることの証明

　さて、$${I}$$ による左剰余類の集合
　$${\{idI,  \rho_2I,  \rho_3I\}}$$
は、演算
　$${aI\circ bI=abI}$$
に関して群になることを、上の群の定義 (1) ～ (4) に沿って、次の左剰余類同士の積の演算表を利用して簡単に証明していきます。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \rho_2I & \rho_3I\\ \hline\hline
idI & \underline{idI} & \rho_2I & \rho_3I\\ \hline
\rho_2I & \utilde{\underline{\rho_2I}} & \utilde{\rho_3I}
& \utilde{idI}\\ \hline
\rho_3I & \underline{\rho_3I} & idI & \rho_2I
\end{array}
$$

(1)　演算 о に関して閉じている。

　これは、どの縦の列（例えば上表の下線部）をみても、どの横の列（例えば上表の波線部）をみても、$${idI,  \rho_2I,  \rho_3I}$$ が１個ずつ、すべて現れていることから分かります。

(2)　交換法則が成り立つ。

　代表として
　$${(idI\circ\rho_2I)\circ\rho_3I=idI\circ(\rho_2I\circ\rho_3I)}$$
を示します。他の組み合わせも同様です。
　左剰余類同士の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \underline{idI} & \utilde{\rho_2I} & \underlinesegment{\rho_3I}\\ \hline\hline
\utilde{\underline{idI}} & \underline{idI} & \utilde{\rho_2I} & \rho_3I\\ \hline
\underlinesegment{\rho_2I} & \rho_2I & \rho_3I & \underlinesegment{idI}\\ \hline
\rho_3I & \rho_3I & idI & \rho_2I
\end{array}
$$

より

　$${idI\circ idI=idI　\cdots (*6)}$$（下線部）
　$${idI\circ \rho_2I=\rho_2I　\cdots (*7)}$$（波線部）
　$${\rho_2I\circ \rho_3I=idI　\cdots (*8)}$$（$${\scriptsize \hspace{-2pt}\vdash\hspace{-1pt}\raisebox{2.5pt}{\text{\textunderscore}}\hspace{-1pt}\dashv\hspace{-1pt}}$$ 線部）

なので、カッコから先に計算して

$$
\begin{align*}
（左辺）&=\underset{先に計算}{(\underline{idI\circ\rho_2I})}\circ\rho_3I\\
&=\rho_2I\circ\rho_3I　{\small (*7) より}\\
&=idI　\hspace{24pt}{\small (*8) より}
\end{align*}
$$

$$
\begin{align*}
（右辺）&=idI\circ(\underset{先に計算}{\underline{\rho_2I\circ\rho_3I}})\\
&=idI\circ idI　{\small (*8) より}\\
&=idI　\hspace{24pt}{\small (*6) より}
\end{align*}
$$

よって、（左辺）$${=}$$（右辺）となり証明された。

(3)　単位元は存在する。

　左剰余類同士の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \rho_2I & \rho_3I\\ \hline\hline
idI & \underline{idI} & \utilde{\rho_2I} & \underlinesegment{\rho_3I}\\ \hline
\rho_2I & \utilde{\rho_2I} & \rho_3I & idI\\ \hline
\rho_3I & \underlinesegment{\rho_3I} & idI & \rho_2I
\end{array}
$$

より
　$${idI\circ idI=idI}$$（下線部）
　$${\rho_2I\circ idI=idI\circ\rho_2I=\rho_2I}$$（波線部）
　$${\rho_3I\circ idI=idI\circ\rho_3I=\rho_3I}$$（$${\scriptsize \hspace{-2pt}\vdash\hspace{-1pt}\raisebox{2.3pt}{\text{\textunderscore}}\hspace{-1pt}\dashv\hspace{-1pt}}$$ 線部）
をすべて満たすので、単位元は $${idI}$$ となります。

(4)　逆元は存在する。

　左剰余類同士の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \rho_2I & \rho_3I\\ \hline\hline
idI & \underline{idI} & \rho_2I & \rho_3I\\ \hline
\rho_2I & \rho_2I & \rho_3I & \utilde{idI}\\ \hline
\rho_3I & \rho_3I & \utilde{idI} & \rho_2I
\end{array}
$$

から
　$${idI\circ idI=idI}$$（下線部）
より
　$${idI}$$ の逆元は $${idI}$$
また
　$${\rho_2I\circ\rho_3I=\rho_3l\circ\rho_2l=idI}$$（波線部）
より
　$${\rho_2I}$$ の逆元は $${\rho_3I}$$
　$${\rho_3I}$$ の逆元は $${\rho_2I}$$
となります。

　これで、$${I}$$ による左剰余類の集合
　$${\{idI,  \rho_2I,  \rho_3I\}}$$
は、演算
　$${aI\circ bI=abI}$$
に関して群になることが証明されました。つまり、左剰余類の集合 $${\{idI,  \rho_2I,  \rho_3I\}}$$ は剰余群です。

右剰余類の集合も群になる 

　なお、左剰余類と同様に右剰余類を考えることができ、その集合
　$${\{Iid,  I\rho_2,  I\rho_3\}}$$
も、演算
　$${Ia\circ Ib=Iab}$$
に関して群になります。つまり、右剰余類の集合 $${\{Iid,  I\rho_2,  I\rho_3\}}$$ も剰余群です。

　演算表は次の通りです。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & Iid & I\rho_2 & I\rho_3\\ \hline\hline
Iid & Iid & I\rho_2 & I\rho_3\\ \hline
I\rho_2 & I\rho_2 & I\rho_3 & Iid\\ \hline
I\rho_3 & I\rho_3 & Iid & I\rho_2
\end{array}
$$

　一般に、正規部分群による左剰余類の集合、または右剰余類の集合は、上で述べたように演算を定義することによって、どちらも群（剰余群）となります。
　さらに、左剰余類の類別と右剰余類の類別は、同じ類別となることも確認できます。

＜左剰余類による類別＞

$${\hspace{82pt}\Updownarrow}$$  類別の方法は同じ

＜右剰余類による類別＞

　一般に、ある部分群が正規部分群のとき、その正規部分群による「左剰余類による類別」と「右剰余類による類別」は等しくなります。また逆に、ある部分群による「左剰余類による類別」と「右剰余類による類別」が等しいとき、その部分群は正規部分群となります（本シリーズ (30)）。

$$
\begin{align*}
&正規部分群\\
\rightleftarrows  &「左剰余類による類別」と「右剰余類による類別」\\
&は等しい  \cdots (*5)
\end{align*}
$$

ガロアによる”正規部分群”の定義

　ガロアによれば、上記の $${(*5)}$$ を「正規部分群の定義」としています（参考『ガロア理論超入門』小林吹代著 他）。
　正規部分群という言葉は当時はまだなかったため、ガロアは $${(*5)}$$ を満たすことを「固有の分解」と表現しています。この「固有の分解」をもたらす部分群が、今の言葉でいう正規部分群となります。

今までの流れを整理

 　ここで、改めて今までの流れを整理すると、３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
を始めとして、正規部分群による剰余群を次々と構成していくことによって
　$${S_3 \xrightarrow[縮小]{} N \xrightarrow[縮小]{} I}$$
と、恒等置換 $${id}$$ のみの集合 $${I}$$ にまで「正規部分群が縮小」されていく、次の (step1),  (step2) の過程がみてとれます。

(step1)　$${S_3}$$ から $${N}$$ へ縮小
　３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
の正規部分群
　$${N=\{id,  \rho_2,  \rho_3\}}$$
による左剰余類の集合 $${\{idN,  \tau_2N\}}$$ は剰余群になる。

$$
\begin{align*}
&\hspace{43.8pt}\underline{\footnotesize \hspace{16.6pt}剰余群\hspace{16.5pt}}\\[-6pt]
\{idN,  \tau_1N\}&=\{\overset{\downarrow}{\underset{idN}{\underline{\{id,  \rho_2,  \rho_3\}}}},  \overset{\downarrow}{\underset{\tau_1N}{\underline{\{\tau_1,  \tau_2,  \tau_3\}}}}\}
\end{align*}
$$

(step2)　$${N}$$ から $${I}$$ へ縮小
　$${N=\{id,  \rho_2,  \rho_3\}}$$
の正規部分群
　$${I=\{id\}}$$
による左剰余類の集合 $${\{idI,  \rho_2I,  \rho_3I\}}$$ は剰余群になる。

$$
\begin{align*}
&\hspace{27.5pt}\underline{\footnotesize \hspace{14pt}剰余群\hspace{14pt}}\\[-6pt]
\{idI,  \rho_2I,  \rho_3I\}&=\{\overset{\downarrow}{\underset{idI}{\underline{\{id\}}}},  \overset{\downarrow}{\underset{\rho_2I}{\underline{\{\rho_2\}}}},  \overset{\downarrow}{\underset{\rho_3I}{\underline{\{\rho_3\}}}}\}\\
\end{align*}
$$

　つまり

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は群\\[10pt]
縮小  &\downarrow  {\small 正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{-19pt}剰余群  \{idN,  \tau_1N\}  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}\\[10pt]
縮小  &\downarrow  {\small \hspace{-26pt}正規部分群  I=\{id\}  による \atop 剰余群  \{idI,  \rho_2I,  \rho_3I\}  が構成可能}\\[12pt]
I&=\{id\}
\end{align*}
$$

　そしてこれは、アーベルの証明の時に解説した、３次方程式における「累乗根の添加による（解の置換の）対称性の破壊」と、類似の過程をたどっています（本シリーズ (18), (19) 他） 。

ガロアとアーベルの対応

アーベルの証明（本シリーズ (19) より加筆して抜粋）

$$
\begin{gather*}
Q(\omega)\\[2pt]
\hspace{67pt}\downarrow  \Leftarrow  X_3  の添加\\[2pt]
Q(\omega,  X_3)\\[2pt]
\hspace{63pt}\downarrow  \Leftarrow  A  の添加\\[2pt]
Q(\omega,  X_3,  A)
\end{gather*}
\hspace{10pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
\underset{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3  で不変}{\bf ３次置換で不変（対称式）}\\
\hspace{67pt}\downarrow  \Leftarrow  X_3  の添加\\
\underset{id,  \rho_2,  \rho_3  のみで不変}{\bf 遇置換シンメトリー}\\
\hspace{63pt}\downarrow  \Leftarrow  A  の添加\\
\underset{id  のみで不変}{\bf 恒等置換のみで不変}
\end{gather*}
$$

　３次方程式の解の公式は、集合 $${Q(\omega,  X_3,  A)}$$ 内で構成できることはすでにやりました（本シリーズ (12), (13), (26), (27)）。
　アーベルの証明でいうところの「累乗根の添加による（解の置換の）対称性の破壊」が、ガロアによる「群の構造」と関連付けられていることに着目してください（注４）。

$$
\begin{gather*}
\underset{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3  で不変}{\bf ３次置換で不変（対称式）}\\
\hspace{67pt}\downarrow  \Leftarrow  X_3  の添加\\
\underset{id,  \rho_2,  \rho_3  のみで不変}{\bf 遇置換シンメトリー}\\
\hspace{63pt}\downarrow  \Leftarrow  A  の添加\\
\underset{id  のみで不変}{\bf 恒等置換のみで不変}
\end{gather*}
\hspace{-2pt}
\xleftrightarrow[対応]{}
\hspace{-10pt}
\begin{gather*}
\hspace{6pt}S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は群\\
\hspace{36pt}\downarrow  \Leftarrow  {\footnotesize 剰余群  \{idN,  \tau_1N\} \atop \hspace{-29pt}を構成可能}\\
N=\{id,  \rho_2,  \rho_3\}  は正規部分群\\
\hspace{50pt}\downarrow  \Leftarrow  {\footnotesize 剰余群  \{idI,  \rho_2I,  \rho_3I\} \atop \hspace{-40pt}を構成可能}\\
\hspace{-24pt}I=\{id\}  は正規部分群
\end{gather*}
$$

　ガロアの発見の核心は、解の公式に使える式を

　$${Q(\omega) \xrightarrow[X_3  の添加]{} Q(\omega,  X_3) \xrightarrow[A  の添加]{} Q(\omega,  X_3,  A)}$$

と拡大するにつれて、対応する群が

　$${S_3 \xrightarrow[正規部分群を取る]{} N \xrightarrow[正規部分群を取る]{} I}$$

と、$${S_3}$$ の部分群のうち「正規部分群」を次々と取りながら縮小されていくことにあります。
　これを包含関係の記号 $${\subset,  \supset}$$ を用いて表すと、次のようになります（本シリーズ (29)）（注２）。
　$${Q(\omega) \subset Q(\omega,  X_3) \subset Q(\omega,  X_3,  A)}$$
　$${S_3 \supset N \supset I}$$
一方が拡大、一方が縮小と、ちょうど逆の関係になります。

$$
\begin{gather*}
Q(\omega)\\[2pt]
\hspace{41pt}拡大  \downarrow  \Leftarrow  X_3  の添加\\[2pt]
Q(\omega,  X_3)\\[2pt]
\hspace{37pt}拡大  \downarrow  \Leftarrow  A  の添加\\[2pt]
Q(\omega,  X_3,  A)
\end{gather*}
\hspace{-2pt}
\xleftrightarrow[対応]{}
\hspace{-10pt}
\begin{gather*}
\hspace{6pt}S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は群\\
\hspace{15pt}縮小\downarrow  \Leftarrow  {\footnotesize 剰余群  \{idN,  \tau_1N\} \atop \hspace{-29pt}を構成可能}\\
N=\{id,  \rho_2,  \rho_3\}  は正規部分群\\
\hspace{28pt}縮小\downarrow  \Leftarrow  {\footnotesize 剰余群  \{idI,  \rho_2I,  \rho_3I\} \atop \hspace{-40pt}を構成可能}\\
\hspace{-24pt}I=\{id\}  は正規部分群
\end{gather*}
$$

　$${X_3}$$ は解の差積でした。つまり
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
　すると、$${(X_3)^2}$$ は対称式なので、集合 $${Q(\omega)}$$ 内で構成できますが、その「平方根」である $${X_3}$$ は $${Q(\omega)}$$ 内で構成できません（本シリーズ (12)）。
　よって、$${Q(\omega)}$$ に $${X_3}$$ を添加して使える式の集合を $${Q(\omega,  X_3)}$$ に拡大しますが、ガロアによると、それは剰余群 $${\{idN,  \tau_1N\}}$$ が構成できることに対応しています。
　さらに、$${A}$$ はラグランジュ・リゾルベントでした。つまり
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
　すると、$${A^3}$$ は遇置換シンメトリーをもつので、集合 $${Q(\omega,  X_3)}$$ 内で構成できますが、その「３乗根」である $${A}$$ は $${Q(\omega,  X_3)}$$ 内で構成できません（本シリーズ (12), (13)）。
　よって、$${Q(\omega,  X_3)}$$ に $${A}$$ を添加して使える式の集合を $${Q(\omega,  X_3,  A)}$$ に拡大しますが、ガロアによると、それは剰余群 $${\{idI,  \rho_2I,  \rho_3I\}}$$ が構成できることに対応します。
　さらに言えば、次の章で詳しく述べますが、剰余群
　$${\{idN,  \tau_1N\}}$$
　$${\{idI,  \rho_2I,  \rho_3I\}}$$
は巡回群といわれるものです。要素の個数に応じて
　$${\{idN,  \tau_1N\}}$$ は２次巡回群
　$${\{idI,  \rho_2I,  \rho_3I\}}$$ は３次巡回群
となります。
　２次巡回群 $${\{idN,  \tau_1N\}}$$ が構成できることは、平方根（２乗恨）を添加することに対応し、３次巡回群 $${\{idI,  \rho_2I,  \rho_3I\}}$$ が構成できることは、３乗根の添加に対応しています。つまり、「２次」と「２乗恨」、「３次」と「３乗根」が対応します。

$$
\begin{align*}
\bm{２}次巡回群の構成 &\xleftrightarrow[対応]{} 平方根（\bm{２}乗恨）の添加\\
\bm{３}次巡回群の構成 &\xleftrightarrow[対応]{} \bm{３}乗恨の添加\\
\end{align*}
$$

　平たく言えば、「正規部分群の縮小の列が、この対応関係を保持しながら、単位元のみからなる正規部分群 $${\{id\}}$$ にうまくたどり着くことができれば、その方程式には解の公式が存在する。逆に $${\{id\}}$$ にたどり着かなければ、解の公式は存在しない」というのがガロアのアイデアです。
　巡回群、およびそれを用いたガロアのアイデアについて、次の章以降から順を追って解説していきます。

（注１）集合を要素に持つ集合

　左剰余類の集合 $${\{idN,  \tau_1N\}}$$ は、「集合を要素に持つ集合」であることに注意してください。$${\{idN,  \tau_1N\}}$$ の要素は $${idN,  \tau_1N}$$ ですが、それは
　$${idN=\{id,  \rho_2,  \rho_3\}}$$
　$${\tau_1N=\{\tau_1,  \tau_2,  \tau_3\}}$$
という集合でした。すなわち、左剰余類の集合は
　$${\{idN,  \tau_1N\}=\{\{id,  \rho_2,  \rho_3\},  \{\tau_1,  \tau_2,  \tau_3\}\}}$$
という「集合を要素に持つ集合」となります。

$$
\{idN,  \tau_1N\}=\{\underset{要素が集合}{\underline{\{id,  \rho_2,  \rho_3\}}},  \underset{要素が集合}{\underline{\{\tau_1,  \tau_2,  \tau_3\}}}\}
$$

　つまり、３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
は群であり、その正規部分群
　$${N=\{id,  \rho_2,  \rho_3\}}$$
によって類別された左剰余類の集合
　$${\{idN,  \tau_1N\}=\{\{id,  \rho_2,  \rho_3\},  \{\tau_1,  \tau_2,  \tau_3\}\}}$$
について、その要素である
　$${idN=\{id,  \rho_2,  \rho_3\}}$$
　$${\tau_1N=\{\tau_1,  \tau_2,  \tau_3\}}$$
という「集合」が、$${aN\circ bN=abN}$$ という演算に関して「一体」となって群（剰余群）となる、というのがガロアの発見であり、正規部分群が重要である理由です。

$$
\begin{align*}
&\hspace{43.8pt}\underline{\footnotesize \hspace{16.6pt}剰余群\hspace{16.5pt}}\\[-6pt]
\{idN,  \tau_1N\}&=\{\overset{\downarrow}{\underset{idN}{\underline{\{id,  \rho_2,  \rho_3\}}}},  \overset{\downarrow}{\underset{\tau_1N}{\underline{\{\tau_1,  \tau_2,  \tau_3\}}}}\}
\end{align*}
$$

（注２）部分集合について（復習）

　本シリーズ (29)でやったことの復習です。
　例えば、２つの集合
　$${\text{P}=\{2,  4\}}$$
　$${\text{Q}=\{1,  2,  3,  4,  5\}}$$
について、この２つの集合の関係をベン図で描くと、次のようになります。

　この図から分かるように、$${\text{P}}$$ は $${\text{Q}}$$ に含まれています。これを記号で次のように書きます。

$$
\begin{align*}
\text{P}\subset\text{Q}　または　\text{Q}\supset\text{P}
\end{align*}
$$

　このとき、$${\text{P}}$$ は $${\text{Q}}$$ の部分集合といいます。大きい方に開いていると覚えます。２つの集合の一方が他方の部分集合であるとき、この２つの集合の間に包含関係があるといいます。
　また、上記の例では、$${\text{P}}$$ と $${\text{Q}}$$ は一致していません。明らかに $${\text{P}}$$ の要素は $${\text{Q}}$$ の（全部ではなく）一部分となっています。このとき $${\text{P}}$$ は $${\text{Q}}$$ の真部分集合といいます。
　自分自身である $${\text{Q}}$$ は $${\text{Q}}$$ の部分集合ではあるが、真部分集合ではありません。

　部分群 $${\text{P}}$$ は $${\text{Q}}$$ の真部分集合である。
　部分群 $${\text{Q}}$$ は $${\text{Q}}$$ の真部分集合ではない。

（注３）自分自身の左剰余類（または右剰余類）を求める

　本文では、$${N=\{id,  \rho_2,  \rho_3\}}$$ の正規部分群 $${I=\{id\}}$$ について、それによる左剰余類（および右剰余類）を考えました。
　ここでは練習として、$${N}$$ の正規部分群 $${N}$$ について、それによる左剰余類（および右剰余類）を考えてみましょう。つまり、正規部分群として自分自身 $${N}$$ を取ってみます。

　$${N=\{id,  \rho_2,  \rho_3\}}$$ による左剰余類とは、$${N}$$ に $${N}$$ の要素
　$${id,  \rho_2,  \rho_3}$$
のすべてを左から作用させた
　$${idN,  \rho_2N,  \rho_3N}$$
のそれぞれを指します。
　同様に $${N}$$ による右剰余類とは、$${N}$$ に $${N}$$ の要素すべてを右から作用させた
　$${Nd,  N\rho_2,  N\rho_3}$$
のそれぞれを指します。
　まずは復習として
　$${idN=Nid}$$
　$${\rho_2N=N\rho_2}$$
　$${\rho_3N=N\rho_3}$$
のすべて満たすことによって、$${N}$$ が正規部分群の定義を満たすことを確認します。

　まず
　$${N=\{id,  \rho_2,  \rho_3\}}$$ の要素について、その置換の合成の演算表は次のようになります（本シリーズ (29)）。なお、この置換の合成を置換の積という場合があります。

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
    & \utilde{\underline{id}} & \rho_2 & \rho_3\\ \hline\hline
\underline{id} & \underline{id} & \rho_2 & \rho_3\\ \hline
\utilde{\rho_2} & \utilde{\rho_2} & \rho_3 & id\\ \hline
\rho_3 & \rho_3 & id & \rho_2
\end{array}
$$

　すると、下線部より
　$${idid=id　\cdots (*1)}$$

また、波線部より
　$${\rho_2id=\rho_2　\cdots (*2)}$$

以下同様にして
　$${id\rho_2=\rho_2　\cdots (*3)}$$
　$${\rho_3id=\rho_3　\cdots (*4)}$$
　$${id\rho_3=\rho_3　\cdots (*5)}$$

(1a)　左から $${id}$$ を作用させる。

$$
\begin{align*}
idN&=id\{id,  \rho_2,  \rho_3\}\\
&=\{idid,  id\rho_2,  id\rho_3\}\\
&=\{id,  \rho_2,  \rho_3\}　\because  (*1),  (*3),  (*5)  より
\end{align*}
$$

(1b)　右から $${id}$$ を作用させる。

$$
\begin{align*}
Nid&=\{id,  \rho_2,  \rho_3\}id\\
&=\{idid,  \rho_2id,  \rho_3id\}\\
&=\{id,  \rho_2,  \rho_3\}　\because  (*1),  (*2),  (*4)  より
\end{align*}
$$

(1a)、(1b) より

$$
\begin{align*}
idN=Nid=\{id,  \rho_2,  \rho_3\}
\end{align*}
$$

以下同様にして

(2a)　左から $${\rho_2}$$ を作用させる。

$$
\begin{align*}
\rho_2N&=\rho_2\{id,  \rho_2,  \rho_3\}\\
&=\{\rho_2id,  \rho_2\rho_2,  \rho_2\rho_3\}\\
&=\{\rho_2,  \rho_3,  id\}\\
&=\{id,  \rho_2,  \rho_3\}　(*)
\end{align*}
$$

　$${(*)}$$  集合はものの集まりなので、要素を並べる順を変えても同じ集合です。

(2b)　右から $${\rho_2}$$ を作用させる。

$$
\begin{align*}
N\rho_2&=\{id,  \rho_2,  \rho_3\}\rho_2\\
&=\{id\rho_2,  \rho_2\rho_2,  \rho_3\rho_2\}\\
&=\{\rho_2,  \rho_3,  id\}\\
&=\{id,  \rho_2,  \rho_3\}
\end{align*}
$$

(2a)、(2b) より

$$
\begin{align*}
\rho_2N=N\rho_2=\{id,  \rho_2,  \rho_3\}
\end{align*}
$$

(3a)　左から $${\rho_3}$$ を作用させる。

$$
\begin{align*}
\rho_3N&=\rho_3\{id,  \rho_2,  \rho_3\}\\
&=\{\rho_3id,  \rho_3\rho_2,  \rho_3\rho_3\}\\
&=\{\rho_3,  id,  \rho_2\}\\
&=\{id,  \rho_2,  \rho_3\}
\end{align*}
$$

(3b)　右から $${\rho_3}$$ を作用させる。

$$
\begin{align*}
N\rho_3&=\{id,  \rho_2,  \rho_3\}\rho_3\\
&=\{id\rho_3,  \rho_2\rho_3,  \rho_3\rho_3\}\\
&=\{\rho_3,  id,  \rho_2\}\\
&=\{id,  \rho_2,  \rho_3\}
\end{align*}
$$

(3a)、(3b) より

$$
\begin{align*}
\rho_3N=N\rho_3=\{id,  \rho_2,  \rho_3\}
\end{align*}
$$

　よって
　$${idN=Nid}$$
　$${\rho_2N=N\rho_2}$$
　$${\rho_3N=N\rho_3}$$
をすべて満たすので、自分自身である部分群 $${N}$$ は正規部分群であることが分かります。
 　しかし、$${N}$$ による左剰余類は
　$${idN=\rho_2N=\rho_3N=\{id,  \rho_2,  \rho_3\}}$$
となるが、これは集合としては、自分自身である正規部分群
　$${N=\{id,  \rho_2,  \rho_3\}}$$
と同じなので、$${N}$$ は類別されていないことが分かります。

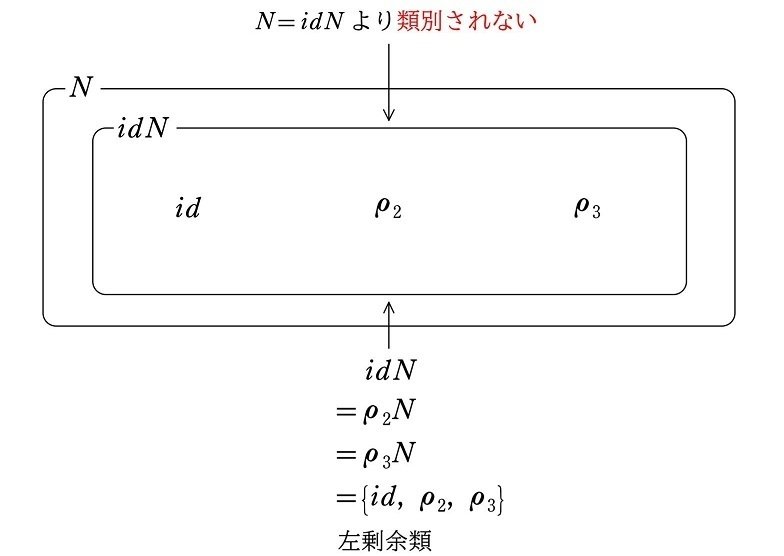
　正規部分群による左剰余類（および右剰余類）を考えるにあたっては、それによってもとの群が２つ以上に類別されることに意味を持ちます。
　なお、本文の $${I}$$ による左剰余類（および右剰余類）では、それによって $${N}$$ は $${idI,  \rho_2I,  \rho_3I}$$ の３つに類別されます

（注４）平方根と３乗根の添加

　$${X_3}$$ を添加することは、平方根 $${\sqrt{(X_3)^2}}$$ を添加することと同じであり、$${A}$$ を添加することは、３乗根 $${\sqrt[3]{A^3}}$$ を添加することと同じなので、次の等式が成り立ちます（本シリーズ (13)）。
　$${Q(\omega,  X_3)=Q(\omega,  \sqrt{(X_3)^2})}$$
　$${Q(\omega,  X_3,  A)=Q(\omega,  \sqrt{(X_3)^2},  \sqrt[3]{A^3})}$$
　よって、本シリーズでは次のように表記している場合もあります。

$$
\begin{gather*}
Q(\omega)\\[2pt]
\hspace{77pt}\downarrow  \Leftarrow  \sqrt{(X_3)^2}  の添加\\[2pt]
Q(\omega,  \sqrt{(X_3)^2})\\[2pt]
\hspace{63pt}\downarrow  \Leftarrow  \sqrt[3]{A^3}  の添加\\[2pt]
Q(\omega,  \sqrt{(X_3)^2},  \sqrt[3]{A^3})
\end{gather*}
\hspace{0pt}
\xleftrightarrow[対応]{}
\hspace{-25pt}
\begin{gather*}
\underset{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3  で不変}{\bf ３次置換で不変（対称式）}\\
\hspace{67pt}\downarrow  \Leftarrow  \sqrt{(X_3)^2}  の添加\\
\underset{id,  \rho_2,  \rho_3  のみで不変}{\bf 遇置換シンメトリー}\\
\hspace{63pt}\downarrow  \Leftarrow  \sqrt[3]{A^3}  の添加\\
\underset{id  のみで不変}{\bf 恒等置換のみで不変}
\end{gather*}
$$

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、および「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について簡単に解説
（29）中学でも分かるガロアの証明①　ガロアの発見した「部分群」について簡単に解説
（30）中学でも分かるガロアの証明③　ガロアの発見した「正規部分群」について
（31）中学でも分かるガロアの証明④　ガロアの発見した「剰余群」について