近似とテイラー展開

　大学の数学で、テイラー展開(マクローリン展開)というものをならった。なにやら複雑そうな式がつづき、そもそもなんのために存在するのやら、意味がわからなかった。
　文系だったので、高校数学もよく知らないまま、いきなりこういう式を見てもわからないのは、当然だった。
　大学を卒業したあとに、せめて高校レベルの数学くらいは理解したいと、高校の受験参考書を読んでいたら、「発展・応用」として、けっこう分かりやすくテイラー展開について書かれていた。

* 以下、数式がつづくので、読み飛ばしてもかまいません。

「まとめ」だけ読んでいただけたら嬉しく思います。

　テーラー展開の発想は、「割り勘」の計算と似ている(と思う)。

ある曲線の一部分

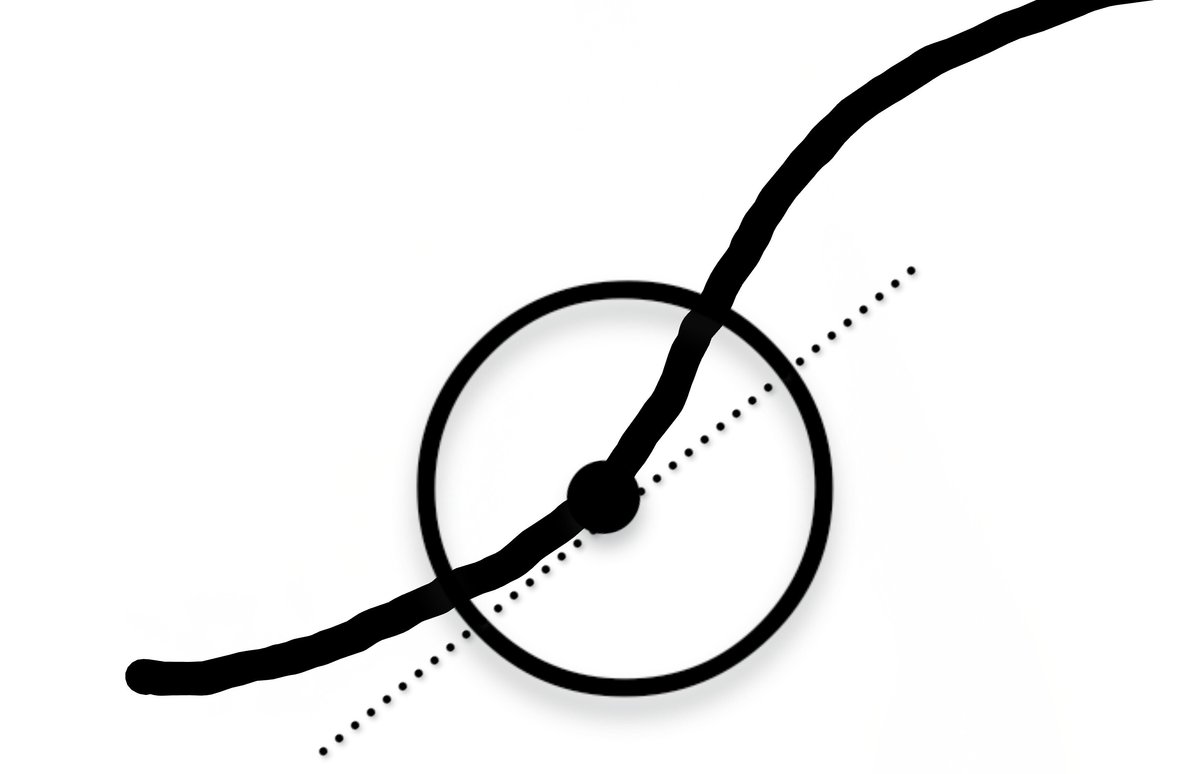
　ある曲線の一部分を顕微鏡🔬で見るように、拡大していくと、最終的には、「・」の近くでは、直線のように見える。つまり、１次関数で近似できる。
　
　「テイラー展開」とは、複雑な関数を簡単な関数に置き換えるようなイメージである。ある関数の接線を求めるのと同じような感じ。

　つぎに、１次関数ではなく、たとえば２次式で、COS x を近似することを考えてみよう。

２次式で近似を考えたから、次は３次式による近似を考えてみる。

　ここに挙げた計算は「あそび」である。
　二つの関数を「……とおいてみる」と書いたが、「＝」は実際には成り立たない。だから「あそび」である。しかし、「あそび」のほうが、厳密な証明より、分かりやすいと思う。
　きちんとした証明は、専門書をご覧ください。

 まとめ

　何度でも微分できる関数の、ある点における接線(１次関数)は、その点の近傍における元の関数の近似式だと考えられる。より精緻な値(近似式)を得たいならば、次元を上げていけばよい。

　先ほど、テーラー展開と「割り勘」とが似ている、と書いた。
　そのこころは。。

　たとえば、３人で飲みに行った。
合計で、

「9681」円だった。

割り勘にすると？
ふつうに３で割ればよいのだが、
桁の大きな部分に注目すると
「9000」を３で割って「3000」円。
残りの「681」円は誰かひとりにお任せしてもいいかもしれない。
　いや、「681」も３人で割ることを考えるなら、桁の大きい「600」円を３で割る。そうすると一人「200」円。
残り「81」円は誰かに任せてもよいだろう。
　いや、ここまで来たら「81」も三等分しようと思えば、
81÷３＝27

きっちり計算すれば、「3227」円だが、どこまで計算するかは、

必要に応じて行えばいいと思う。

「割り勘」と「テーラー展開」の発想は似ている。

　「必要に応じた」数値の扱い方は、普段の生活の中でも、無意識的にみんなおこなっている。
　たとえば、徒歩で学校に通っている子どもに、家から学校までの距離を尋ねれば、「◯キロくらい」とか「◯◯メートルくらい」と答えるだろう。「1234m」のように、下一桁まで正確に答える必要はないだろう。
　車で会社まで通うサラリーマンに、家から会社までの距離を尋ねれば、答えは「◯十キロくらい」「◯◯キロくらい」となるだろう。
　ゆとり教育のころ、円周率は「３」と教えられたという話を聞いたことがあるが、日常生活ならば「３」としても、いいだろう。
　さすがにタイヤのメーカーであれば、「３」ではまずいから、円周率は、
3.141592…と細かい数字まで必要になるに違いない。
　どのくらいの精度まで必要とされるのかは、目的によって変わりうるものだ。