偏微分 | ∂z/∂x, ∂z/∂y

この記事では、微分の意味は考えません。初歩的な公式とその使い方だけを書くことにします。

計算それ自体は、中学１年生でも十分に理解できるレベルです。

(1) 高校生レベルの初歩的な微分

---

(i) y=定数の場合

(ii) y=(xの累乗)の場合

---

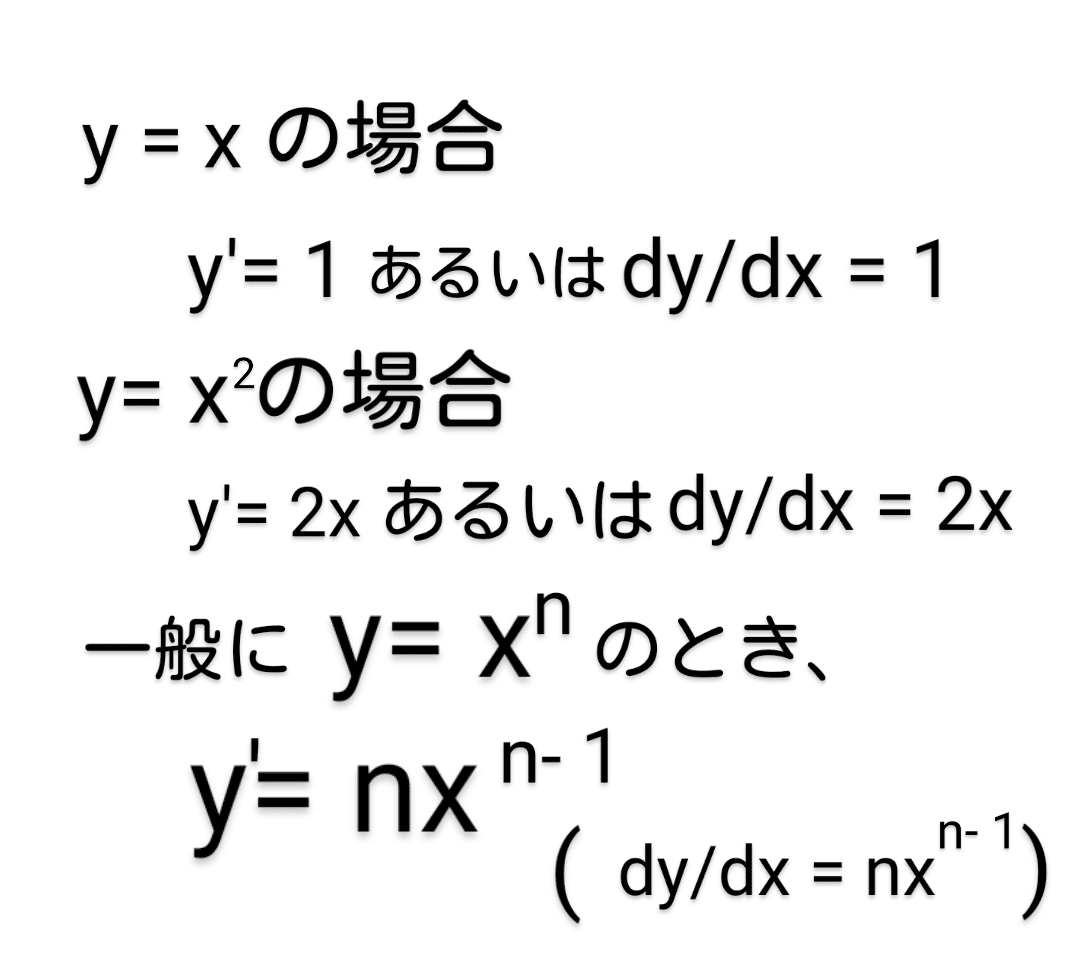
(2) 偏微分 (大学数学初歩レベル)

---

基本的には、(1) の場合とやることは変わりません。ただ文字が増えます。

具体例を２つだけ挙げておけば、とりあえず「やり方」は分かると思います。
たとえ意味は分からなかったとしても😃💕。

高校生までに学ぶ「ふつうの微分」と、大学数学で学ぶ「偏微分」では、表記の仕方が異なります。

決まった読み方は特にありませんが、
y' は「ワイ・ダッシュ」、
dy/dx は「ディーワイ、ディーエックス」、
∂z/∂y は「ラウンドズィー、ラウンドワイ」と読んだりします。

---

---

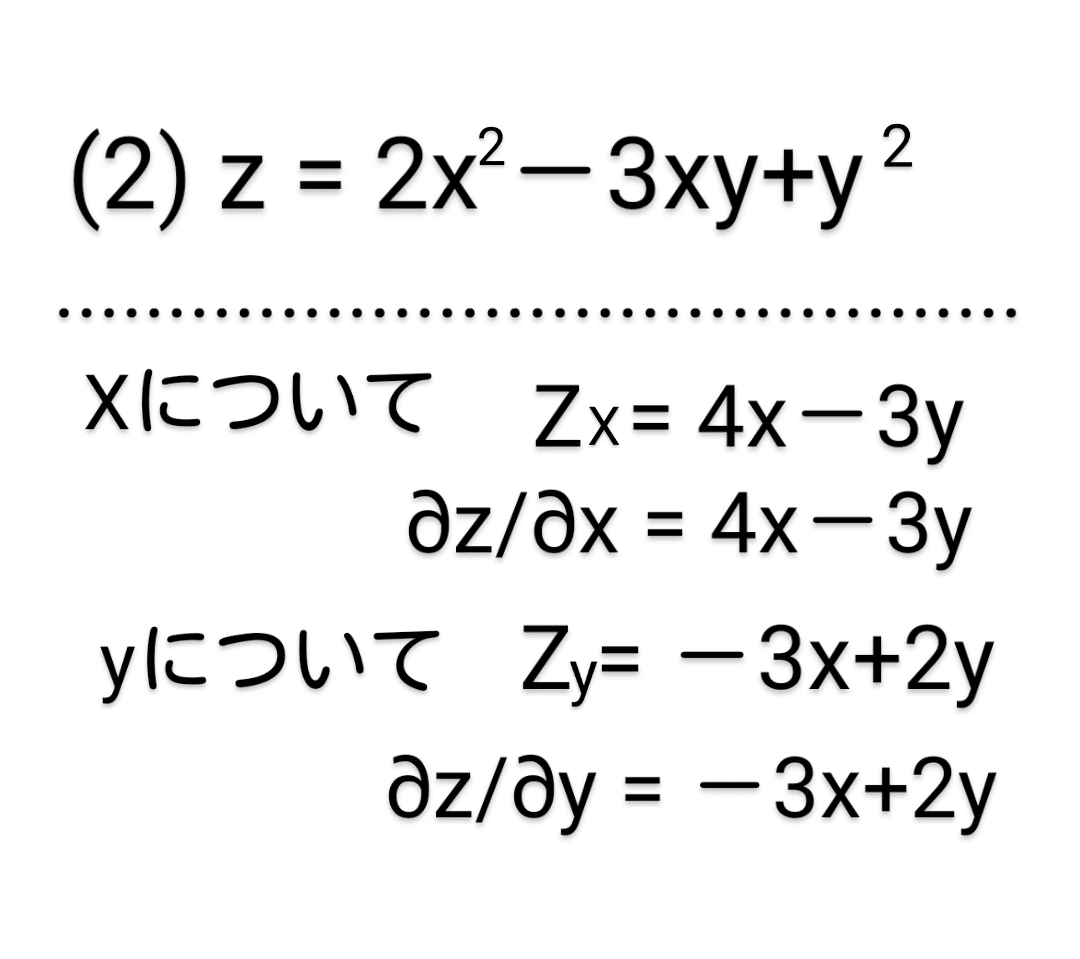
(3) ラグランジュの未定係数法

---

次回の(数学の)記事では、
今回の偏微分の知識を使って、
「ラグランジュの未定係数法」の使い方を説明するつもりです。

気が向いたら… …(^_^ゞ。