【ゲーム分析】【数学の話】太平記の最終問題？をついに解く
この記事の主要な部分は無料です。
はじめに
「太平記システム」の元祖である「SS太平記」は、「ルールはシンプルだが、奥が深い」というSSシリーズのコンセプトそのままの名作ゲームです。
同ゲームの特徴は、『シミュレイター誌32号』の紹介記事（コミック）で、分かりやすく解説されています。
まずは、采配能力。
STR解説委員（以下、編集長）「ゲームでの（足利）尊氏と（新田）義貞をくらべてみましょう。（右側の）数字がちょっと違うでしょ。」
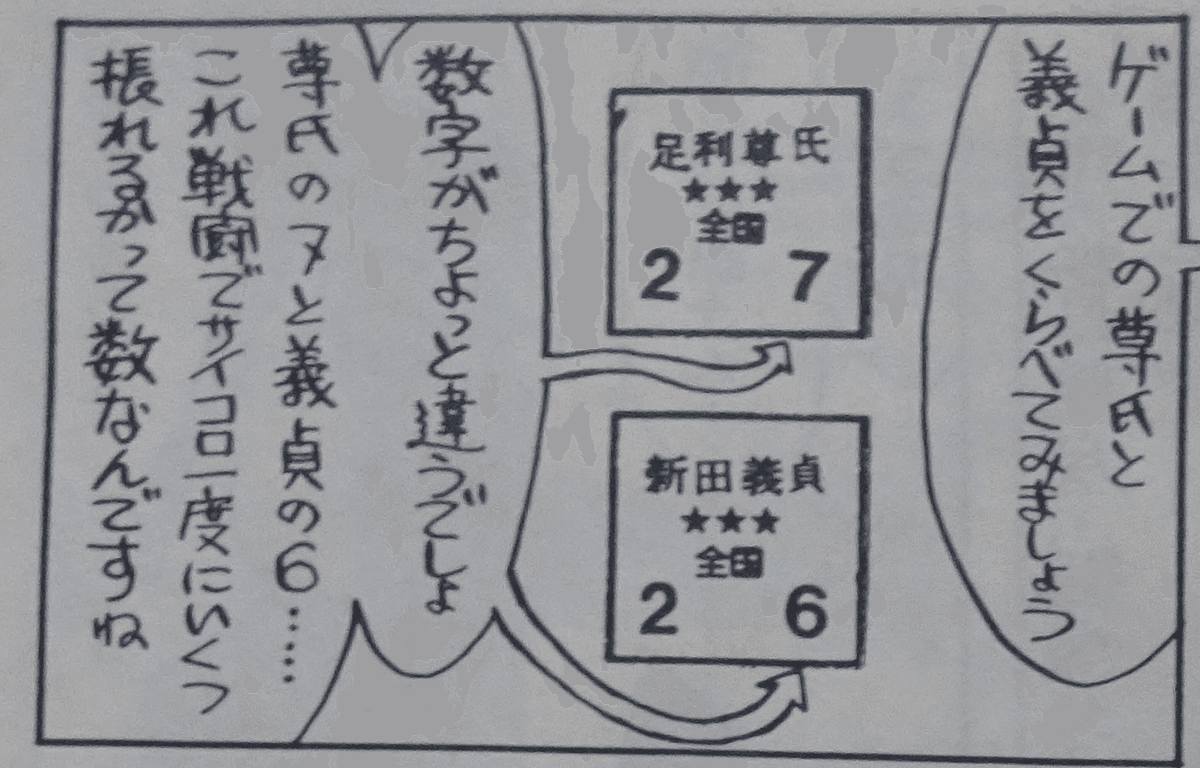
編集長「尊氏の7と義貞の6・・・これ戦闘でサイコロ一度にいくつ振れるかって数なんですね」
聞き手「で、6が出れば敵に一発大当たり、と」
編集長「そうそう。尊氏の方がサイコロ一個分有利なんだな、これが」
次に、合戦能力です。
聞き手「いやー、ソロプレイでゲームやってみたんですけど、北畠顕家強いですねー」
編集長「いやー、そうでしょ。強いんです、この人。ちょっとユニット見て下さい」
編集長「戦闘ではサイコロ6個振れて新田義貞と同じなんだけど、左側の数字に注目して下さい。」
編集長「この3という数字はー、『合戦能力』という数字で、いわゆる戦術的能力ですナ」
編集長「敵の合戦能力と比べて多かったら、多い分だけ振ったサイコロの目にプラスできるんです」
聞き手「すると北畠顕家が尊氏と戦うとー、サイコロ6個振って5・6の目で１ヒット。
対する尊氏はサイコロ7個振って6の目で1ヒット。」
聞き手「どっちが有利なんですか？」
編集長「甲乙つけがたいですねえ。確率計算でもして下さい」
というように、同誌編集長が「北畠顕家と足利尊氏が戦うとどっちが有利かは、確率計算をしないと分からない」と仰るので、僭越ながら筆者が計算して確認してみました。
期待値の計算
実はこの問題は、ゲームに多少慣れている人にとっては大した問題ではないように思えます。
”北畠顕家が尊氏と戦うと、サイコロ6個振って5・6の目で1ヒット。対する尊氏は、サイコロ7個振って6の目で1ヒット。”
という条件であれば、顕家の方がかなり有利であることが、直感で分かるはずなのです。
問0. ヒット数の平均値
例えば、両者ともに最大の（采配能力と同数のサイコロが振れる）条件を仮定すると、1ラウンドで見込めるヒット数の平均値（期待値ともいう）は、それぞれ「2.0（顕家）」と「1.17（尊氏）」になる。
これは、かなりの差だと思います。
この平均値をどうやって計算したのかは、後半の有料部分で説明します。
ヒントとしては、本記事のタイトル画像が何を意味するか、です。
（簡単に「サイコロ1個あたりの期待値をサイコロの個数分合計する」でも出ますが、サイコロではなくくじ引きのように分母が変化するケースでも使える考え方で行きます）
問題の再定義と結論
このように、「顕家の方がかなり有利である」ことは容易に分かることで、専門家が「確率計算をしないと分からない」と言うほどの難問ではないはず。
問1. 両者が10戦力ずつを持つ場合の勝率
まずは、両者が同じ条件であれば結果にどれくらいの差があるか。
「 同数の戦力（例えば10戦力ずつ）を持つ場合、両者の勝率がどれくらいか」を、計算しました。
引き分け：0.28%
顕家の勝ち：92.1%
尊氏の勝ち：7.62%
思った以上に、圧倒的な差でした・・・
なお、この計算をする上で、ゲームとは違う前提がいくつかあるので、書いておきます。
ゲームでは両者とも合戦途中で撤退することができるが、計算ではどちらかの戦力が0になるまで戦う
ゲームでは合戦の前に調略があり、相手の武将が寝返って味方になる可能性があるが、計算では考慮しない
ゲームでは合戦中に味方の武将が損害を受けたときに、降伏して寝返る（敵になる）可能性があるが、計算では考慮しない
問2. 尊氏と顕家が互角に戦える条件
では、尊氏はどのようにして戦えばよいか。
このゲームでは、損害を受けて戦力が采配能力よりも小さくなれば、「戦力分しかサイコロを振れない」という不利な状況になるので、尊氏としては顕家の方が先にその状態になることを期待するしかない。
そのためには、尊氏の方が顕家よりも戦力を多く持っておく必要があります。
そこで次に、「 尊氏が顕家よりどれくらい戦力が多ければ互角と言えるのか」を、検証しました。
ざっくり、尊氏は顕家の1.5倍の戦力を持つ必要があります。
結論は以上で、本記事の有料部分では、これらの具体的な計算方法と計算結果を書いています。
興味がある方は、ぜひ確認してみて下さい！
余談
「SS太平記」の北畠顕家と足利尊氏。ここまで数字上の大差がありながら、ゲーム専門誌の編集長が「甲乙つけがたい」と言うのは、どういうことなのか。
尊氏が優ってるのは、顕家よりもサイコロを振る数が1個多いこと。
多い分の1個が毎回6じゃないと互角にはならないのだが、逆に言えば、その1個が毎回6であれば互角、とも言える。
当時、恐るべきサイコロ運を誇るH氏・O氏というゲームプレーヤーがいました。（「怪傑ピンゾロ」「超人ロク」と呼ばれていたとか、いないとか・・・）
彼らなら、本当に毎回6を出してもおかしくない（？）
そういう伝説的なゲーマーたちを日頃目にしていたら、確率などただの数字に過ぎない、と思ってしまうのも無理はありません！（？）
ここから先は
¥ 300
貴重なお時間を使ってお読みいただき、ありがとうございました。有意義な時間と感じて頂けたら嬉しいです。また別の記事を用意してお待ちしたいと思います。