見出し画像

[大学]院卒が量子論,量子力学,量子コンピュータの本をオススメするよ。準備(数学&解析力学)編(2022年版)

san. | いい日たびたび

※ この記事は書名を著者さんの名前で記載します。その際に敬称を省かせていただきます。また、わたしは挙げた本をほぼ所持していますが、それら全てを隅々まで学んでいません。わたしの自身の経験から、できる限り苦労しないで、凡人が量子力学を学ぶ方法を提案する記事です。


イントロ

さて、続きです。
この記事では準備の本をピックアップします。
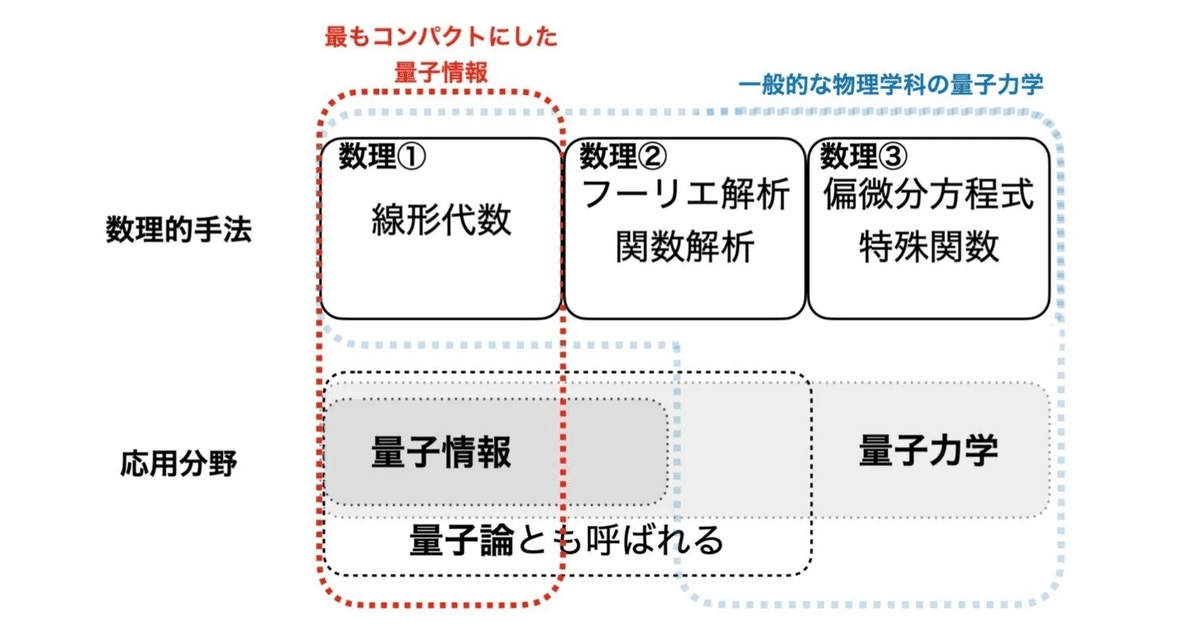
対象は「もっともコンパクトにした量子情報」~「一般的な物理学科の量子力学」の全般です。

準備する分野は、こちら。

  • 数学

    • 線形代数

    • 微積分

    • 複素関数(複素解析) <- 量子情報であれば不要, 同時進行で可

    • 関数解析 <- 必須ではない

    • 偏微分方程式 <- 量子情報であれば不要

    • フーリエ解析 <- 量子情報であれば必須ではない

  • 解析力学

この記事ではこれらを全般的に書きません。というか、関連記事の準備が整っておらず、今後追記していきます。また、各分野へ深入りしないことを原則としています。各分野を完全に修めるのは、量子力学を学び終えた後にしてほしいからです。先に物理を進めましょう。

ところで、はじめて量子力学を触れる方から初期量子論は?と尋ねられることがあります。聞いた本人が初期量子論と自覚していないかもしれませんが、量子力学が生まれる前夜の知識についてです。初期量子論は不要です。なぜなら、初期量子論は量子力学パラダイムの前にあたるからです。量子力学の理論は、初期量子論以後に整備されていきました。量子力学の本のはじめに書いている程度の初期量子論で十分です。読み飛ばしてもいいです。初期量子論はどちらかというと量子統計力学です。学びを進めるとまた返ってきます。

線形代数

必須です。記事をご覧ください。

とはいっても、量子力学の1周目であれば

が終了した段階でも大丈夫です。必要になる線形代数の性質は、量子力学の本で解説されるからです。笠原「線型代数と固有値問題」まで進んでいれば、量子力学の数理(関数解析)を学ぶ基礎が出来上がります。

微積分

1変数の微積分、微分方程式、偏微分・重積分が計算できるレベルが必要です。イプシロンデルタ論法は出来たほうがいいかもしれない程度です。

こちらの学習院大学 田崎清明先生の数学のテキストを消化していれば、十分です。

記事を書きました。量子力学1周目の段階では、この記事でのその1:基礎編で大丈夫です。量子力学がある程度進んでから、その2:解析学手前などに進んでください。


複素関数(複素解析)

こちらに書きました。この記事での入門編を参考ください。量子力学と同時進行でも可です。

解析力学

量子情報の方は不要です。ただし、量子情報でも解析力学を用いる場合があります。量子情報であっても「一般的な物理学科の量子力学」のアプローチを取られる可能性があるからです。有名なNielsen & Chuangであれば解析力学を使いません。とはいっても、解析力学じたいが量子力学と同様に面白く(後述)、知っていても損ではありません。小野寺嘉孝「物理のための応用数学」(裳華房,1988)での変分法だけでも知っておくとオトクかもしれません。

量子力学で展開される理論は、正準理論が土台になっています。いいかえると、正準理論を量子化すること(正準量子化)は、量子力学への手続きを行うことにあたります。このため、量子力学を学ぶには、正準理論の基礎となる解析力学が必要になります。量子化には、実際はいくつかあります(Wikipedia)。Wikipediaには多く書かれていますが、通常、使われる量子化は正準量子化で、そしてファインマンによる経路積分量子化があります。経路積分アドバンスドな方法であり、量子力学の基礎で学ぶ間は使用しません。

有名ですよね。量子力学で必要になる解析力学だけをまとめた本です。コンパクトとはいえ、解析力学がもつ独自の理論体系を丁寧に説明されており、解析力学入門としても使える良書です。

解析力学は、理論物理学での美味しいところ(面白い)なので、上記の本を起点として、どっぷり解析力学に浸かるのもおすすめです。

など現代的な良書もありますし、

関数解析

「一般的な物理学科の量子力学」向けの話題です。ぶっちゃけ、知らなくても、量子力学を問題なく進められます。

この本を関数解析に挙げるのは、数学屋さんに文句いわれそう。下記をお読みいただければと思います。

量子力学は、数学的には「ヒルベルト空間上の演算」といえます。これは、線形代数が有限次元での行列とベクトルの演算であったことに対応して、それを無限次元に拡張した概念にあたります。ベクトルは関数に、行列は線形作用素、内積は積分(重積分)に、そしてベクトル空間はヒルベルト空間に、と変わります。ヒルベルト空間とはいえ、線形代数で成立することは、同じく成立します。本当なの? を探るのが関数解析学です。ヒルベルト空間論は関数解析学の一部です。関数解析学にいきなりすすむのではなく、笠原「線型代数と固有値問題」や志賀浩二「固有値問題30講(数学30講シリーズ)」を取り組みましょう。

という名著があります。ご存知ですよね。測度論を未修の方はコチラをオススメします。

※ 書き漏れが多すぎるので記事を改めて書く予定です。

偏微分方程式

「一般的な物理学科の量子力学」向けの話題です。
「一般的な物理学科の量子力学」の場合、偏微分方程式ができないと早々にコケます。難しい偏微分方程式本を読まなくてもいいので、下記だけやりましょう。偏微分方程式にハマる(どっぷり浸かる)と、なかなか戻ってこれないんです。

そっか、「解析学概論」には偏微分方程式は載ってなかったよね。

特殊関数

そして、特殊関数が出てきます。いくつか特殊関数の本を持っていますけど、使いやすい本はコレなんですよね。「詳解応用物理数学演習」は量子力学を学んでいる最中だとイミフでしょうし。

繰り返しますが、この分野は深入り禁止ですよ。

とかね。魅力的な本が多すぎるのです。

フーリエ解析

「一般的な物理学科の量子力学」向けの話題です。
そもそも量子力学を複素関数をやらずに学ぶのは無謀なんです。

複素関数ありのフーリエ解析を、量子力学と同時進行で取り組むのをオススメします。コチラに書きました。この記事の入門篇を参照ください。

こちらの複素解析と応用解析の章をやりましょう。

複素関数ありのフーリエ解析であれば、「フーリエ解析(理工系の基礎数学 6)」(1997)も持っていると、場の量子論で使えます。端的にいえばグリーン関数なんですが。フーリエ解析から緩やかにグリーン関数へ導入している本をコレしか知りません。こっち向きのフーリエ解析本ってほとんどありません(知りません)。同程度であれば小野寺嘉孝「物理のための応用数学」(裳華房,1988)、また今村勤「物理とグリーン関数」(岩波書店,2016)だと少しレベルが上がります。もちろん、ここのお話は量子力学1周目では不要です。

全部盛り

全部盛り、実はあります。ただし、微積を除きます。こちらの本は、量子力学を学ぶと並行して、随時進める内容です。量子力学1周目段階で修了していなくても構いません。

佐々木隆「物理数学」(培風館,1996)の目次を添付します。(不正利用しないでくださいね)。この本は、数学だけでなく解析力学も含まれている、まさに「量子力学で必要となる基礎知識」本です。

培風館さん、ぜひ復刊してください。安く手に入れるチャンスがある方は買っておきましょう。
類書を思い出しました。
小野寺嘉孝先生による教科書と演習書があります。アマゾンの試し読みが混乱気味ですね。出版社HPの目次ページのリンクを付けておきます。佐々木隆「物理数学」(培風館,1996)と比較すると、小野寺 本では、解析力学が汎関数(変分法)に、また特殊関数、グリーン関数が多めになります。小野寺 本は統計数理、人工知能の数理としても使える内容です。

そして、

こちらは理論物理学全般、古典物理学を含む、量子力学のための数学本です。アマゾンレビューに詳細に書いてくれているのでそちらを参照ください。

全部盛りということであれば前述のアルフケン(の原書 Arfken&Weber, Mathematical Methods for Physicists)も相当します。

最後に

ぱっと思い出せる本を列挙しました。他に気付いた本がありましたら、都度追加します。

いいなと思ったら応援しよう！

この記事が参加している募集

#数学がすき

3,197件