
数学(2022/6/15_2):キューネン本2冊についての記事_9.ZFC集合論の公理のリスト_7(中間生成物:基数としての自然数)
(2022/6/15 19:00頃)配置移動済。また「特に順序数における基数としての後続順序数」等の項目追加
(2022/6/18 17:30頃)「順序数の差」と「前者順序数」の項目追加
(2022/6/19 6:30頃)「フォン・ノイマンの割り当て」において「始順序数」の記述を追記
(2022/10/19 20:00頃)「順序数全体の真クラス上の超限再帰」において「整列可能集合における超限帰納法」の記述を追加
1.ZFC集合論の公理のリストから中間生成物を構成する(続き)
今回は「基数としての自然数」の話をやります。
順序数としての自然数と基数としての自然数が揃うので、これで実質「自然数」そのものの話をしたのと同じ意味になります。
単純に例示のために、あらかじめ先に書きますが、「基数」とは何かというと、「「個数」というものを、より一般的に使えるようにしたもの」です。
分かりやすさのためにいうと、我々の考える個数は、ものや、集合の要素を数え上げる時に使われるものです。実際そういう使われ方をしていますね。
そして、後述しますが、これは実際には順序数としての自然数と対応するものです。
ということで、「基数としての自然数」、「有限基数」または「個数」と呼ばれるものの話を、後でまとめてします。
***
実は、基数の話は、「特に順序数における基数」について語る方が、「集合一般における基数」に比べて楽です。
基数が簡単に出せる集合と、そうでない集合があり、順序数は簡単なのです。
これはなぜそうなるかというと、必要とされるキーワードと、必要とされるZFC集合論における公理が、少なくても済むからです。
なので、こちらを先にやってしまいましょう。
そして、これを使えば、「基数としての自然数、有限基数とか個数とか呼ばれるもの」にたどり着けます。
***
さしあたり、
濃度
特に順序数における濃度
特に順序数における基数
基数としての自然数、有限基数とか個数とか呼ばれるもの
という順に説明していきます。
1_1.濃度
1_1_1.全射・単射・全単射と、集合の「ある種の大きさ」の発想
前触れた「(広義の)函数」のパターン、「全射」「単射」「全単射」の話を、もう一度します。
***
「全射」では「始域が終域より大きいある種の大きさを持つ」と見立てられる。
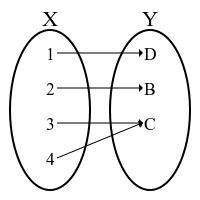
「単射」では「終域が始域より大きいある種の大きさを持つ」と見立てられる。
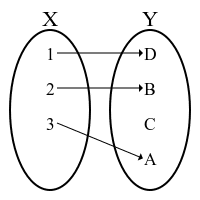
「全単射」では「始域と終域が同等のある種の大きさを持つ」と見立てられる。

このように、全射・単射・全単射と、集合の「ある種の大きさ」には、何らかの関係がありそうなのでした。
1_1_2.この「ある種の大きさ」を、たいていの量がそうであるように、実際には数で扱えたりするのではないか
この手の「ある種の大きさ」は「ある種の量」なのです。
そうなると、たいていの量がそうであるように、実際には数で扱えたりするのではないか。
少なくとも、まずは一番初歩的な数、順序数で。
1_1_3.大きさを測りたい「集合」を「整列可能集合」に見立てる
さて、なんとここで、順序数の少し手前の順序関係、
「より大きい、より小さいというタイプの(狭義の)」
「一直線上の順序関係(全順序関係)であり」
「常に一里塚があるもの(整礎的関係)」
すなわち「整列順序」が出てきます。
ある集合を使って、整列順序を設定した場合、それの一側面としての集合は「整列可能集合」と呼ばれるのでした。
では仮に、大きさを測りたい集合について、そのようにやってみましょう。
1_1_4.バラツキのある目盛りとしての整列順序、バラツキのない特別な目盛りとしての順序数
「やってみましょう、とは言うものの、なぜそのようなことをすることになるのか? 何のメリットがあるのか?」
前も書きましたが、整列順序のパターン分けのための「特別な整列順序」における「整列可能集合」が、実は「順序数」そのものと一致するのでした。
整列順序の一里塚だけでは
「そういうものがあるのは分かった。
それがどうしたのか?
ある種の大きさを測るのに役立つのか?
一里塚と一里塚の間に何か要素があってもなくてもいいのだろう。
もし何もなければ、確かにその一里塚は目盛りとして役立つだろう。
だが、何かあったら、それは目盛りとしては実用に耐えない、滅茶苦茶なものになるではないか。
一里塚を持ついくつかのそうした順序関係があった時に、それらをそれぞれ目盛りとして使ったら、ある目盛りと別の目盛りで違うバラバラの値が出るぞ。
それでは話にならないではないか」
と突っ込まれても仕方ありません。
***
が、
「ですので、一里塚と一里塚の間に何もない場合のみに、話を限りましょう。
この目盛りなら常にバラツキの全くない同じ値になりますね」
という対処はできます。
そしてこれは実は、「特別な整列順序」の「整列可能集合」、「順序数」を使っているのと同じ意味になります。
1_1_5.こうして「集合のある種の大きさを測る手段」が手に入る
ここからが本題になります。平たく言うと、
「集合」をあらかじめ「整列可能集合」として見立てて
これと「特別な整列可能集合」である「順序数」を
「完全に対応している」「全単射」にしておく
ことで、実はこれが「ある集合のある種の大きさを測る」操作と同じ意味になります。
***
これにより、集合である「始域」と「終域」をいったん順序数の世界に翻訳して、比較することも可能になるのです。
その結果、ちゃんと
「全射」では「始域が終域より大きいある種の大きさを持つ」
「単射」では「終域が始域より大きいある種の大きさを持つ」
「全単射」では「始域と終域が同等のある種の大きさを持つ」
ことが言えるようになります。
1_1_6.では実際にこれで集合のある種の大きさを測ればよいわけだ
すると、逆転の発想で、こう考えることもできます。
「異なる集合の大きさを測るなら、それぞれを(広義の)函数の始域と終域と見立てて、それらの間で「対応する順序数」の比較をすればよい。
特に、全射か単射か全単射であることが分かっている場合、上の三つの大小同等が言えるという、単純明快なメリットがある」
1_1_7.フォン・ノイマンの割り当て
さて、順序数はバラツキのない、無駄のない目盛りとして使えるのでした。だから、ここで必要最小限の目盛りを使うことができたら、ブレの全くない測量になり、運用上完全に無駄をなくせます。つまり、
「ある集合の大きさを測るのに、一番無駄のない必要最小限の目盛りで測りたい。
つまりは、最小の順序数を用意したい」
というニーズが出てきます。
さて、『形式言語』の記事で、始順序数の話をしたのでした。
自然数そのものか、"omega-n" であるようなもののことです。
上でいう最小の順序数に、実はこの始順序数を使うことになります。
この手法は『フォン・ノイマンの割り当て』と呼ばれます。数学者フォン・ノイマンが考案したからです。
1_1_8.「正確に測りきられた、集合の「ある種の大きさ」を表す数」、「濃度」
『フォン・ノイマンの割り当て』の結果、
「ある集合のある種の大きさを正確に測りきれる完全な目盛り」
が得られます。
これである種の大きさを正確に測りきることができますし、これをある種の大きさそのものを表すものとして、事実上同一視できます。
この、「正確に測りきられた、集合の「ある種の大きさ」を表す数」が、この節の題でもある、「濃度」というものです。
ある集合 α の濃度は、 |α| と表記されます。
1_2.特に順序数における濃度
1_2_1.順序数においては濃度を測るのは極めてたやすい
さて、
「ある集合を整列可能集合に見立ててから順序数の世界で比較可能にする」
という手法ですが、この手順を非常に省略できる、ある種の集合が存在します。
何か。
外ならぬ「順序数」です。
これだと「順序数を順序数の世界で比較可能にする」ので、それはもう直ちに大きさが分かるというものです。
(だいぶ複雑怪奇な作り方ですが、「順序数」というものは、実態としては奇妙な形のタマネギめいて重なり合った、「集合」の一種なのでした)
1_3.特に順序数における基数
1_3_1.順序数における濃度はいろいろな値が取れるが、必ずその順序数以下になる
実際に順序数における濃度をとってみましょう。
今までの話だと、順序数は、たとえば5を例にとると、{4, {4}}と表せたり、{0, 1, 2, 3, 4}と表せたりするのでした。この場合、前者の濃度は2であり、後者の濃度は同じ5ですね(見ての通りです。数えてみましょう)。
このように、ある順序数の濃度はいろいろな値が取れるのですが、必ずその順序数以下になります。
(順序数はタマネギみたいな構造の集合になっており、構造の都合上、それより多くの要素を持てません。)
1_3_2.順序数における濃度の中でも、「ある順序数そのものと同じ値の、ある順序数の濃度」は、一番正確な濃度として特別扱いしたい
特に、ある順序数とある順序数の濃度が同じだった場合、
「この濃度、またそれと同じ値であるこの順序数そのものが、ある順序数の要素の個数を、一番正確に表している」
と思いたくなります。
具体的には、「5の濃度で、特に5こそが、一番正確な5の濃度である」と言いたくなります。
1_3_3.特に順序数における基数(再掲)
ということで、この、
「ある順序数とある順序数の濃度が等しい場合、その順序数」
を、特別に
「特に順序数における基数」
と呼ぶことにします。
これが、
「その順序数の濃度として一番正確な値とみなせるもの」
です。
1_4.特に順序数における基数としての後続順序数
1_4_1.順序数の差
さて、最終的には『基数としての自然数』、"aleph-0" が欲しい訳です。
単純に『特に順序数における基数』の、特に 0 と後続順序数に限った場合を考えればよさそうに思います。
0 は簡単です。
「『特に順序数における基数』としての 0 とは、順序数 0 のことである」
これで終わりです。
しかし、実は、『特に順序数における基数』としての後続順序数を考えようとすると、いくつか下準備が要ります。
そして、これからするのは、その話です。
***
まずは、順序数の減法(引き算)、順序数の差(引いた後の値)の話をします。
とはいえこれは、『形式言語』の記事で述べた、順序数の加法(足し算)、順序数の和(足された後の値)を応用すれば簡単です。
「足される側の値」と「足す側の値」と「足された後の値」を考えましょう。
例えば、α + β = γ のとき、「足される側の値」は α、「足す側の値」は β、「足された後の値」は γ であるとします。
順序数の減法のとき、γ - β = α として、「引かれる側の値」は γ、「引く側の値」は β、「引かれた後の値」は α であるとすれば、これは上の順序数の加法と対応します。
(なお、この時点では、まだ整数の構成をしていないので、引かれる側の順序数は、引く側の順序数以上でなければなりません。気を付けるべきところはそこだけです。)
1_4_2.前者順序数
まずは、後者順序数にある意味で対応する順序数、前者順序数の話をします。
とはいえこれは簡単です。
後続順序数 S(α) を考えます。これは順序数の和 α + 1 と等しいのでした。
このとき、順序数の差 S(α) - 1 = α が、すなわち前者順序数です。
見ての通り、後続順序数と逆の発想ですね。
1_4_3.整列可能集合における超限帰納法
さて、通常帰納法のところで少し触れた、超限帰納法の話をします。
通常帰納法はある意味で有限である自然数を扱い、無限である自然数全体の集合について論じるテクニックでした。
超限帰納法はこれと違い、扱うのはもっと緩い、整列可能集合です。
***
では、超限帰納法とは何か?
「整列可能集合の全ての要素について、ある命題が成り立つ」
こととします。
これらは整列可能集合の要素なので、最小要素があります。
さて、もし
「最小要素においてその命題が成り立たなかった」
としたら、
「整列可能集合の全ての要素について、ある命題が成り立つ」
ということは成り立たなくなります。
つまり、最小要素においてその命題が成り立たなかった場合を仮定して、それが矛盾したら、背理法に鑑みて、
「最小要素においてその命題は成り立つ」
と言い切れます。こうなると、
「整列可能集合の全ての要素について、ある命題が成り立つ」
ことを妨げるものは何もなくなりますし、これについても確かだと言えるようになります。
(詳しい証明は、テクニカルで煩雑な話になるので、説明しません。)
1_4_3.順序数全体の真クラス上の超限再帰
さて、この記事全体においては、『超限再帰』と呼ばれるものを、2回使います。
今回説明する『順序数全体の真クラス上の超限再帰』と、
基礎公理のバリエーションとしての、『万有クラス上の超限再帰』と、
です。
今回使うのは前者です。
(後者は基礎公理の時に説明しますので、それまでお待ちください。)
超限再帰の基本的な考え方は、
「ある函数があるとする。
それを使って、同じ構造の函数を作る。
これを反復する」
という仕組みです。
そういえば、初めの頃に出てきた、置換公理図式や内包公理図式は、あらかじめ出力先の数学的対象を使ってはならないのでした。
しかし、ある程度練り上がった数学的対象を、適正な作法の上で、反復に使うことは、実は問題なくできます。
その作法の話を、これからします。
***
一般に、超限再帰は、2つの部分に分かれます。
1.「「全てのxについて、yがただ一つ存在する」
という条件に従う、なんらかの2変数論理式を考える。
この場合、x になんらかの函数めいたものを適用して、像めいたものとしての y を確定させた、という意味合いになる。
だから、y=F(x) と考えても良い」
2.「こうした論理式を2つ用意し、F と G とする。
x を使ってある種の加工をしたもの、f(x) による、F の制限函数 F|f(x) を考えてみる。
(この論理式は実際には集合として機能するため、この制限函数は問題なく制限函数として機能します。
置換公理図式は、この手の加工したものの集まりを、結果的には集合として認めるのでした。)
すべての x で F(x)=G(F|f(x)) となるようにできる。
この結果、F と G を同じ構造の函数として同一視することが可能になる。
処理を止める条件を設けていないので、同じ構造の函数を果てしなく作ることができる」
これが
「ある函数があるとする。
それを使って、同じ構造の函数を作る。
これを反復する」
という仕組みの定義です。
順序数全体の真クラス上の超限再帰の場合は、f(x) として、具体的には順序数全体の真クラスに所属すると見立てられた、順序数 x そのものを使います。
こうすると、上の論理式は、ちゃんと期待通りに動作するのです。
(万有クラス上の超限再帰の場合は、別のものを使いますが、それはまた後の記事で説明します。)
***
さて、不思議な話をしますが、超限再帰には形式言語が効いてきます。
より正確には、函数記号で拡大された形式言語が、です。
函数記号として何が想定されているかというと、もちろん F と G です。
中に何らかの値を入れることで、何らかの別の値が手に入るのだから、これは函数記号の性質を満たしています。
「函数記号で拡大された形式言語の例として、F と G を入れた形式言語を考えると、F と G を使った万有クラス上の超限再帰が、ZFC集合論で問題なく扱える」
ということです。こんな応用があるんですね。
***
また、超限再帰には前者順序数と整列可能集合における超限帰納法も使います。
(こちらも、説明がそうとう煩雑になるので、説明を致しません。)
1_4_4.超限再帰的函数と呼びうるもの
超限再帰が成り立つ場合、この函数 F を、個人的に『超限再帰的函数』と呼ぶことにします。
(本当は別の呼び方があるはずですが、どうも調べてもピンと来ません。どなたか教えて下さると大変助かります。)
***
これは大変便利な函数で、繰り返しの函数使用を正当化します。
そのため、実は見慣れたものに使われます。
具体的には、
後者函数の繰り返しで自然数の和を、
自然数の和の繰り返しで自然数の積を、
自然数の積の繰り返しで自然数の冪を、
定義することができます。
1+1+1+1 = 1×4 = 4
ですし、
4×4×4 = 4^3 = 64
なのです。
実は、こうしてみれば、自然数のいくつかの演算とは、超限再帰的函数で構成可能なのです。
***
(以下はおまけになります。意味の分かる人以外は飛ばして下さって結構です。)
(順序数の和や積や冪は、自然数の和や積や冪といくつかの違いはあるものの、たいへんよく似ております。
実はここで例として順序数の和や積や冪を用いても、本質的には説明に支障はなかったのです。
だから本当はそうしたかったのですが、我々が馴染んでいるのは自然数の和や積や冪の方なので、分かりやすさ優先で行きました。)
***
そして、別の応用があります。
超限再帰的函数により、以下の主張が正当化されます。
「ある集合とその部分集合があり、集合から部分集合に単射があるとき、集合と部分集合は全単射すなわち同濃度である」
単射のことを思い出すと、終域は始域以上のある種の大きさを持つはずでした。
一方、始域が集合で、終域が部分集合であるならば、部分集合は元々の集合以下のある種の大きさを持つので、
「濃度として以上かつ以下なので同濃度であること」
が言えそうに思えます。
実際には、まだ
「濃度として以上かつ以下ならば同濃度であること」
の証明はなされておらず、むしろこれを証明するために
「集合から部分集合に単射があるならば同濃度であること」
の話をすることになります。
そして、
「集合から部分集合に単射があるならば同濃度であること」
の話をするために、実は超限再帰的函数を使うことになります。
(証明は面倒なのでしませんが、実際に成り立ちます。)
「集合から部分集合に単射があるならば同濃度であること」
により、結果的に
「ある順序数における濃度が、ある順序数と同濃度である」
という事態が正当化されます。
1_4_5.特に順序数における基数でない順序数
さて、上の方で『特に順序数における基数』の話をしました。
「ある順序数とある順序数の濃度が等しい場合、その順序数」
が、特に順序数における基数に他ならないのでした。
逆に言えば、基数でない順序数というものの定義もできます。
「ある順序数未満の順序数と、ある順序数が同濃度であれば、ある順序数は特に順序数における基数ではない」
ということになります。
ここで
「ある順序数における濃度が、ある順序数と同濃度である」
という事態が効いてきます。
(ある順序数を超過する順序数については考えません。
さかのぼった果てに、0 でけりがつく分、未満で考えた方が楽です。)
1_4_6.特に順序数における基数としての後続順序数
いよいよ本題に近付いてきました。
ここでの暫定目標は、「基数としての自然数」、『有限基数』または『個数』と呼ばれるものでした。
粗々と考えると、自然数は0と後続順序数で作れるので、
「0も後続順序数も基数であった」
ならば、有限基数を構成できそうに見えます。
もっと言うと、
「0は特に順序数における基数である」
ということにして、
「後続順序数も順序数における基数である」
ことが保証されれば、作られた自然数は全て基数です。
さて、
「後続順序数が特に順序数における基数であること」
を証明するか、古典論理、背理法を使っての、
「後続順序数が特に順序数における基数でない順序数であったとして、矛盾が生じること」
が証明されれば、上の議論が全て正当化されます。
実際の路線としては下を使います。
つまり、基数でない順序数としての後続順序数の矛盾によって、背理法を使えば、要するに
「後続順序数が特に順序数における基数であること」
も言えたのと同じことになるのでした。
(詳しくは煩雑になるので説明しません。)
1_5.基数としての自然数、有限基数または個数と呼ばれるもの
特に順序数における基数のうち、順序数を自然数のみに限った場合のもの、つまり0と後続順序数の場合を考えました。
これらを一体のものとして扱うと、なんとこれが世間的に言われる個数そのものになります。
より細かく言うと、数学的には『有限基数』と呼ばれるものです。
こうやって構成されるのですね。
***
順序数としての自然数と、基数としての自然数を合わせて考えると、我々にもお馴染みの『自然数』が手に入ります。
実質には、個数と自然数の話を同一視しても問題ありません。
ようやくここまで辿り着きました。
2.次回予告
『基数としての自然数』が手に入ったので、自然数の話はおしまいです。
自然数が欲しいだけであれば、これでこの記事は終了です。
お疲れさまでした。
***
しかし、中にはこういう方もいらっしゃるかもしれません。
「これまでに順序数としての自然数全体の集合の話をしたはずだ。
では、基数としての自然数全体の集合の話があるはずだ。
単純な個数を超えた、基数としての自然数全体の集合とは、どのようなものなのか?」
「ZFC集合論の公理はこれで終わりなのか。
以前の羅列によると、『基礎公理』と『選択公理』の2つの話がまだではないのか?」
***
ということで、今から『基数としての自然数全体の集合』、"aleph-0" と呼ばれるものを作るのです。
実は、必要となる概念が大変多くなるため、かなり長い道のりにもなります。
このため記事をいくつかに分割します。ご了承ください。
それでは、次回以降も、ご期待下さい。
(続く)
いいなと思ったら応援しよう!

