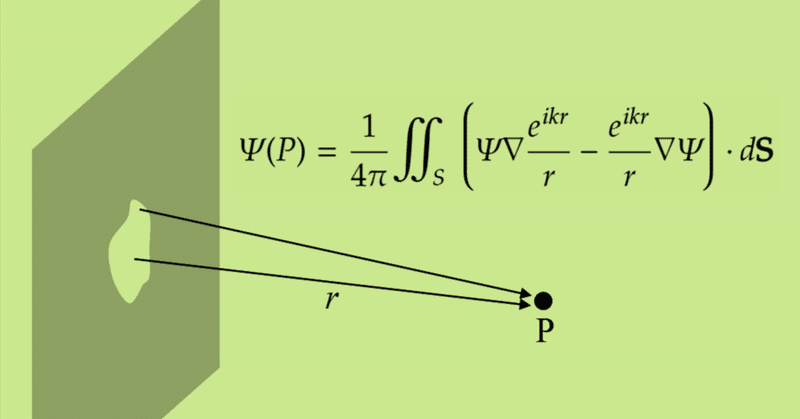ちょっと上級の物理学（たまに数学）｜hydraenids

2024年10月27日 23:56

コハモグリ類の幼虫はいかにして葉を折り曲げるか？―リーフマイナーの蛹室形成の物理―

葉の折り曲げの謎　ミカンコハモグリPhyllocnistis citrellaという蛾がいる。開張（翅を広げたときの幅）が5 mmほどしかない大変小さな蛾である。

上記の写真だと分かりにくいが、翅に金属光沢があり、銀細工のような美しさがある。美しいとは言っても、本種はミカン科樹木の害虫で、ミカン農家にはミカンハモグリガの通称でよく知られている。本種は幼虫も当然ながら微小で、終齢でも体長3 mmほ

もっとみる

hydraenids

2024年9月14日 09:05

無限井戸型ポテンシャルに波束を置くとどうなるか？―古典論と量子論のシームレスなつながり―

はじめに　量子力学の初学者が「何をやってるのか分からん」状態になる最大の原因の1つに、古典力学とのつながりがなかなか見えないことがあると思う。大学の学部の量子力学の授業だと、ポテンシャル束縛系の問題として、調和振動子と水素原子の厳密解を求めるのは定番のネタだが、そこで習うのは通常、時間に依存しないエネルギー固有状態の関数形のみである。ポテンシャルに束縛された粒子が古典論的に動く描像は、一体どこへ

もっとみる

hydraenids

2024年7月30日 17:56

スピン測定に関わるパラドックス的問題―シュテルン=ゲルラッハ実験考—

はじめに　物理学で博士号を取った私だが、量子力学というのは、つくづく、学ぶための敷居が高いと思う。古典力学と比較して物理的な概念や考え方がガラリと変わるため、慣れるまでに時間を要するのだ。自慢ではないが、私の場合、授業で習ったことがいろいろ腑に落ちたのは、大学院の博士課程に入った頃だった（バリバリの理論系志望でない限り、こんなものじゃないだろうか？）。物理学科の学部時代、3年次から始まった本格的

もっとみる

hydraenids

2024年6月24日 21:12

ベルの不等式の直観的理解—隠れた変数のモデルを大真面目に考えるー

はじめに　2022年のノーベル物理学賞は、ベルの不等式の破れを実証し、量子情報科学を開拓した業績で、アスペ、クラウザー、ツァイリンガーの3氏が受賞したのは記憶に新しい。20年前の大学院時代、私の博士論文の研究テーマが「陽子対のスピン相関の測定によるベルの不等式の検証」だったので、この分野の実験家からノーベル賞が出たのは感慨深いものがあった。ベルの不等式は、2つの系が量子論的にもつれた状態にあるとき

もっとみる

hydraenids

2024年6月1日 14:37

連結器の配送問題—大正時代の国鉄の大事業—

今回は小ネタ。大学の学部時代、在籍していた物理学科で「アルゴリズムとデータ構造」という選択科目の授業があった。当時、この手のコンピュータ関連の話には全く興味がなく、単位を揃えるために仕方なく受講していただけのため、どんな内容だったのかほとんど記憶に残っていない。その授業で、日立グループの現役の研究者の方が1回だけ講義に来たことがあった。普段接点のない企業研究者の話が聞けたので、少しだけ新鮮味があっ

もっとみる

hydraenids

2024年4月22日 01:13

ターンテーブル上を転がる球の不思議な運動

はじめに「楽しめる物理問題200選」という、物理の問題集がある。

大学の学部生向けの問題集で、題材は主に古典物理学の範囲だが、なかなか興味深い問題が集められているのだ。一見難解に見えても、ある気付きを得ると簡単に解けるような「補助線一発解法」的な問題も多く、単なる演習書を超えた面白さがある。

この本で目を引いたのが、以下のような問題である。＊印２つの難問指定。以下引用。

P99** オースト

もっとみる

hydraenids

2024年3月19日 00:56

一様加速する電荷は電磁波を放射するか？―電磁気学の奥深すぎるパラドックス―

はじめに　等加速度運動を相対論的に記述するリンドラー座標について、これまでに以下の5本の記事を書いた。

①リンドラー座標を自力で導出してみた―等加速度運動の相対論的記述―
②リンドラー座標つれづれ(1)―双子のパラドックス―
③一般相対論的放物線―リンドラー座標つれづれ(2)―
④事象の地平面、ガウスの法則の破綻？—リンドラー座標つれづれ(3)―
⑤無限遠にある電荷がガウスの法則を取り戻す―リン

もっとみる

hydraenids

2024年2月11日 10:49

無限遠にある電荷がガウスの法則を取り戻す―リンドラー座標つれづれ(4)—

はじめに　しつこいが、リンドラー座標ネタは続く。本稿は、以下の記事の続きである。

問題をおさらいする。荷電粒子が$${z}$$軸上を相対論的な等加速度運動をしている状況を考える。$${t = -\infty}$$, $${z = +\infty}$$から原点に向かって移動してきて、$${t = 0}$$に$${z = b\,\,(>0)}$$に到達し、そこで折り返して$${t = +\infty

もっとみる

hydraenids

2024年1月23日 01:01

事象の地平面、ガウスの法則の破綻？—リンドラー座標つれづれ(3)―

はじめに　等加速運動を相対論的に記述するリンドラー座標について、これまでに以下の3篇の記事を書いた。

①リンドラー座標を自力で導出してみた―等加速度運動の相対論的記述―
②リンドラー座標つれづれ(1)―双子のパラドックス―
③一般相対論的放物線―リンドラー座標つれづれ(2)―

相対論的な等加速度運動で興味深いのは、等加速度運動する主体が荷電粒子の場合である。荷電粒子の等加速度運動を相対論的に取

もっとみる

hydraenids

2024年1月20日 10:28

$Interference Pattern Formed in a Finger Gap is NOT Single Slit Diffraction$

Interference Pattern Formed in a Finger Gap is NOT Single Slit Diffraction

Simple way of making an interference pattern with fingersThe phenomenon of forming an interference pattern by using light that passed through a double slit is a basic item learnt in a high school phys

もっとみる

hydraenids

2023年12月23日 11:08

一般相対論的放物線—リンドラー座標つれづれ(2)—

はじめに　本稿でも、等加速度運動の相対論的な記述について紹介する。以下の記事の続きである。本稿の内容も、調べればどこかに解説されていることなので、自分のオリジナルな部分は特にない。表式を簡単にするため、前記事同様、以下で光速度$${c=1}$$とする単位系を使用する。

場所に寄らず一様な重力場があるとき、ニュートン力学によると、空中に放り投げた物体の軌道が2次曲線の放物線を描くことは、高校の物理

もっとみる

hydraenids

2023年12月16日 23:43

リンドラー座標系つれづれ(1)―双子のパラドックス―

はじめに　本稿でも、等加速度運動の相対論的な記述について紹介する。以下の記事の続きである。本稿の内容も、調べればどこかに解説されていることなので、自分のオリジナルな部分は特にない。表式を簡単にするため、前記事同様、以下で光速度$${c=1}$$とする単位系を使用する。

ざっと復習すると、静止系（S系）に対して、$${x}$$方向に一定の加速度$${a'}$$で動いている座標系をS'系とすると、S

もっとみる

hydraenids

2023年10月4日 15:20

リンドラー座標を自力で導出してみた―等加速度運動の相対論的記述―

はじめに　1990年に放送されたシリーズもののNHKスペシャル「銀河宇宙オデッセイ」を覚えている人がいたら、いい年した大人だろう。当時最先端の天文学の世界を紹介する科学番組なのだが、当時まだ珍しかったCGを駆使した映像が美しく、とにかくそのクオリティが半端なく高かったのをよく覚えている。当時中学2年の私は天文にハマっており、朝日文庫から出ていたカール・セーガンの「COSMOS」で読んだ世界が、当時

もっとみる

hydraenids

2023年7月15日 23:55

「ビリヤードπ計算機」の熱力学的解法

ビリヤードπ計算機とは、質量の異なる2つの玉を衝突させて、その衝突回数から円周率が求まるという力学的な装置のことである（私が勝手に命名）。
下図のように、水平面上に2つの玉M, m（それぞれ質量を$${M}$$, $${m}$$とし、$${M\ge m}$$）があり、玉Mを静止している玉mに向かって転がすと、玉Mの方が重いため、玉mは、玉Mと壁との間で衝突を繰り返す。

玉Mは、玉mに衝突される度

もっとみる

ちょっと上級の物理学（たまに数学）

フォローしませんか？

記事一覧