
「スモールデータ解析と機械学習」を寄り道写経 ~ 第3章「回帰分析と最小二乗法」
第3章「回帰分析と最小二乗法」
書籍の著者 藤原幸一 先生
この記事は、テキスト「スモールデータ解析と機械学習」第3章「回帰分析と最小二乗法」の通称「寄り道写経」を取り扱います。
今回は寄り道ポイントがてんこ盛り!
テキストを開いてスモールデータの旅に出発です🚀
このシリーズは書籍「スモールデータ解析と機械学習」(オーム社、「テキスト」と呼びます)の機械学習の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。
はじめに
テキスト「スモールデータ解析と機械学習」のご紹介
テキストは、2022年2月に発売され、スモールデータと呼ばれる小さなサンプルサイズのデータを用いた機械学習の取り組み方について、理論(数式)とPythonサンプルプログラムを提案する素晴らしい実用書です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「スモールデータ解析と機械学習」第1版第1刷、著者 藤原幸一、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
第3章 回帰分析と最小二乗法
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
この章の寄り道ポイントです。
1.重回帰
最小二乗法による回帰係数の算出と未知データの予測を様々なPythonパッケージで試します。
2.多重共線性
オリジナルコードが無いテキストの行列計算をPythonで実装します。
3.主成分回帰(PCR)、リッジ回帰、部分的最小二乗法(PLS)
テキストオリジナルコードをscikit-learnで再現してみます。
4.分光分析による物性推定
テキストオリジナルコードをscikit-learnで再現してみます。
この章で使用するライブラリをインポートします。
「テキストオリジナルコード」はオーム社HPからダウンロードできる書籍掲載のプログラムであり、書籍購入者のみ利用できるとのことです。
### インポート
# テキストオリジナルコード
import scale
import linear_regression as linear
from linear_regression import (
least_squares, ls_est, pcr, ridge, nipals_pls1, simpls)
# 数値計算
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# データ取得
import scipy.io
# 最小二乗法・線形回帰
from scipy.linalg import lstsq
import statsmodels.api as sm
# scikit-learn 機械学習
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.cross_decomposition import PLSRegression
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import root_mean_squared_error, make_scorer
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
最小二乗法
プログラム3.2「最小二乗法の数値例」を様々なPythonのパッケージを用いて実装します。
データの作成
テキストのデータを引用いたします。
### データの作成 テキストのデータを引用
# 入力データ
X = np.array([[0.01, 0.50, -0.12],
[0.97, -0.63, 0.02],
[0.41, 1.15, -1.17],
[-1.38, -1.02, 1.27]])
# 出力データ
y = np.array([[0.25], [0.08], [1.03], [-1.37]])
# 未知サンプル
x = np.array([1, 0.7, -0.2])最小二乗法による回帰係数、および、未知データの予測値を算出します。
テキストオリジナルコードによる算出結果は次のとおりです。

では、様々な回帰分析の旅に出発しましょう!
行列計算
回帰係数$${\boldsymbol{\beta}}$$を次の行列計算を用いて算出します。
$${\boldsymbol{\beta}=(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y}}$$
### 行列計算
# 回帰係数の算出
beta = np.linalg.inv(X.T @ X) @ X.T @ y
# 予測値の算出
y_hat = x @ beta
# 結果表示
print('回帰係数:')
print(beta)
print('\n予測値:')
print(y_hat)【実行結果】

numpyの関数
numpyの最小二乗法 lstsq を利用します。
### numpyの関数 ★オリジナル
# 回帰係数の算出
beta = np.linalg.lstsq(X, y, rcond=None)[0]
# 予測値の算出
y_hat = x @ beta
# 結果表示
print('回帰係数:')
print(beta)
print('\n予測値:')
print(y_hat)【実行結果】

scipyの関数
scipyの最小二乗法 lstsq を利用します。
### scipyの関数
# 回帰係数の算出
beta = lstsq(X, y)[0]
# 予測値の算出
y_hat = x @ beta
# 結果表示
print('回帰係数:')
print(beta)
print('\n予測値:')
print(y_hat)【実行結果】

statsmodelsのOLS
statsmodelsの最小二乗法OLSによる回帰分析を行います。
### statsmodelsのOLS
# 回帰分析の実行
lm_result = sm.OLS(endog=y, exog=X).fit()
# 回帰係数の算出
beta = lm_result.params.reshape(-1, 1)
# 予測値の算出
y_hat = lm_result.predict(x)
# 結果表示
print('回帰係数:')
print(beta)
print('\n予測値:')
print(y_hat)【実行結果】

scilit-learnのLinearRegression
scilit-learnの線形回帰LinearRegressionによる回帰分析を行います。
### scilit-learnのLinearRegression
# 回帰分析の実行
lr_result = LinearRegression(fit_intercept=False).fit(X, y)
# 回帰係数の算出
beta = lr_result.coef_[0].reshape(-1, 1)
# 予測値の算出
y_hat = lr_result.predict(x.reshape(1, -1))[0]
# 結果表示
print('回帰係数:')
print(beta)
print('\n予測値:')
print(y_hat)【実行結果】


多重共線性と条件数
テキストの3.7節「多重共線性の問題」に取り組みます。
■ 行列のランクと逆行列
最初の取り組みテーマは、テキストの行列A~Cのデータを引用して、ランクと逆行列を算出することです。
まずはフルランクの行列A、Bです。
numpy.linalgのmatrix_rank()でランクを、inv()で逆行列を算出します。
### フルランク(線形独立)の行列には逆行列がある ★テキスト62ページの式(3.58)
A = np.array([[2.01, 1], [4, 2.01]])
B = np.array([[1.99, 1], [4, 2.02]])
print('行列A:')
print(A)
print('ランク:', np.linalg.matrix_rank(A))
print('逆行列:')
print(np.linalg.inv(A).round(2))
print('\n行列B:')
print(B)
print('ランク:', np.linalg.matrix_rank(B))
print('逆行列:')
print(np.linalg.inv(B).round(2))【実行結果】
テキスト62ページに掲載の式(3.58)の逆行列と「ほぼ」同じ結果になりました。

続いてフルランクでない行列Cです。
### Cは行列式がゼロの正方行列=シンギュラー行列 ★テキスト63ページの式(3.59)
C = np.array([[2, 1], [4, 2]])
print('行列C:')
print(C)
print('ランク:', np.linalg.matrix_rank(C))
### 以下はエラーになるためコメントアウトしておく
### LinAlgError: Singular matrix
# print('逆行列:')
# print(np.linalg.inv(C).round(2))【実行結果】
コメントアウトした「print(np.linalg.inv(C).round(2))」を実行すると、「非正則行列エラー」になります。

行列A、B、Cの条件数を算出します。
numpy.linalgのcond()を利用します。
### 行列A、B、Cの条件数 ★テキスト63ページの条件数
print(f'行列Aの条件数: {np.linalg.cond(A):18.0f}')
print(f'行列Bの条件数: {np.linalg.cond(B):18.0f}')
print(f'行列Cの条件数: {np.linalg.cond(C):18.0f}')【実行結果】
テキスト63ページに掲載の条件数と「ほぼ」同じ結果になりました。
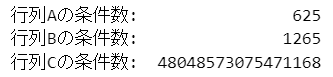
■ 多重共線性と回帰係数
次のテーマに移ります。
説明変数の多重共線性の有無による回帰係数の相違について、プログラム3.3および3.4の考え方をお借りしつつ、確認したいと思います。
多重共線性がある場合、回帰係数が安定しない状況になります!
まずは「多重共線性がない」場合から。
テキストのデータを引用いたします。
### データの定義 テキストのデータを引用
X1 = np.array([[0.01, 0.50, -0.12],
[0.97, -0.63, 0.02],
[0.41, 1.15, -1.17],
[-1.38, -1.02, 1.27]])
X2 = np.array([[-0.01, 0.52, -0.12],
[0.96, -0.64, 0.03],
[0.43, 1.14, -1.17],
[-1.38, -1.01, 1.27]])
y = np.array([0.25, 0.08, 1.03, -1.37]).reshape(-1, 1)データX1とX2それぞれの相関係数を確認します。
### X1とX2の相関係数
print('X1の各列の相関行列:')
print(np.corrcoef(X1, rowvar=False))
print('\nX2の各列の相関行列:')
print(np.corrcoef(X2, rowvar=False))【実行結果】
X1もX2も相関係数の大きい説明変数がありそうです。

続いて行列$${\boldsymbol{X}^{\top} \boldsymbol{X}}$$の条件数を算出します。
### 行列X1.T @ X1, X2.T @ x2の条件数
print(f'行列 X1.T @ X1 の条件数: {np.linalg.cond(X1.T @ X1):7.2f}')
print(f'行列 X2.T @ X2 の条件数: {np.linalg.cond(X2.T @ X2):7.2f}')【実行結果】
テキスト65ページに掲載の条件数に「まあまあ」同じ結果になりました。
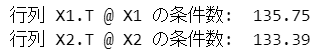
最後にX1とX2の回帰係数を算出します。
テキストのプログラム3.3「多重共線性がないデータの場合」をnumpyを使って書き換えました。
### X1, X2の回帰係数の計算 ★numpy関数使用
beta1 = np.linalg.lstsq(X1, y, rcond=None)[0]
print('beta1:')
print(beta1)
beta2 = np.linalg.lstsq(X2, y, rcond=None)[0]
print('\nbeta2:')
print(beta2)【実行結果】
テキストのプログラム3.3の結果と同じになりました。
多重共線性がない場合、ほぼ同一の回帰係数を得られます。

では「多重共線性がある」場合に移ります。
テキストのデータを引用いたします。
多重共線性がない場合のデータに良く似ています。
### データの定義 テキストのデータを引用
X1 = np.array([[-1.12, -0.51, 0.69],
[-0.43, -1.12, 1.02],
[0.37, 1.10, -0.98],
[1.19, 0.53, -0.73]])
X2 = np.array([[-1.12, -0.51, 0.70],
[-0.43, -1.12, 1.01],
[0.36, 1.10, -0.98],
[1.20, 0.53, -0.73]])
y = np.array([0.40, 1.17, -1.14, -0.42]).reshape(-1, 1)データX1とX2それぞれの相関係数を確認します。
### X1とX2の相関係数
print('X1の各列の相関行列:')
print(np.corrcoef(X1, rowvar=False))
print('\nX2の各列の相関行列:')
print(np.corrcoef(X2, rowvar=False))【実行結果】
X1もX2も相関係数の大きい説明変数がありそうです。
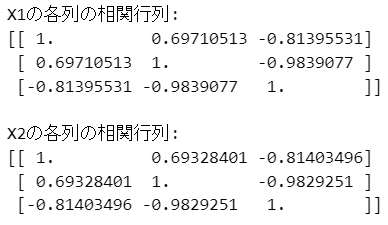
続いて行列$${\boldsymbol{X}^{\top} \boldsymbol{X}}$$の条件数を算出します。
### 行列X1.T @ X1, X2.T @ X2の条件数
print(f'行列 X1.T @ X1 の条件数: {np.linalg.cond(X1.T @ X1):7.2f}')
print(f'行列 X2.T @ X2 の条件数: {np.linalg.cond(X2.T @ X2):7.2f}')【実行結果】
テキスト66ページに掲載の条件数に「まあまあ」同じ結果になりました。
多重共線性がある場合、行列$${\boldsymbol{X}^{\top} \boldsymbol{X}}$$の条件数は「悪い」ようです。
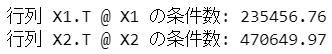
最後にX1とX2の回帰係数を算出します。
テキストのプログラム3.3「多重共線性がないデータの場合」をnumpyで改造します。
### X1, X2の回帰係数の計算 ★numpy関数使用
beta1 = np.linalg.lstsq(X1, y, rcond=None)[0]
print('beta1:')
print(beta1)
beta2 = np.linalg.lstsq(X2, y, rcond=None)[0]
print('\nbeta2:')
print(beta2)【実行結果】
テキストのプログラム3.4の結果と同じになりました。
多重共線性がある場合、2つのサンプルX1・X2から算出した回帰係数は全く異なる値になってしまいました。


主成分回帰(PCR)
テキストの3.10節「主成分回帰(PCR)」に取り組みます。
主成分回帰のアイデアは、説明変数どうしを無相関にすることで多重共線性の問題を回避する点にあります。
主成分分析(PCA)の主成分得点どうしは無相関です。
主成分回帰は、説明変数を主成分分析にかけて主成分得点を取得し、主成分得点で線形回帰を行うアルゴリズムなのです。
テキストのPCR実行プログラム3.6(主成分数=2)とプログラム3.7(主成分数=1)をscikit-learnで改造します。
テキストの多重共線性があるデータを引用いたします。
### データの定義 テキストのデータを引用
X1 = np.array([[-1.12, -0.51, 0.69],
[-0.43, -1.12, 1.02],
[0.37, 1.10, -0.98],
[1.19, 0.53, -0.73]])
X2 = np.array([[-1.12, -0.51, 0.70],
[-0.43, -1.12, 1.01],
[0.36, 1.10, -0.98],
[1.20, 0.53, -0.73]])
y = np.array([0.40, 1.17, -1.14, -0.42]).reshape(-1, 1)主成分数が2のPCRを実行して回帰係数を算出します。
scikit-learnにPCRは無さそうなので、PCAとLinearRegressionの合わせ技で実装します。
PCRの回帰係数はPCAのローディング行列と線形回帰の回帰係数の行列積で求めます。
### scikit-learnのPCR利用 主成分数2
# 主成分数
n_components = 2
# パイプラインの設定
pipeline = Pipeline(steps=[
('pca', PCA(n_components=n_components)), # PCA
('regressor', LinearRegression(fit_intercept=False)), # 線形回帰
])
## X1の回帰係数の算出
# 学習
PCR_model1 = pipeline.fit(X1, y)
# PCAの結果、線形回帰の結果を取得
pca_result1 = PCR_model1.named_steps['pca']
regressor_result1 = PCR_model1.named_steps['regressor']
# PCAのローディング行列の取得
loadings1 = pca_result1.components_
# 線形回帰の回帰係数を取得
beta_lr1 = regressor_result1.coef_[0].reshape(-1, 1)
# PCRの回帰係数の算出
beta1 = loadings1.T @ beta_lr1
print('beta1')
print(beta1)
## X2の回帰係数の算出
# 学習
PCR_model2 = pipeline.fit(X2, y)
# PCAの結果、線形回帰の結果を取得
pca_result2 = PCR_model2.named_steps['pca']
regressor_result2 = PCR_model2.named_steps['regressor']
# PCAのローディング行列の取得
loadings2 = pca_result2.components_
# 線形回帰の回帰係数を取得
beta_lr2 = regressor_result2.coef_[0].reshape(-1, 1)
# PCRの回帰係数の算出
beta2 = loadings2.T @ beta_lr2
print('\nbeta2')
print(beta2)【実行結果】
テキストの実行結果と「ほぼ」同じ値になりました。
2つのデータX1、X2の回帰係数はほぼ同じ値になり、多重共線性が回避されたことが分かります。

続いて、主成分数が1のPCRを実行して回帰係数を算出します。
「n_components = 1」とし、その他のコードは主成分数が2と同じです。
### scikit-learnのPCR利用 主成分数1 ★オリジナル
# 主成分数
n_components = 1
# パイプラインの設定
pipeline = Pipeline(steps=[
('pca', PCA(n_components=n_components)), # PCA
('regressor', LinearRegression(fit_intercept=False)), # 線形回帰
])
## X1の回帰係数の算出
# 学習
PCR_model1 = pipeline.fit(X1, y)
# PCAの結果、線形回帰の結果を取得
pca_result1 = PCR_model1.named_steps['pca']
regressor_result1 = PCR_model1.named_steps['regressor']
# PCAのローディング行列の取得
loadings1 = pca_result1.components_
# 線形回帰の回帰係数を取得
beta_lr1 = regressor_result1.coef_[0].reshape(-1, 1)
# PCRの回帰係数の算出
beta1 = loadings1.T @ beta_lr1
print('beta1')
print(beta1)
## X2の回帰係数の算出
# 学習
PCR_model2 = pipeline.fit(X2, y)
# PCAの結果、線形回帰の結果を取得
pca_result2 = PCR_model2.named_steps['pca']
regressor_result2 = PCR_model2.named_steps['regressor']
# PCAのローディング行列の取得
loadings2 = pca_result2.components_
# 線形回帰の回帰係数を取得
beta_lr2 = regressor_result2.coef_[0].reshape(-1, 1)
# PCRの回帰係数の算出
beta2 = loadings2.T @ beta_lr2
print('\nbeta2')
print(beta2)【実行結果】
テキストの実行結果とほぼ同じ値になりました。
2つのデータX1、X2の回帰係数はほぼ同じ値になり、多重共線性が回避されたことが分かります。


リッジ回帰
テキストの3.11節「リッジ回帰」に取り組みます。
リッジ回帰のアイデアは、パイパーパラメータ$${\mu}$$の導入により、正規方程式の行列$${\boldsymbol{X}^{\top} \boldsymbol{X}}$$の条件数を改善させて、逆行列計算を安定させる点にある、とテキストは説明します。
通常の最小二乗法の回帰係数算出には$${\boldsymbol{X}^{\top} \boldsymbol{X}}$$の逆行列を使います。
一方でリッジ回帰では、$${\boldsymbol{X}^{\top} \boldsymbol{X} + \mu \boldsymbol{I}}$$の逆行列を使います。
対角成分に$${\mu}$$を加えることで、行列$${\boldsymbol{X}^{\top} \boldsymbol{X}}$$のトレース(固有値の和)を大きくし、最小固有値が$${\mu}$$だけ大きくなります。
最小固有値が大きくなると最小特異値が大きくなるので、行列の条件数が小さくなり、逆行列計算の条件が良くなる、ということのようです。
テキストのリッジ回帰実行プログラム3.9「リッジ回帰の数値例」をscikit-learnで改造します。
テキストの多重共線性があるデータを引用いたします。
### データの定義 テキストのデータを引用
X1 = np.array([[-1.12, -0.51, 0.69],
[-0.43, -1.12, 1.02],
[0.37, 1.10, -0.98],
[1.19, 0.53, -0.73]])
X2 = np.array([[-1.12, -0.51, 0.70],
[-0.43, -1.12, 1.01],
[0.36, 1.10, -0.98],
[1.20, 0.53, -0.73]])
y = np.array([0.40, 1.17, -1.14, -0.42]).reshape(-1, 1)行列$${\boldsymbol{X}^{\top} \boldsymbol{X} + \mu \boldsymbol{I}}$$の条件数を算出します。
### 行列X1.T @ X1 + 0.1I, X1.T @ X1 + Iの条件数
print('行列 X1.T @ X1 +0.1I の条件数: '
f'{np.linalg.cond(X1.T @ X1 + 0.1 * np.eye(X1.shape[1])):7.2f}')
print('行列 X1.T @ X1 +I の条件数 : '
f'{np.linalg.cond(X1.T @ X1 + 1 * np.eye(X1.shape[1])):7.2f}')【実行結果】
テキスト80ページの条件数と「ほぼ」同じ値になりました。
パラメータ$${\mu}$$を導入することで、条件数が小さくなることが分かりました。
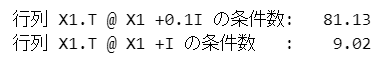
$${\mu=0.1}$$のリッジ回帰を実行して回帰係数を算出します。
scikit-learnのRidgeを利用します。
### scikit-learnのRidge利用 alpha=0.1
# パラメータαに0.1を設定
alpha = 0.1
# X1の学習
ridge_model1 = Ridge(alpha=alpha, fit_intercept=False)
ridge_fitted1 = ridge_model1.fit(X1, y)
# X1の回帰係数の表示
print('beta1:')
print(ridge_fitted1.coef_[0].reshape(-1, 1))
# X2の学習
ridge_model2 = Ridge(alpha=alpha, fit_intercept=False)
ridge_fitted2 = ridge_model2.fit(X2, y)
# X2の回帰係数の表示
print('\nbeta2:')
print(ridge_fitted2.coef_[0].reshape(-1, 1))【実行結果】
テキストの実行結果と同じ値になりました。
2つのデータX1、X2の回帰係数はほぼ同じ値になり、多重共線性が回避されたことが分かります。

続いて、$${\mu=1}$$のリッジ回帰を実行して回帰係数を算出します。
「alpha = 1」とし、その他のコードは$${\mu=0.1}$$と同じです。
# パラメータαに1を設定
alpha = 1
# X1の学習
ridge_model1 = Ridge(alpha=alpha, fit_intercept=False)
ridge_fitted1 = ridge_model1.fit(X1, y)
# X1の回帰係数の表示
print('beta1:')
print(ridge_fitted1.coef_[0].reshape(-1, 1))
# X2の学習
ridge_model2 = Ridge(alpha=alpha, fit_intercept=False)
ridge_fitted2 = ridge_model2.fit(X2, y)
# X2の回帰係数の表示
print('\nbeta2:')
print(ridge_fitted2.coef_[0].reshape(-1, 1))【実行結果】
テキストの実行結果と同じ値になりました。
2つのデータX1、X2の回帰係数はほぼ同じ値になり、多重共線性が回避されたことが分かります。


部分的最小二乗法(PLS)
テキストの3.12から3.17節の「部分的最小二乗法(PLS)」に取り組みます。
テキストが「スモールデータの線形回帰モデルの学習アルゴリズム」としておすすめするのが部分的最小二乗法(PLS)です。
PLSは主成分回帰(PCR)のように説明変数の次元削減を行います。
ただPCRといい意味で異なるのは、PLSの次元削減の際、説明変数に加えて目的変数を活用することで、説明変数と目的変数の相関関係を考慮できる点だそうです。
詳しい説明はテキストをぜひお読みください!
テキストのPLS実行プログラム3.11「PLS1の数値」をscikit-learnで改造します。
テキストの多重共線性があるデータを引用いたします。
### データの定義 テキストのデータを引用
X1 = np.array([[-1.12, -0.51, 0.69],
[-0.43, -1.12, 1.02],
[0.37, 1.10, -0.98],
[1.19, 0.53, -0.73]])
X2 = np.array([[-1.12, -0.51, 0.70],
[-0.43, -1.12, 1.01],
[0.36, 1.10, -0.98],
[1.20, 0.53, -0.73]])
y = np.array([0.40, 1.17, -1.14, -0.42]).reshape(-1, 1)$${R=2}$$のPLSを実行して回帰係数を算出します。
scikit-learnのPLSRegressionを利用します。
注意点です。
PLSRegressionには切片を使うかどうかの引数が無さそうなので、切片ありで学習する作りになりました。
テキストのモデルは切片無しなので、テキストとPLSRegressionの結果は相違してしまいます。
### scikit-learnのPLS利用 主成分数2 ※切片を外せない
## 主成分数が2のとき
n_components = 2
# X1の学習
PLS_model1 = PLSRegression(n_components=n_components)
PLS_result1 = PLS_model1.fit(X1, y)
# X1の回帰係数の表示
print('beta1:')
print(PLS_result1.coef_[0].reshape(-1, 1))
# X2の学習
PLS_model2 = PLSRegression(n_components=n_components)
PLS_result2 = PLS_model2.fit(X2, y)
# X1の回帰係数の表示
print('\nbeta2:')
print(PLS_result2.coef_[0].reshape(-1, 1))【実行結果】
テキストの実行結果と「だいたい」同じ値になりました。
2つのデータX1、X2の回帰係数はほぼ同じ値になり、多重共線性が回避されたことが分かります。

続いて、$${R=1}$$のPLSを実行して回帰係数を算出します。
「n_components = 1」とし、その他のコードは$${R=2}$$と同じです。
## 主成分数が1のとき
n_components = 1
# X1の学習
PLS_model1 = PLSRegression(n_components=n_components)
PLS_result1 = PLS_model1.fit(X1, y)
# X1の回帰係数の表示
print('beta1:')
print(PLS_result1.coef_[0].reshape(-1, 1))
# X2の学習
PLS_model2 = PLSRegression(n_components=n_components)
PLS_result2 = PLS_model2.fit(X2, y)
# X1の回帰係数の表示
print('\nbeta2:')
print(PLS_result2.coef_[0].reshape(-1, 1))【実行結果】
テキストの実行結果と「だいたい」同じ値になりました。
2つのデータX1、X2の回帰係数はほぼ同じ値になり、多重共線性が回避されたことが分かります。


ケーススタディ「分光分析による物性推定」
3.20節「分光分析による物性推定」のケーススタディに取り組みます。
オープンデータ「ディーゼル燃料のNIRスペクトルデータ」を用いて、リッジ回帰、PCR、PLSを実践します。
説明変数の数(列数)がサンプルサイズ(行数)よりも大きいデータです!
寄り道写経的には、①テキストオリジナルコードのエラー・ワーニング対策と、②scikit-learnでの実装に取り組みます!
① エラー・ワーニング対策
プログラム3.20「リッジ回帰とPCRでの検量線の学習」とプログラム3.21「PLSでの検量線の学習」で発生するワーニングの対策案を考えてみます。
■ ワーニング発生例1
テキストオリジナルコードのリッジ回帰、PLS、PLSで発生します。
リッジ回帰を例にして検討しましょう。
# リッジ回帰
beta = linear.ridge(X_, y_, mu=1)
y_hat_ = Xval_ @ beta
y_hat = scale.rescaling(y_hat_, meany, stdy)
rmse, r = linear.pred_eval(yval, y_hat, plotflg=True)【ワーニングメッセージ(部分)】
RuntimeWarning: Degrees of freedom <= 0 for slice
RuntimeWarning: divide by zero encountered in divide
RuntimeWarning: invalid value encountered in multiply
【実行結果】
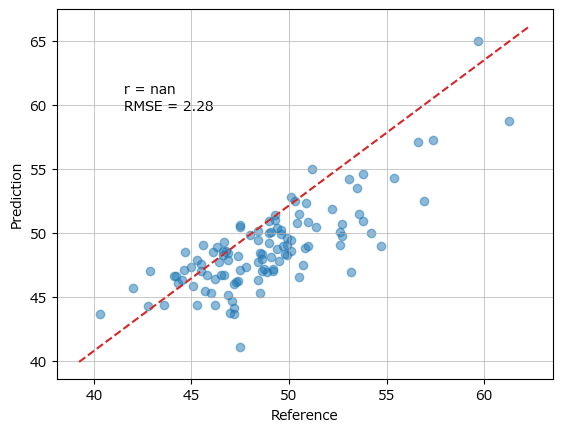
上記のワーニングメッセージが表示され、グラフの相関係数 r が nan になる現象の対策です。
【対策の概要】
RMSEおよび相関係数を算出する関数「linear.pred_eval」に与える目的変数の正解値 yval と予測値 y_hat を ravel() または flatten() で平坦化します。
【コード変更(案)】
# リッジ回帰 ★部分を改造
beta = linear.ridge(X_, y_, mu=1)
y_hat_ = Xval_ @ beta
y_hat = scale.rescaling(y_hat_, meany, stdy)
rmse, r = linear.pred_eval(yval.ravel(), y_hat.ravel(), plotflg=True) # ★ravel【変更後の実行結果】
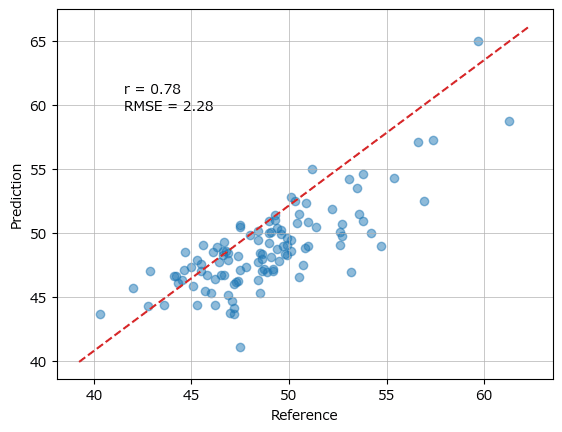
■ ワーニング発生例2
テキストオリジナルコードのPCR実行時のワーニングです。
# PCR
beta = (linear.pcr(X_, y_, R=5))
y_hat_ = Xval_ @ beta
y_hat = scale.rescaling(y_hat_, meany, stdy)
rmse, r = linear.pred_eval(yval.ravel(), y_hat.ravel(), plotflg=True) # ★ravel【ワーニングメッセージ(部分)】
ComplexWarning: Casting complex values to real discards the imaginary part
return math.isfinite(val)
ComplexWarning: Casting complex values to real discards the imaginary part
offsets = np.asanyarray(offsets, float)
【実行結果】
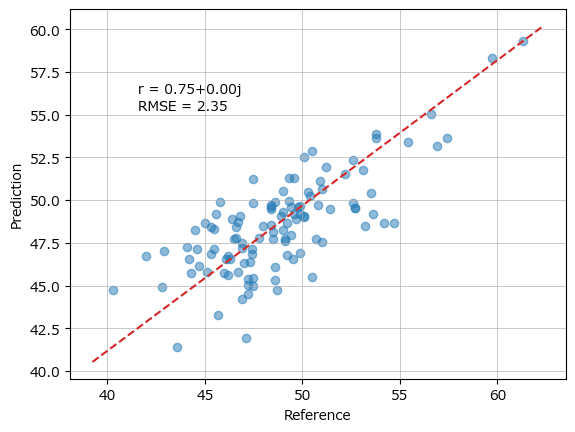
上記のワーニングメッセージが表示され、グラフの相関係数 r に +0.00j が付加される現象の対策です。
【対策の概要】
pcr実行関数「linear.pcr」の戻り値「回帰係数」から「実数部」のみ取り出します。
「0.00j」は虚数です。
【コード変更(案)】
# PCR ★部分を改造
beta = (linear.pcr(X_, y_, R=5)).real # ★虚数を除外するため、実部realを取り出し
y_hat_ = Xval_ @ beta
y_hat = scale.rescaling(y_hat_, meany, stdy)
rmse, r = linear.pred_eval(yval.ravel(), y_hat.ravel(), plotflg=True) # ★ravel【変更後の実行結果】

② scikit-learnによる実装
プログラム3.20「リッジ回帰とPCRでの検量線の学習」とプログラム3.21「PLSでの検量線の学習」のリッジ回帰、PCR、PLSを scikit-learnで実装してみます。
プログラム3.19まで実行した後に、scikit-learn 版を実行しましょう。
■ プロット関数の定義
### プロット関数の定義
def plot_scatter(y_true, y_pred, r, rmse):
plt.scatter(y_true, y_pred, alpha=0.5)
plt.plot([y_true.min(), y_true.max()], [y_pred.min(), y_pred.max()],
color='tab:red', ls='--')
plt.grid(lw=0.5)
plt.xlabel('$Y$ 観測値')
plt.ylabel('$Y$ 予測値')
plt.title(f'r = {r:.2f}, RMSE = {rmse:.2f}');■ リッジ回帰
### scikit-learnのRidge利用
# 学習
result = Ridge(alpha=1, fit_intercept=False).fit(X_, y_)
# 予測
y_hat_ = result.predict(Xval_)
y_hat = scale.rescaling(y_hat_, meany, stdy)
# 評価指標 RMSE, 相関係数r
rmse = root_mean_squared_error(yval, y_hat)
r = np.corrcoef(yval.ravel(), y_hat.ravel())[0, 1]
# プロット
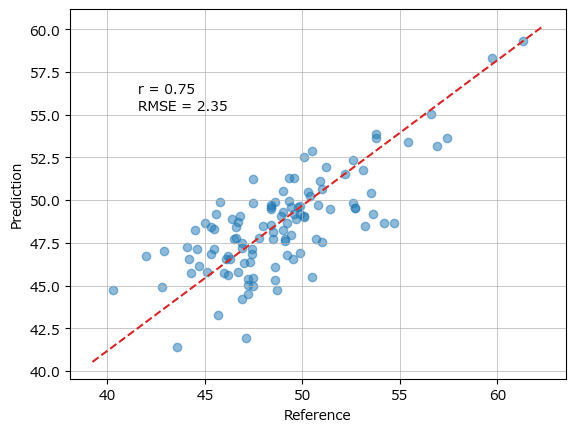
plot_scatter(yval, y_hat, r, rmse)【実行結果】
相関係数、RMSEはテキストの値と同じになりました。
■ PCR
### scikit-learnのPCAとLinearRegressionでPCRを実行 ★オリジナル
# 主成分数
n_components = 5
# パイプラインの設定
pipeline = Pipeline(steps=[
('pca', PCA(n_components=n_components)), # PCA
('regressor', LinearRegression(fit_intercept=False)), # 線形回帰
])
# 学習
result = pipeline.fit(X_, y_)
# 予測
y_hat_ = result.predict(Xval_)
y_hat = scale.rescaling(y_hat_, meany, stdy)
# 評価指標 RMSE, 相関係数r
rmse = root_mean_squared_error(yval, y_hat)
r = np.corrcoef(yval.ravel(), y_hat.ravel())[0, 1]
# プロット
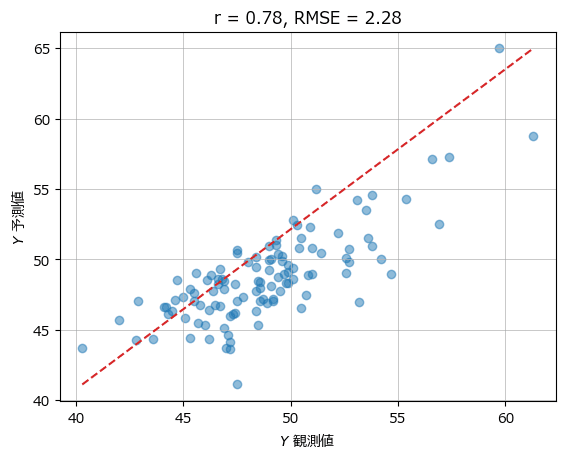
plot_scatter(yval, y_hat, r, rmse)【実行結果】
相関係数、RMSEはテキストの値と同じになりました。
■ PLS 主成分数=5
### scikit-learnのPLS利用 n_components=5
# 主成分数
n_components = 5
# 学習
result = PLSRegression(n_components=n_components)
result.fit(X_, y_)
# 予測
y_hat_ = result.predict(Xval_)
y_hat = scale.rescaling(y_hat_, meany, stdy)
# 評価指標 RMSE, 相関係数r
rmse = root_mean_squared_error(yval, y_hat)
r = np.corrcoef(yval.ravel(), y_hat.ravel())[0, 1]
# プロット
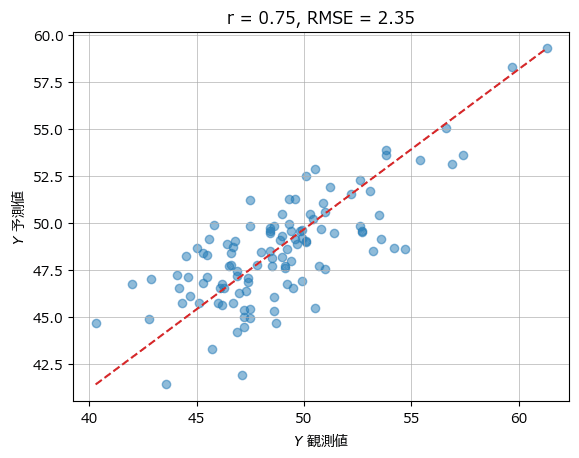
plot_scatter(yval, y_hat, r, rmse)【実行結果】
相関係数、RMSEはテキストの値と同じになりました。
■ PLSの最適な主成分数の探索
GridSearchCV で主成分数 n_components を探索します。
テキストの評価指標 PRESS を make_scorer() を用いて実装してみました。
うまく計算できているかは不明です・・・
### scikit-learnのGridSearchCV利用 最適なn_componentsを探索
# 評価指標PRESSの算出関数の定義
def calc_press(y_true, y_pred):
return sum((y_true - y_pred)**2)
# 探索するパラメータの設定
params = {'n_components': list(range(1, 31))} # n_components:1~30を探索
# ユーザー定義評価指標の設定
press = make_scorer(score_func=calc_press, greater_is_better=False)
# estimatorの設定
estimator = PLSRegression()
# GridSearchCVの設定
grid_search = GridSearchCV(estimator, params, cv=10, scoring=press) # 10foldCV
# GridSearchCVの実行
grid_search.fit(X_, y_)
# 最適なn_componentsの取り出し
best_n_components = grid_search.best_params_['n_components']
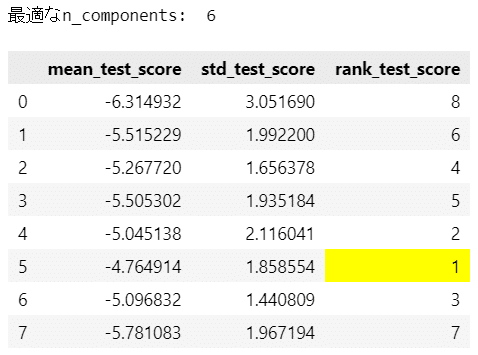
print('最適なn_components: ', best_n_components)
# cvの結果を表示
display(pd.DataFrame(grid_search.cv_results_).iloc[:8, 16:]
.style.map(lambda x: 'background-color: yellow' if x==1 else ''))【実行結果】
最適な主成分数は 6 でした。
テキストの最適な主成分数は7です。
■ PLS 主成分数=6(最適な主成分数)
### scikit-learnのPLS利用 n_components=最適値6
# 学習
result = PLSRegression(n_components=best_n_components)
result.fit(X_, y_)
# 予測
y_hat_ = result.predict(Xval_)
y_hat = scale.rescaling(y_hat_, meany, stdy)
# 評価指標 RMSE, 相関係数r
rmse = root_mean_squared_error(yval, y_hat)
r = np.corrcoef(yval.ravel(), y_hat.ravel())[0, 1]
# プロット
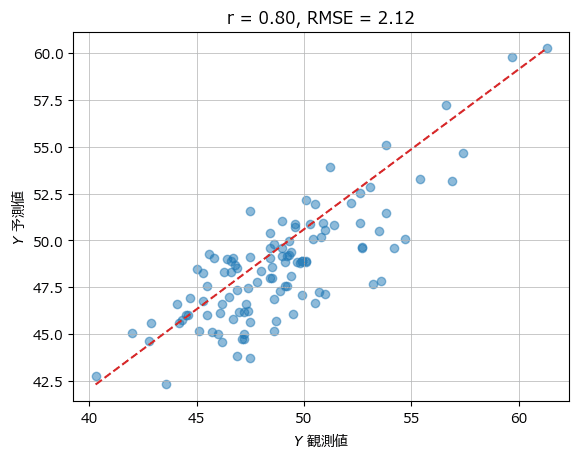
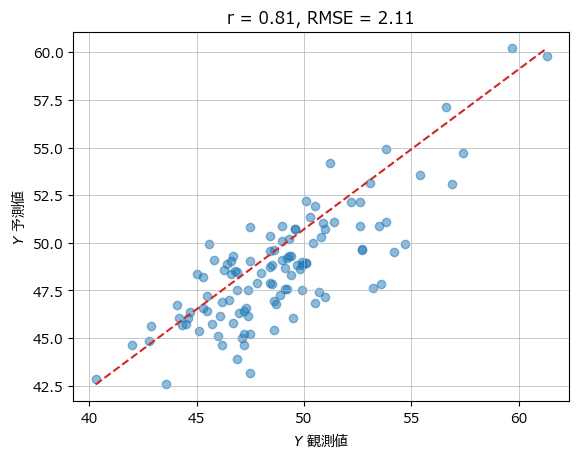
plot_scatter(yval, y_hat, r, rmse)【実行結果】
テキストには主成分数=6の実行結果が掲載されていないため、テキストとの結果比較はできません。
■ PLS 主成分数=7
### scikit-learnのPLS利用 n_components=7 ★オリジナル
# 主成分数
n_components = 7
# 学習
result = PLSRegression(n_components=n_components)
result.fit(X_, y_)
# 予測
y_hat_ = result.predict(Xval_)
y_hat = scale.rescaling(y_hat_, meany, stdy)
# 評価指標 RMSE, 相関係数r
rmse = root_mean_squared_error(yval, y_hat)
r = np.corrcoef(yval.ravel(), y_hat.ravel())[0, 1]
# プロット
plot_scatter(yval, y_hat, r, rmse)【実行結果】
相関係数、RMSEはテキストの値と同じになりました。

第3章の寄り道写経は以上です。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
