見出し画像

第12章「悲しいときこそ笑顔？」のベイズモデリングをPyMC Ver.5 で

ネイピア DS

この記事は、テキスト「たのしいベイズモデリング２」の第12章「悲しいときこそ笑顔？」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

この章では、心理学研究の再現可能性という硬派なテーマを取り扱います。
「笑顔を作ると漫画がいっそう面白く感じられる」という研究成果に対する複数の追試実験結果を分析するのです！

今回の PyMC化 は、テキストとデータ前処理が異なるため、テキストの結果と比較することができませんでした。
ただ、やれることを精一杯やれたのでヨシとします。

喜ぶ会社員たちのイラスト：「いらすとや」さんより

ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。


サマリー

テキストの概要

執筆者　　　：　馬景昊 先生
モデル難易度：　★★・・・　（やさしめ）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★・ & ほぼ納得 \\
結果再現度 & ★★★★・ & ほぼ納得 \\
楽しさ & ★★★★★ & 楽しい！ \\
\end{array}
$$

花型の評価印のイラスト

評価ポイント

  • この章の最難関はデータセットの整備です。
    着手時点でデータセットを作る手立てが見つからず、数日間悩んで、一時はこの章を棄権するつもりでした。
    データなくして推論なし、です。
    ところが、ひょんなことからデータセットの取得・作成方法を発見でき、なんとかモデル化に漕ぎ着けることができました。
    運が良かったです！

工夫・喜び・反省

  • テキストは「表」を多用しています。
    Pythonの表と言えばPandas。
    テキストの複雑な表加工に取り組んだことが奏功して、Pandasの未知の機能「マルチインデックス・マルチカラム」を使えるようになりました。

カレンダーのテンプレート：「いらすとや」さんより

モデルの概要

テキストの調査・実験の概要

■ 表情フィードバック仮説
「悲しいから泣く」のではなく「泣くから悲しい」…
身体的変化が感情（情動）を変化させるという仮説です。
詳しくはWikipediaで！

いろいろな表情の映画を見る人のイラスト（男性）：「いらすとや」さんより

■ 表情フィードバック仮説の検証実験
1988年、ドイツの心理学者ストラック博士らが表情フィードバック仮説を支持する検証結果を得たとする研究論文を発表しました。
口にペンを加えて疑似笑顔を作った実験グループは、笑顔を作らないグループよりも漫画が面白く感じられた、とする実験結果を得たのです。
テキストによるとこの論文は2019年2月25日までに Google Scholar 上で 1938回も引用されたそうです。
影響力の高い論文と言えるのでしょう。

次の図はBayesian Spectaclesサイトより引用しました。
2016年に別の研究論文に掲載された実験の様子を参考にさせていただきます。
人がペンを口にくわえています。
左が口を横に広げる疑似笑顔の「実験群」、右が口をとがらせる「対照群」です。
口を横に広げる実験群の人の方が漫画を面白く感じたなら、表情フィードバック仮説の裏付けになるとのこと。

引用元サイト: https://www.bayesianspectacles.org/musings-on-preregistration/

■ 研究成果の再現可能性
少々、話題が変わります。
テキストによると2010年代、心理学の研究成果に対する再現可能性の問題・事件が次々と発生したそうです。
再現できない研究があったり、中にはデータ改ざん・捏造があったりと、さまざまな議論が巻き起こっているそうです。

このような状況下、ストラック博士は1988年の表情フィードバック仮説検証実験の追加試験を研究者たちに呼びかけました。
世界中の17の研究室が追試に参加したそうです。
その結果は「再現が得られなかった」とのこと。

なお2019年、ストラック博士は論文～再現性の一連の状況に関して、イグ・ノーベル心理学賞を受賞しました。

■ テキストの分析の概要
テキストはストラック博士等の1988年の論文に関する17研究室の追試結果データを用いて、実験群「口を横に広げるグループ」（疑似笑顔）と対照群「口をとがらせるグループ」の採点値（平均値）を分析して、実験群の採点が対照群よりも高いという研究仮説の「効果の有無」を確認します。

いろいろな表情の映画を見る人のイラスト（男性）：「いらすとや」さんより

ここまでの流れを図示します（３記事ぶりのポンチ絵！）

■ 分析対象データの概要
Open Science Framework （OSF）サイトに格納された17研究室の追試結果データ「RRR - Strack et al (1988)」のページです。
データの概要が掲載されています。

このサイトより「Data_FINAL.zip」をダウンロードします。

画面右側の「︙」をクリックするとダウンロードメニューを表示できます。

OSFのData_FINAL.zipダウンロード画面より引用

そして、ダウンロードしたzipファイルに含まれるcsvファイルを統合してデータの前処理を行う R スクリプトも提供されています。

【注意事項１】
テキストの配布コードにデータは含まれていません。
読者自身で上記サイトのデータをダウンロードし、データ前処理まで済ませておく必要があります。

【注意事項２】
自環境だけの問題かもしれませんが、データの前処理を行う R スクリプトを実行したところ、エラーが発生して、結果として、モデルに入力可能なデータを作ることができませんでした。

愛想笑いのイラスト：「いらすとや」さんより

■ データ作成の代替策
別件で PyMC と連携可能なベイズモデリングインターフェースの Bambi サイトに訪れたところ、Example ページに追試データの前処理のサンプルコードを発見しました（号泣）
この記事もこのサンプルコードを利用いたしました。
Bambiさん、ありがとうございます！

子鹿・バンビのイラスト：「いらすとや」さんより

テキストのモデリング

■ 目的変数と関心のあるパラメータ
目的変数は実験群・対照群別、研究室別の「採点値$${\boldsymbol{x_i}}$$」です。
添字$${i}$$は研究室IDです。
関心のあるパラメータは、実験群または対照群全体の平均値$${\mu}$$などです。
また、実験群・対照群別、および研究室別に非重複度、優越率を算出いたします。

■ モデル数式
テキストでは「研究室をレベルと設定する階層線形モデル」と称されています。

$$
\begin{align*}
x_{i実験群} &\sim \text{Normal}\ (\mu_{i実験群},\ \sigma) \\
x_{i対照群} &\sim \text{Normal}\ (\mu_{i対照群},\ \sigma) \\
\mu_{i実験群} &\sim \text{Normal}\ (\mu_{実験群},\ \tau) \\
\mu_{i対照群} &\sim \text{Normal}\ (\mu_{対照群},\ \tau) \\
\end{align*}
$$

テキストの数式を一部改変して引用

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。

学ぶ人工知能のイラスト：「いらすとや」さんより

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats

# PyMC
import pymc as pm
import arviz as az

# ファイル操作
from glob import glob

# 描画
import matplotlib.pyplot as plt
# import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込みと前処理
予めOSFサイトよりデータダウンロードして、csvファイルを展開しておきます。
ファイル名「凛dogru_Data.csv」は「Ozdogru_Data.csv」に手作業で変更しておきます。

続いて、Pythonコードでcsvファイルを統合します。
以下のコードは先程紹介した Bambi ・ Exampe のサンプルコードを引用いたしました。

### データの読み込み
# 引用サイト
# https://bambinos.github.io/bambi/notebooks/Strack_RRR_re_analysis.html

## 初期値設定
# 17ファイルのパスを設定
DL_PATH = './data/*.csv'
# 一時リストの初期化
dfs = []
# 列名の設定
columns = ['subject', 'participant_id', 'condition', 'correct_c1', 'correct_c2',
           'correct_c3', 'correct_c4', 'correct_total', 'rating_t1',
           'rating_t2', 'rating_c1', 'rating_c2', 'rating_c3', 'rating_c4',
           'self_perf', 'comprehension', 'awareness', 'transcript', 'age',
           'gender', 'student', 'occupation']

# csvファイル毎に読み込み、列を整えて一時リストに追加する
for idx, study in enumerate(glob(DL_PATH)):
    # パスから研究室名を取得（フォルダ名、拡張子を削除する）
    study_name = (study.replace('./data\\', '').replace('_Data', '')
                  .replace('.csv', ''))
    # csvファイルの読み込み
    data = pd.read_csv(study, encoding='latin1', skiprows=2, header=None,
                       index_col=False).iloc[:, :22]
    # 列名の設定
    data.columns = columns
    # データを強制的に数値型に変換
    data = data.apply(pd.to_numeric, errors='coerce', axis=1)
    # 研究室ID：studyの追加
    data['study'] = idx
    # 研究室名：study_nameの追加
    data['study_name'] = study_name
    # データフレームを一時リストに格納
    dfs.append(data)

# データフレームの結合
data_merge = pd.concat(dfs, axis=0)
# 実験参加者ID：id列を追加
data_merge = data_merge.reset_index(drop=True).reset_index(drop=False)
data_merge.rename({'index': 'id'}, axis=1, inplace=True)
# 処理済みのデータフレームの表示
print('data_merge.shape:', data_merge.shape)
display(data_merge)

【実行結果】
17個のcsvファイルが統合されて、 2612行、25列のデータになりました。

続いてデータの前処理を行います。
実験にそぐわないデータ、欠損値などの処理です。
こちらもBambi ・ Exampe のサンプルコードを引用いたしました。

### データの前処理
# 引用サイト
# https://bambinos.github.io/bambi/notebooks/Strack_RRR_re_analysis.html

# 適切なデータのみ抽出：全問適切な回答、漫画を理解した、仮説等を全く意識していない
valid = data_merge.query('correct_total==4 and comprehension==1 and awareness==0')
# 漫画の面白さに欠損値があるレコードを削除
valid.dropna(subset=['rating_c1', 'rating_c2', 'rating_c3', 'rating_c4'],
             inplace=True)
# 評定値（rating）の平均値を算出・・・平均値は目的変数です
valid['mean'] = (valid[['rating_c1', 'rating_c2', 'rating_c3', 'rating_c4']]
                 .mean(axis=1))
# validの項目を限定してdataを作成
data = valid[['id', 'condition', 'study', 'study_name', 'mean']]
# 条件を整数型に変更
data = data.astype({'condition': int})
# 前処理後のデータの表示
display(data)

【実行結果】
1729名のサンプルデータとなりました。
テキストでは1796名、BambiのExampleでは1728名でした。
テキストとデータが異なることになるので、推論結果もテキストと異なることに留意しましょう。

３．データの概観の確認
テキスト表12.1の要約統計量を算出します。

### 研究室別の面白さの平均値 ※表12.1に相当

# 研究室別の参加者数の算出
num_pat = data.groupby(['study_name'])['id'].count().rename('参加者数')

## 研究室別・条件別の平均値と標準偏差の算出
tmp = data.copy()
# 実験群の参加者別の面白さの平均値から実験群全体の平均値・標準偏差を算出
tmp_experi = (tmp.query('condition==1').groupby(['study_name'])['mean']
              .agg(['count', 'mean', 'std']))
# 対照群の参加者別の面白さの平均値から対照群全体の平均値・標準偏差を算出
tmp_control = (tmp.query('condition==0').groupby(['study_name'])['mean']
               .agg(['count', 'mean', 'std']))
# データフレームを結合（参加者数・実験群の平均値等・対照群の平均値等）
stats_df1 = pd.concat([num_pat, tmp_experi, tmp_control], axis=1)
# 列名の設定（マルチインデックス）
cols1 = ['参加者数合計'] + ['実験群']*3 + ['対照群']*3
cols2 = [''] + ['参加者数', '平均', '標準偏差']*2
columns = pd.MultiIndex.from_arrays([cols1, cols2])
stats_df1.columns=columns
# インデックス名の設定
stats_df1.index.name = '研究室'
# データフレームの表示
display(stats_df1.round(2))

【実行結果】
なんとか綺麗にまとまりました！

平均値に着目します。
実験群「口を横に広げるグループ」（疑似笑顔）と対照群「口をとがらせるグループ」（笑顔では無い）の採点の平均値には差異が無いように見えます。
対照群の方が値が多い研究室もありますね。
ペンをくわえて口を横に広げても漫画の面白さがアップするわけでは無い、そんな予感がします！

モデルの構築

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\mu &\sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100,\ \text{dims}=cond)\\
\tau &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\mu_i &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\tau,\ \text{dims}=(study,\ cond))\\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper=100}) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\mu_i[stydyIdx,\ condIdx],\ \text{sigma}=\sigma) \\
\mu_{diff} &= \mu[experiment] - \mu[control] \\
\end{align*}
$$

１．モデルの定義
数式表現を実直にモデル記述します。
なお、テキストは実験群と対照群のデータを分けて取り扱っていますが、このモデルでは分けること無く、実験条件のインデックス等で識別するようにしています。

### モデルの定義

with pm.Model() as model:
    
    ### coordの定義
    # データのインデックス
    model.add_coord('data', values=data.index, mutable=True)
    # 研究室
    model.add_coord('study', values=sorted(data['study_name'].unique()),
                    mutable=True)
    # 条件
    model.add_coord('cond', values=['対照群', '実験群'], mutable=True)
    
    ### dataの定義
    # 目的変数
    y = pm.ConstantData('y', value=data['mean'].values, dims='data')
    # 研究室IDのインデックス
    studyIdx = pm.ConstantData('studyIdx', value=data['study'].values,
                               dims='data')
    # 実験条件のインデックス
    condIdx = pm.ConstantData('condIdx', value=data['condition'].values,
                              dims='data')
        
    ### 事前分布
    ## 平均μ_ijが従う正規分布のパラメータ
    # 平均μ_j
    mu = pm.Uniform('mu', lower=-100, upper=100, dims='cond')
    # 標準偏差τ
    tau = pm.Uniform('tau', lower=0, upper=100)
    ## 研究室別・実験条件別の評定値が従う正規分布のパラメータ
    # 平均μ_ij
    mui = pm.Normal('mui', mu=mu, sigma=tau, dims=('study', 'cond'))
    # 標準偏差σ
    sigma = pm.Uniform('sigma', lower=0, upper=100)
    
    ### 尤度
    likelihood = pm.Normal('likelihood', mu=mui[studyIdx, condIdx], sigma=sigma,
                           observed=y, dims='data')    
    
    ### 計算値
    muDiff = pm.Deterministic('muDiff', mu[1] - mu[0])

【モデル注釈】

  • coordの定義
    座標に名前を付けたり、その座標が取りうる値を設定できます。
    今回は次の３つを設定しました。

    • データの行の座標：名前「data」、値「行インデックス」

    • 研究室の座標：名前「study」、値「研究室名」

    • 実験条件の座標：名前「cond」、値「(対照群, 実験群)」

  • dataの定義
    次の３つを設定しました。

    • 採点の平均値：y （目的変数）

    • 研究室のインデックス：studyIdx

    • 実験条件のインデックス：condIdx（0: 対照群, 1: 実験群）

  • パラメータの事前分布

    • モデルの数式表現のとおりです。

  • 尤度

    • 平均パラメータが研究室別・実験条件別の平均$${\mu_i}$$、標準偏差パラメータが$${\sigma}$$の正規分布です。

  • 計算値

    • 実験条件別の平均$${\mu}$$を用いて、実験群全体平均と対照群全体平均の差分 muDiff を算出しています。

２．モデルの外観の確認

### モデルの表示
model

【実行結果】
シンプルなモデルだと思います。

### モデルの可視化
pm.model_to_graphviz(model)

【実行結果】
実験条件 cond 別から研究室別・実験条件別 study x cond へつながる階層構造が分かります。

３．事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　1分
# テキスト: iter=30000, warmup=5000, chains=4
with model:
    idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                      nuts_sampler='numpyro', random_seed=401)

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。

### r_hat>1.1の確認
# 設定
idata_in = idata         # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata, hdi_prob=0.95, round_to=3)

【実行結果】

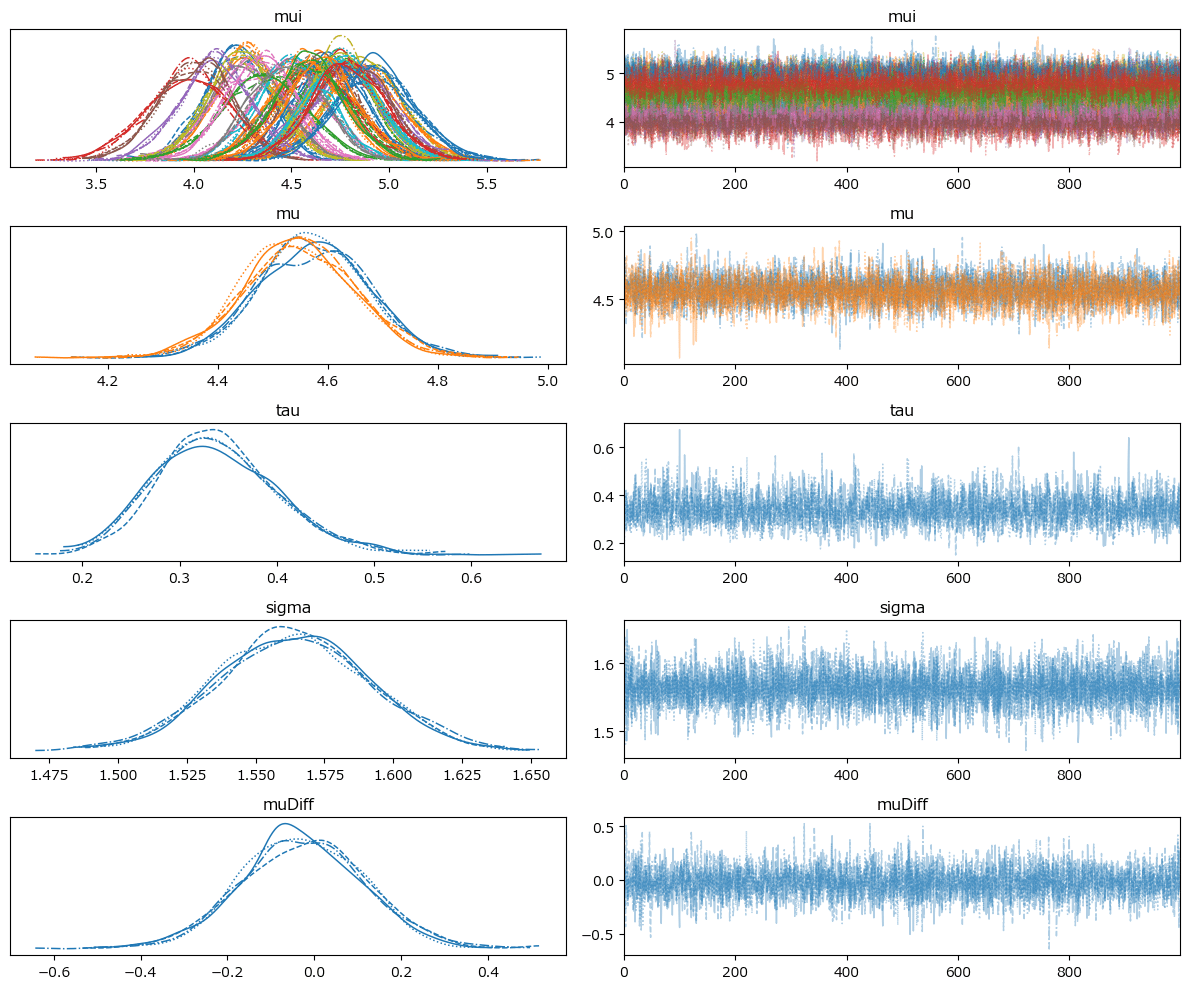
トレースプロットで事後分布サンプリングデータの様子を確認します。

### トレースプロットの表示
pm.plot_trace(idata, compact=True)
plt.tight_layout();

【実行結果】
左のグラフから、４本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

５．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata をpickleで保存します。

### idataの保存 pickle
file = r'idata_ch12.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata_ch12.pkl'
with open(file, 'rb') as f:
    idata_load = pickle.load(f)

分析～テキストにならって

１．要約統計量の確認
ひとまず pm.summary() で出力できる統計量で注目するパラメータを見ておきましょう。

### 推論データの要約統計情報の表示
var_names = ['mu', 'muDiff', 'sigma', 'tau']
pm.summary(idata, hdi_prob=0.95, var_names=var_names, kind='stats', round_to=2)

【実行結果】
なんと！疑似笑顔の実験群の平均値 mu[実験群] のほうが面白さの採点が低いではありませんか！

テキストの表12.2 階層線形モデルの推定結果表に相当する統計量を算出しましょう。

### 階層線形モデルの推定結果 ※表12.2に相当

## 事後統計量算出関数の定義
def calc_stats(x):
    ci = np.quantile(x, q=[0.025, 0.5, 0.975])
    return np.mean(x), np.std(x), ci[0], ci[1], ci[2]

## 事後統計量の算出
stats_df2 = pd.DataFrame({
    '実験群': (calc_stats(idata.posterior.mu[:, :, 1]
                         .stack(sample=('chain', 'draw')).data)),
    '対照群': (calc_stats(idata.posterior.mu[:, :, 0]
                         .stack(sample=('chain', 'draw')).data)),
    '実－対': (calc_stats(idata.posterior.muDiff
                         .stack(sample=('chain', 'draw')).data)),
    'σ': calc_stats(idata.posterior.sigma.stack(sample=('chain', 'draw')).data),
    'τ': calc_stats(idata.posterior.tau.stack(sample=('chain', 'draw')).data)},
                         index=['EAP', 'SD', '2.5%CI', 'MED', '97.5%CI']).T
display(stats_df2.round(2))

【実行結果】
テキストの結果と比べると実験群不利（？）な結果です。
大まかにはテキストの結果と近しいのでは無いでしょうか。

【考察】
採点の差「実－対」はほぼゼロであり、95%信用区間が0を含んでいます。
実験群と対照群の差は現実的に意味のある差とは言えないだろう、とするテキストの考察に賛成です。

２．採点の平均に関する実験群と対照群の差
採点の平均に関して実験群が対照群を上回る確率をPHC曲線の形式で可視化します。
テキストの図12.2に相当します。

### μ実－μ対＞cのPHC曲線の描画 ※図12.2に相当

## phcの算出
# 推論データからμ実－μ対データを取り出し
mu_diff = idata.posterior.muDiff.stack(sample=('chain', 'draw')).data
# cの区間の設定
cs = np.linspace(-0.5, 0.5, 1001)
# μ実－μ対＞cの確率（割合）の算出
phc = [np.mean(mu_diff > c) for c in cs]

## 描画
plt.figure(figsize=(7, 3))
# PHC曲線の描画
plt.plot(cs, phc)
# 修飾
plt.xlabel('c')
plt.ylabel('研究仮説が正しい確率：得点差>c')
plt.grid(lw=0.5);

【実行結果】

合わせて採点差が0を超えるという研究仮説が正しい確率を算出します。

print(f'μ実－μ対＞0の確率: {np.mean(mu_diff > 0):.2f}')

【実行結果】
43% です。
この記事の結果は「実験群の方が面白い感じた割合が半数未満」ということになりました。
なおテキストは 53% です。

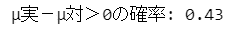
テキスト図12.3の採点差の絶対値に関するPHC曲線を描画します。

### |μ実－μ対|＜cのPHC曲線の描画 ※図12.3に相当

## phcの算出
# cの区間の設定
cs2 = np.linspace(0, 0.5, 1001)
# |μ実－μ対|＜cの確率（割合）の算出
phc2 = [np.mean(abs(mu_diff) < c) for c in cs2]

## 描画
plt.figure(figsize=(7, 3))
# PHC曲線の描画
plt.plot(cs2, phc2)
# 修飾
plt.xlabel('C')
plt.ylabel('研究仮説が正しい確率:\n得点差の絶対値<c')
plt.grid(lw=0.5);

【実行結果】

【考察】
実験群の方が採点が大きい（採点差が０を超える）確率 43% を鑑みると、実験群の採点は対照群よりも高いとする研究仮説が正しいとは言えない感じがいたします。

３．研究室ごとの要約統計量の算出
テキスト表12.3の各研究室ごとの差得点、非重複度、優越率を算出します。
MAPに代えて事後平均（EAP）を用いています。

### 研究室ごとの差得点、非重複度、優越率の算出 ※表12.3に相当

# 推論データからμ実、μ対、標準偏差の事後分布サンプリングデータを取り出し
mu_exper = idata.posterior.mui[:, :, :, 1].stack(sample=('chain', 'draw')).data
mu_contr = idata.posterior.mui[:, :, :, 0].stack(sample=('chain', 'draw')).data
sd = idata.posterior.sigma.stack(sample=('chain', 'draw')).data

# 統計量を格納するデータフレームの初期化
stats_df3 = pd.DataFrame()
# 研究所名の配列の作成
studys = sorted(data['study_name'].unique())
# 研究所ごとに統計量算出を繰り返し処理
for i in range(len(studys)):
    # 研究所名の取得※
    name = studys[i]
    # μ実－μ対の取得
    diff = mu_exper[i, :] - mu_contr[i, :]
    # μ実－μ対の平均の算出※
    es = np.mean(diff)
    # μ実－μ対の標準偏差の算出※
    sdd = np.std(diff)
    # μ実－μ対＞0の平均の算出※
    es_over = np.mean(diff > 0)
    # 非重複度の算出※
    u3 = np.mean(stats.norm.cdf(x=mu_exper[i, :], loc=mu_contr[i, :], scale=sd))
    # 優越率の算出※
    pi = np.mean(stats.norm.cdf(x=(diff / sd)/np.sqrt(2), loc=0, scale=1))
    # 算出した統計量を一時データフレームに格納　※印の変数をデータフレーム化
    tmp_df = pd.DataFrame({name: [es, sdd, es_over, u3, pi]}).T
    # 統計量を格納するデータフレームに結合
    stats_df3 = pd.concat([stats_df3, tmp_df], axis=0)
# データフレームの列名の設定
stats_df3.columns = ['μ実－μ対（EAP）', 'SD', 'μ実－μ対＞0', '非重複度', '優越率']
stats_df3.index.name = '研究室'
# データフレームの表示
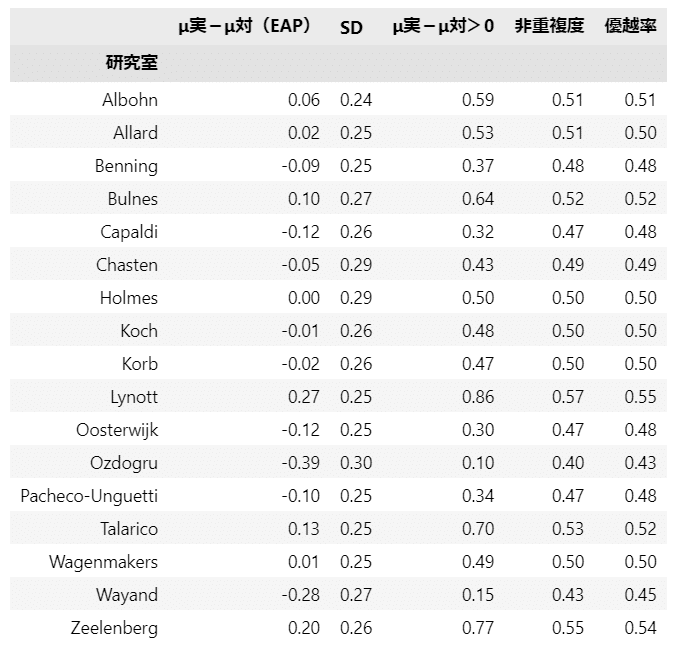
display(stats_df3.round(2))

【実行結果】
テキストの結果と近い感じでしょうか。

【考察】
実験群の方が採点の平均値が高い結果となった研究室は８です（テキストは９）。
最も平均値差の大きいのは Lynott 研究室の 0.27 （テキストは 0.29）ですが、1988年論文研究の差は 0.82 なので、0.27 という値は大きいとは言えないようです。
また、Lynott 研究室の実験群の採点が対照群を上回る確率は 0.86 （テキストは 0.88）。
テキストによると 95% あるいは 97.5% 基準が統計学の常用とのことなので、88% は基準に到達していないことになります。

まとめ的には、追試結果に基づくベイズ推論結果は、1988年研究の結果を再現できたとはいいがたい、ようです。
なお、テキストは「今回の結果で表情のフィードバック効果仮説が間違いだったと結論づけるのは早計である」と警鐘しています。

おまけ

Bambi でモデルを作ってみましょう。
ここでは単純モデルを構築します。
コードと実行結果を淡々と記載しますのであしからず。

１．準備

### 追加インポート
import bambi as bmb
### データの前処理
# 引用サイト
# https://bambinos.github.io/bambi/notebooks/Strack_RRR_re_analysis.html

# 適切なデータのみ抽出：全問適切な回答、漫画を理解している、仮説等を全く意識していない
valid = data_merge.query('correct_total==4 and comprehension==1 and awareness==0')
# 漫画の面白さに欠損値があるレコードを削除
valid.dropna(subset=['rating_c1', 'rating_c2', 'rating_c3', 'rating_c4'],
             inplace=True)
# validの項目を限定してdataを作成
data2 = pd.melt(valid, ['id', 'condition', 'gender', 'age', 'study', 'self_perf'],
               ['rating_c1', 'rating_c2', 'rating_c3', 'rating_c4'],
               var_name='stimulus')
# 前処理後のデータの表示
display(data2)

【実行結果】

２．モデルの構築

### モデルの定義
model_bmb1 = bmb.Model(
    formula='value ~ 1 + condition + (1 | id) + (1 + condition | study)',
    data=data2,
    dropna=True
)
### モデルの表示
print(model_bmb1)

【実行結果】

### モデルの可視化
model_bmb1.build()
model_bmb1.graph()

【実行結果】

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　1分30秒
# テキスト: iter=30000, warmup=5000, chains=4
idata_bmb1 = model_bmb1.fit(draws=1000, tune=1000, chains=4, target_accept=0.8,
                            nuts_sampler='numpyro', random_seed=401)

【実行結果】省略

３．収束確認

### r_hat>1.1の確認
# 設定
idata_in = idata_bmb1    # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】収束しました。

### トレースプロットの表示 3分
pm.plot_trace(idata_bmb1, compact=True)
plt.tight_layout();

【実行結果】

４．要約統計量（テキスト表12.2相当）

### bambiモデルの推定結果 ※表12.2に相当

## 全体切片Interceptと実験条件切片conditionで算出(研究室・被験者個人の効果を排除)
# 実験群
exprmt = ( idata_bmb1.posterior.Intercept.stack(sample=('chain', 'draw')).data
          + idata_bmb1.posterior.condition.stack(sample=('chain', 'draw')).data)
# 対照群
contrl = idata_bmb1.posterior.Intercept.stack(sample=('chain', 'draw')).data

## 統計量の算出
stats_df4 = pd.DataFrame({
    '実験群': (calc_stats(exprmt)),
    '対照群': (calc_stats(contrl)),
    '実－対': (calc_stats(exprmt - contrl)),},
                         index=['EAP', 'SD', '2.5%CI', 'MED', '97.5%CI']).T
display(stats_df4.round(2))

【実行結果】

先程の Bambi Example のサイトにはもっと複雑でデータに適したモデル例がありますので、ぜひお試しくださいね！

以上で第12章は終了です。

おわりに

研究論文

学問の世界の研究論文、とても敷居の高いワードです。
日常生活では決して目にすることがない高嶺の花、異世界の恋文。
たのしいベイズモデリングの執筆者の方々はかの学術界の人々。
なんだか恐れ多い感じがいたします。
でも、たのしいベイズモデリングでキャッチーなテーマを扱ってくださり、ベイズやデータ分析の楽しみ方を教えてくださるフレンドリーな先輩、のような気もいたしております。

おわり

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

いいなと思ったら応援しよう！

この記事が参加している募集

#新生活をたのしく

47,020件

#うちの積読を紹介する

2,210件