材料力学から始まる変形理論 -1-

静岡の絶景を楽しめる日本一長い吊り橋「三島スカイウォーク」の写真です。富士山を望む眺めはまさに絶景の一言です。

三島スカイウォークは2017年にグッドデザイン賞（ビジネスモデルと土木構造物の2部門）を受賞していて、秀逸な構造物としても知られています。

このような構造物はデザイン性はもちろんですが、何より十分な耐久性を有している必要があります。一度でも崩壊するれば大事故につながりますし、人命に関わることも想定されるためです。

安全性を満たした構造物を設計するには、相応の知識が必要になります。そのひとつが「材料力学」です。今回は数回に分けて、材料力学すなわち物体の変形理論について書くことにします。

材料力学は個人的にも好きな学問のひとつで、現在の仕事の基礎にもなるので、その辺の話にも触れていこうと思います。最後までお付き合い頂けたら幸いです。

材料力学について

機械工学系の大学（学部）に進学した際の必修科目として、通称「4力学」と呼ばれる科目があります。主に機械力学・熱力学・流体力学・材料力学を指しますが、中でも物体の変形理論を扱うのが材料力学です。

物体に何かしらの力が作用すると、物体は「変形」を引き起こします。ここで言う変形は「物体の形状が変化すること」を意味します。それは目視では気付かない微小変形から明らかな大変形まで様々です。

材料力学は物体がどの程度変形するか（最終的には壊れないか）を定量的に評価するための学問です。

材料力学を現実の目的に置き換えると、軽くて丈夫な構造物を造ることが挙げられます。冒頭で紹介した三島スカイウォーク（吊り橋）もそうですが、コストを押えた範囲で耐久性を確保することが求められます。

例えば、立橋などは一般的に「H鋼」と呼ばれる構造部材が使われます。材料力学の用語で断面係数という定数がありますが、H鋼は断面係数を高くできる（曲げ変形に強い）という特徴があります。

コストを押えて強度（耐久性）は高くという要求は年々増してきています。材料力学はこのような要求に応えるために必要な学問なのです。

変形の基本形態

微小変形から大変形まで、程度こそ違えど多くの場面で観察される変形ですが、その挙動はシンプルに5つに分けられます。

引張・圧縮・せん断・曲げ・ねじりの5つです。ポイントは、現実に発生する変形はこの5つの挙動を複合したものであるということです。

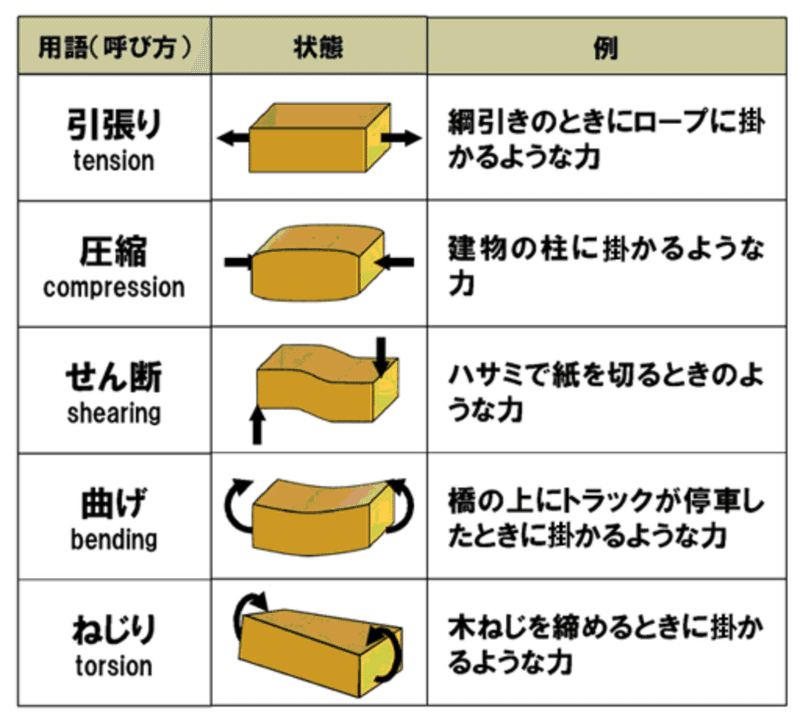
引張・圧縮・せん断は基本的な挙動であり、垂直力やせん断力と表記される時もあります。一方で、曲げは垂直力（引張と圧縮）が不均一に発生し、ねじりはせん断力が不均一に発生することが知られています。

変形と内力の考え方

材料力学は4力学の中でも高校物理に類似した科目であり、進学して早々に学習する方が多いと思います。

例えば、高校物理は力と言うと「外力」を指すことが多く、物体内部に発生する力という表現には慣れていません。力のつり合いを考えるときに、作用・反作用の法則を持ち出すことがあります。

材料力学では、外力が作用すると物体内部には外力に抵抗する力が生じると考えます。この外力に抵抗する力のことを「内力」と言います。

外力が作用しても、物体は何も変化が無いように見えます。これは外力と内力が釣り合うからです。仮に内力が発生しないとすると、物体は抗力なしに自由に変形することになります。

材料力学では、この内力のことを総称した「応力」と言います。また、物体の変形の程度を表す指標として「ひずみ」と呼ばれる物理量があります。このふたつは材料力学で最も登場する言葉です。

おわりに

今回から「材料力学」に関する話を書いていきます。初回となる今回は材料力学がどういう学問なのかなどを書きました。

材料力学は目視で現象を確認する機会が多い科目でもあります。理論的な話は数学が物理が絡んできますが、なるべく数式ではなくて物理的な背景（意味）を中心に話を進めていきます。

次回は簡単な単軸引張（圧縮）を例にして、変形という概念を深掘りしたいと思います。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎