解析学（微分積分）の深掘り 〜２〜

数学の中でも「解析学」は個人的に使用頻度が高い内容でした。解析学とは「微分積分」を軸とする計算の分野です。今回はそんな微分積分について、様々な視点から書いていくシリーズです。

前回は微分積分とは何かについて書きました。

今回は微分積分を使うことで明らかになることの一例として、球や円すいの体積を求める公式の導出をしてみたいと思います。

前提となる計算方法

下記の方法を用います。右側にあるグラフｙ（変数ｘの関数）と区間（ａーｂ）で囲まれた領域を回転させることで作られる立体を想定します。

回転体なので、位置ｘで縦に切り出した断面の形状は円です。つまり、断面積はグラフｙの値を半径とみなして計算することができます。

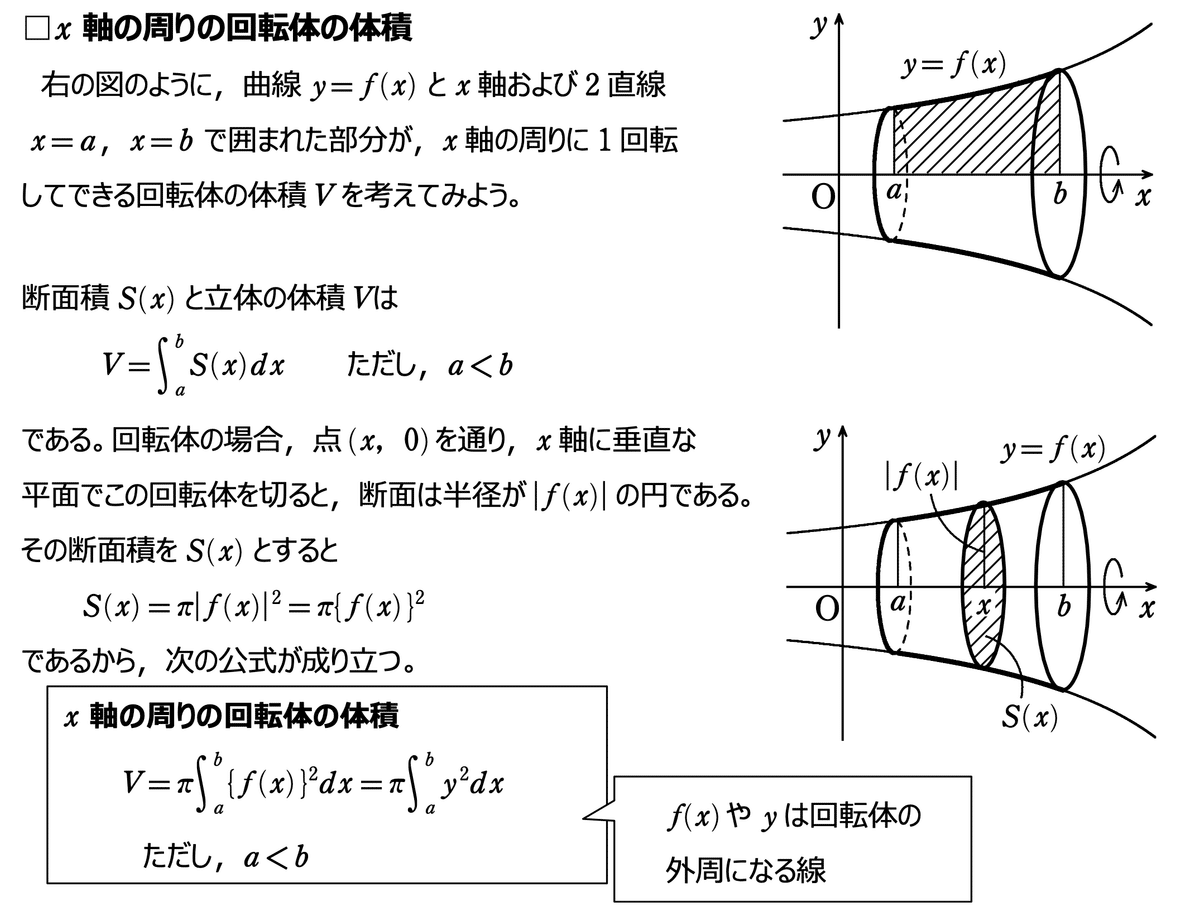
以上の考え方に基づいて、回転体の体積を定積分で求めます。何を回転させることで球や円すいになるかを考えることが、ひとつのポイントです。

球の体積の公式を導出する

平面図形（円）を軸まわりに回転させることで球は完成します。円の方程式は高校で学習する内容です。そこから定積分の形に落とし込みます。

円すいの体積の公式を導出する

下記の１次関数の方程式（グラフ）を軸まわりに回転させることで、円すいは完成します。ここで、１次関数の方程式（グラフ）は円すいの稜線に相当します。そこから定積分に落とし込みます。

おわりに

今回は微分積分が何に使えるのかを知るために、既に学習した立体図形の体積の公式を導き出してみました。こうして見ると、より微分積分を身近に感じてもらえるかと思います。

まずは微分積分の表面的な理解に留めましたが、ここから解析学の現代の使い道について、より深掘りしていきたいと思います。

-------------------------

最後まで読んでいただき、ありがとうございます。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに寄り添えたら幸いです。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ プロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎