【#17】材料力学の強化書 〜曲げ応力と曲げモーメントについて〜

今回のトップ画像はイギリスはスコットランドにあるエディンバラ城です。その城下町は中世の街並みを再現していて、有数の観光地として知られています。

１２世紀から１６世紀までの間の数多くの戦争で、破壊されては再建されることを繰り返してきたそう。なかなかの苦労を感じさせますね。

さて、材料力学の話に戻りましょう。

前回は微分積分の応用として「微分方程式」について説明しました。今後の単元として「曲げ」という変形を扱う上で必要になるので、頭の片隅に置いておくと良いと思います。

今回から「曲げ」について説明していきます。まずは計算問題に入る前に、曲げという変形に関する用語をいくつか説明します。今回はタイトルに示した通り、曲げ応力と曲げモーメントについて見ていきます。

曲げ変形に関する仮定

下記の図のように支柱に支えられた棒に重りを載せたとき、棒は「曲げ」の変形を生じます。厳密にはこの変形は「たわみ」と呼ばれています。

このとき、棒がたわむことに対する抵抗として、棒の内部に応力が発生します。この内部に発生する垂直応力のことを「曲げ応力」と言います。

ここから、曲げ応力の計算方法に触れていきます。その上で、はりの横断面は変形後も平面を保ち、軸線に直交すると仮定します。この仮定は「ベルヌーイ・オイラーの仮定」と呼ばれており、はりが均質な材料で構成されて大きなたわみを生じない場合に成立します。

曲げ変形を分解してみる

曲げ応力は引張応力と圧縮応力が不均一に作用することで発生します。実際に曲げの状態を想定しながら考えると分かりやすいです。

特に、曲げにおいては引張りも圧縮も生じない曲面が存在します。この曲面のことを「中立面」と言います。その中立面から見て、凹側は圧縮変形が、凸側は引張変形が生じます。

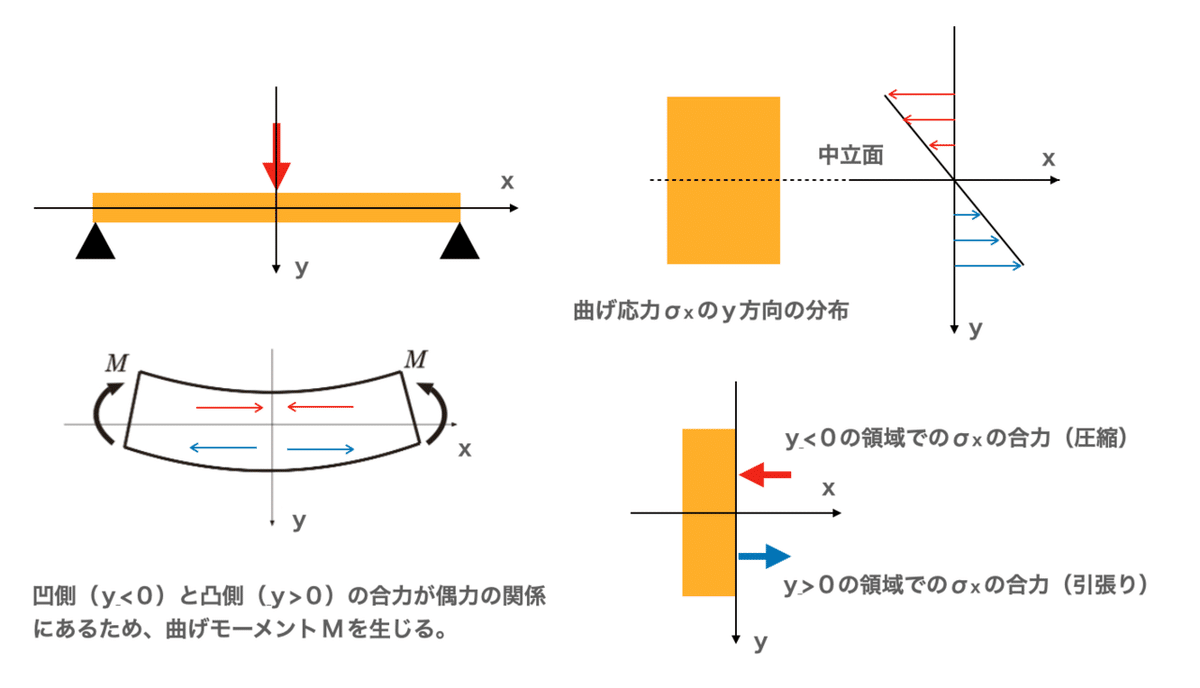
この２種類の変形力が偶力の関係にあることから、曲げモーメント（Ｍ）を生じることになります。なお、部材に軸力は生じないので、２種類の変形力は大きさとしては同じです。

または、曲げモーメントは「横断面の中立軸まわりのモーメント」と理解するでも良いです。中立軸は横断面の図心を通る軸のことです。

曲げ応力と曲げモーメントの関係式

曲げ応力（σx）とモーメント（M）の関係式はこちらになります。

$${{\sigma}_x={\frac{M}{I_z}}y}$$

ここで、$${I_z}$$は中立軸に関する断面二次モーメントであり、横断面の形状に依存する定数です。

曲げ応力は凹側と凸側で正負が逆転します（右辺の座標ｙで対応します）。つまり、曲げ応力が最も大きくなるのは、部材表面であることが分かります。

また、断面二次モーメントは部材の曲げにくさ（曲げに対する抵抗性）を表しており、この値が大きいほど曲げ応力は小さくなります。

曲げ応力（σx）とモーメント（M）の関係式の導出はこちら。ぜひ参考にしてみてください。

おわりに

今回から曲げの変形について扱い始めましたが、用語が色々と出てきて大変かと思います。まずは、曲げが生じた時のイメージと引張力と圧縮力をつなげて理解して頂ければと思います。

曲げ応力と曲げモーメントの関係式で出てきた「断面二次モーメント」は材料力学の書籍を調べれば出てきますが、実際に算出する過程も知れた方が良いので、次回で説明します。

-------------------------

最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに添えるように頑張ります。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎