【#34】材料力学の強化書 〜モールの応力円について〜

今回のトップ画像は、皆さんもよくご存知のピサの斜塔です。イタリアのトスカーナ州ピサ市にある建物で、具体的にはピサ大聖堂の鐘楼を指します。世界遺産「ピサのドゥオモ広場」を構成する建築物の一部で、ここは洗礼堂、大聖堂、鐘楼、墓所回廊の４つで構成されているそうです。

さて、材料力学の話に戻りましょう。

前回から新章に入りました。前回は変形に関する分析で重要な「主応力」について説明しました。

物体がある応力状態を示しているとき、座標軸を回転させることで応力成分が擬似的に変化します。ここで、せん断応力成分がゼロになる時の垂直応力のことを「主応力」と呼びました。

前回は図的に解説していきましたが、今回は２次元の応力状態で使えるツールひとつ「モールの応力円」について扱います。やり方を知ればすぐ使える方法でもあるので、覚えて損はないかと思います。

モールの応力円の概要

下記のノートに整理しました。前回の２次元の応力状態を表した２式を変形したものになります。式（ｃ）が整理した式なのですが、見ての通り円の方程式に対応していることが分かります。

主応力と最大せん断応力はモールの応力円のどこに対応するかについても、触れておきます。

主応力は座標変換（座標軸を回転移動させること）により、せん断応力成分がゼロになる場合を指すので、横軸と交点をつくる位置が主応力になります。

最大せん断応力は円の中心（横軸の位置は２つの垂直応力の平均値）から、縦軸を引いて円と交点を結ぶ位置になります。

モールの応力円に関する例題

例題として、２次元である瞬間の応力状態が既知であるときの主応力と主軸方向について求めてみます。

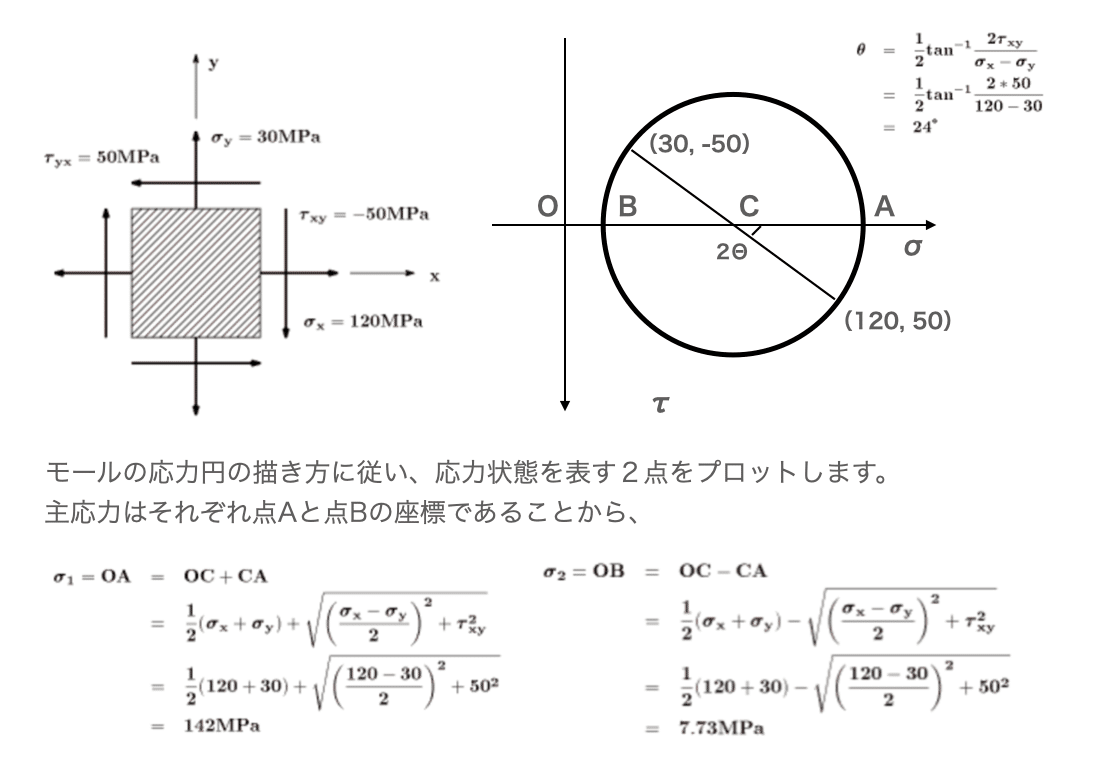
まずはモールの応力円の描き方に従い、与えられている応力状態についてプロットします。そこから、横軸（垂直応力）の交点Ｃを求めて、円を描きます。

また、主軸方向（主応力方向）については、前回で整理した式から求めます。最大せん断応力については各自で求めてみましょう（円の縦軸方向の最大値を円の性質から求めれば良いです）。

最後に重要な性質を書いておきます。応力状態は座標軸の変換で擬似的に変化しますが、主応力や最大せん断応力は座標変換に依存しない固有の値を持ちます（座標系に依存しないということです）。

この性質は今後も重要になるので、確実に理解しておきましょう。

おわりに

今回は２次元の主応力を簡単に求めるためのツールとして、モールの応力円について紹介しました。円の方程式については高校レベルの数学の問題なので、そこから復習していくと確実だと思います。

次回は３次元の応力状態に拡張してみたいのですが、固有値問題に持ち込む必要があるので、その辺の復習も交えて説明していきたいと思います。

-------------------------

最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに添えるように頑張ります。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎