解析学の基礎である微積分の話 -3-

前回に引き続き「解析学」をテーマに書きます。解析学は数学を構成する大きな分野のひとつで、高校数学で学習する「微積分」を本格的に紐解いたものです。

前回は基本の話として積分について取り上げました。

今回は解析学の中でも実用的に使う頻度が多い「微分方程式」についてです。物理的な事象を定式化する際にはほぼ確実に登場する単元であり、簡単なところでも使える話なので、お付き合いいただけたら幸いです。

微分方程式とは

微分方程式は数学で言う方程式のひとつです。１次方程式や２次方程式は中学校で見聞きしていますが、方程式なので「解」が存在するという点は同じです。

微分方程式は解となる変数（関数）の微分形式が登場する方程式です。これまでの方程式との違いは、解が定数ではなく変数（関数）で表現されることです。

例えば、独立変数（x）と従属変数（y）による常微分方程式を解いてみます（微分方程式の解が１変数関数である場合を「常微分方程式」と呼びます）。

exp(※)は自然対数の底（ネイピア数）の指数関数を表す数学記号です。(※)が指数の肩に当たります。

ポイントのひとつは不定積分を扱うことで、不定積分には積分定数が必要です。これは解の従属変数（y）を微分すると、定数項はゼロになることに由来します。

この積分定数が含まれる状態の解は「一般解」と呼ばれます。数値条件を与えることで積分定数は一意に求まりますので、それを加味した状態の解は「特殊解」と呼ばれます。

微分方程式の用途

先ほど、微分方程式は物理的な事象を定式化する際にはほぼ確実に登場する単元と書きました。その理由のひとつは、物体の運動を求める出発点の「運動方程式」が時刻（t）による微分方程式で記述されるためです。

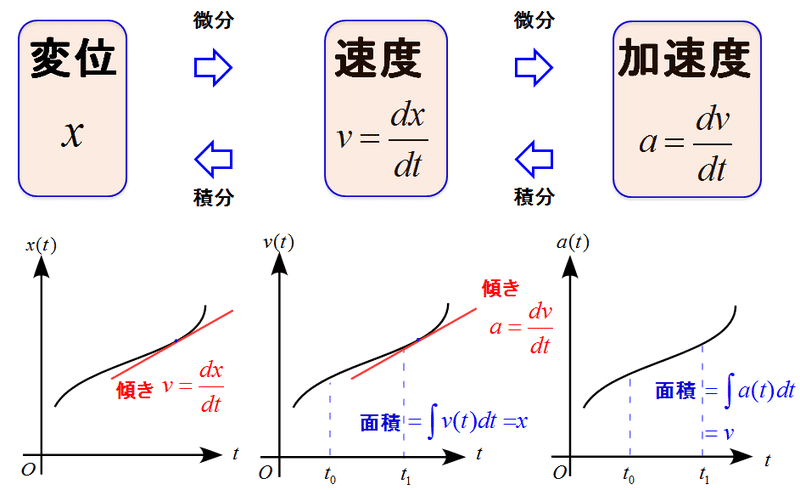
つまり運動方程式から物体の運動を求める作業とは、微分方程式を解く作業であることに他なりません。

実際に加速度が定数（a）の「等加速度直線運動」について考えてみます。

加速度を時刻（t）で積分すると速度の関数（v）が求まります。初速度の条件を付与すると、速度（v）の特殊解が現れます。そこからもう一度時刻（t）で積分すると変位（x）が求まります。

こうして変位（x）を時刻（t）の関数として求めましたが、これは高校物理で習う等加速度直線運動の公式であることが分かります。

おわりに

今回は解析学の本場とも言える「微分方程式」の話を書きました。

簡単な微分方程式の例題から、物理（高校物理）の公式の過程を導き出した訳ですが、このことからも、微分方程式の理解は数学に留まらないレベルで重要だということが分かると思います。

今回は１変数関数の常微分方程式を扱いましたが、多変数関数を扱う「偏微分方程式」もあり、これは相当なテクニックを使う単元です。機会があれば話をしようと思います。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎