
【#09】材料力学の強化書 〜熱応力について〜
今回のトップ画像は、みなとみらいにある横浜美術館です。夜景に応じて柱が光を出していて綺麗です。たくさんの大切な展示物がある訳ですから、きちんとした耐久性を持ち合わせてないといけません。
さて、材料力学の話に戻りましょう。
前回は不静定問題について扱いました。静力学的な力のつり合い条件と変形条件を組み合わせて解いていくんでしたね。
今回は熱応力について扱います。物体は温度変化にさらされると伸びたり縮んだりします。そして、物体の伸縮が妨げられると、そこに応力が発生します。その計算の流れについて見ていきましょう。
![]()
熱応力とは
下記のように物体の両端を固定して、熱(温度変化)による自由な変形が発生しないようします。すると、本来の変形を打ち消すような外力(P)と同じ効果を物体に与えることになり、物体に応力が発生します。
この応力のことを「熱応力」と言います。
熱応力は部分的に拘束された状態で、温度変化が存在するならば、どのような物体でも発生します。そして、その量は物体の材質に依存します。
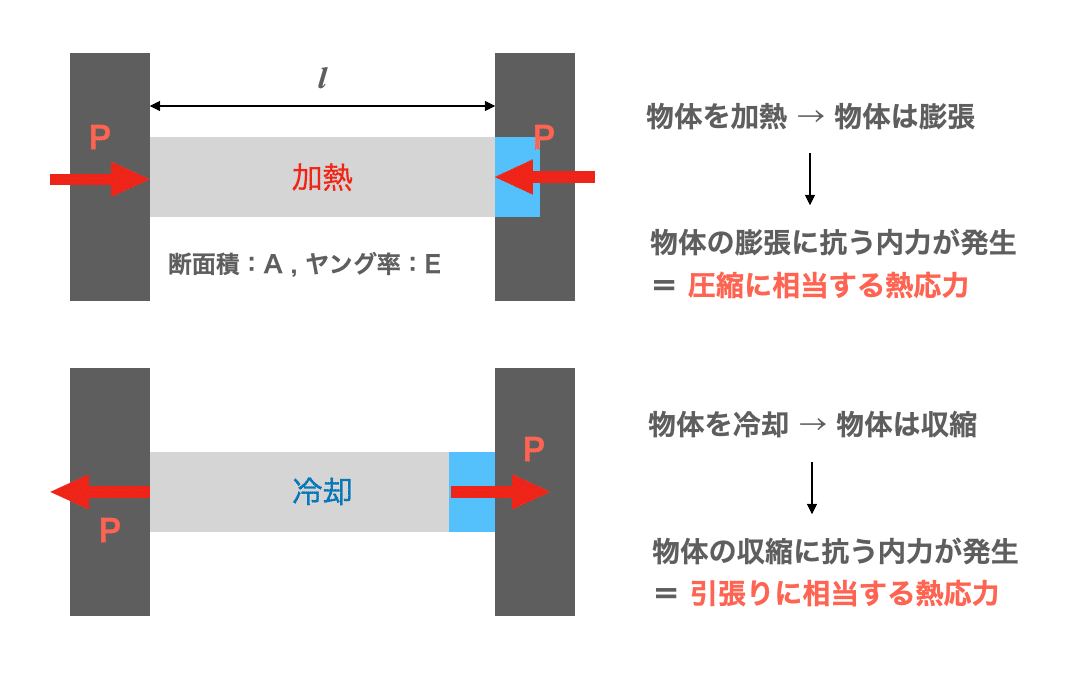
図に示したように、物体が加熱された場合は、物体の膨張を妨げるような圧縮力が内力として発生します(圧縮応力に相当)。逆に、物体が冷却された場合は、物体の収縮を妨げるような引張力が内力が発生します(引張応力に相当)。
![]()
熱応力の計算方法について
実際に熱応力を計算する流れを見ていきます。
物体が加熱されたとき、実際は両端が拘束されていることで、圧縮する方向に内力が発生します。その際の変形量を仮定します。圧縮であることを考慮すると、仮想的な変形量(λ)は次の通りになります。
$${\lambda=-\frac{Pl}{AE}}$$
この仮想的な変形量と自由熱膨張量の和はゼロになります。また、ここで出てきた自由熱膨張量とは、線膨張係数(α)と温度変化量(ΔT)と棒の全長を掛けた値として定義されます。
$${{\lambda}_T={\alpha}{\Delta}Tl}$$
全体の変形量はゼロであることを利用して、仮想的な外力(P)を求めます。
$${{\lambda}+{\lambda}_T=0}$$ → $${P=AE{\alpha}{\Delta}T}$$
そして、熱応力の計算については、今回は圧縮方向に作用することを考慮して、次のように求められます。
$${\sigma=-\frac{P}{A}=-E{\alpha}{\Delta}T}$$
以上が熱応力を計算する流れになります。注意したいのは、温度変化で物体が膨張した時は熱応力は符号がマイナス(圧縮力が作用するため)、物体が収縮した時は熱応力は符号がプラス(引張力が作用するため)になる点です。
分からなくなった時は、熱応力の発生の過程を思い出しながら、きちんと判断して頂けたらと思います。
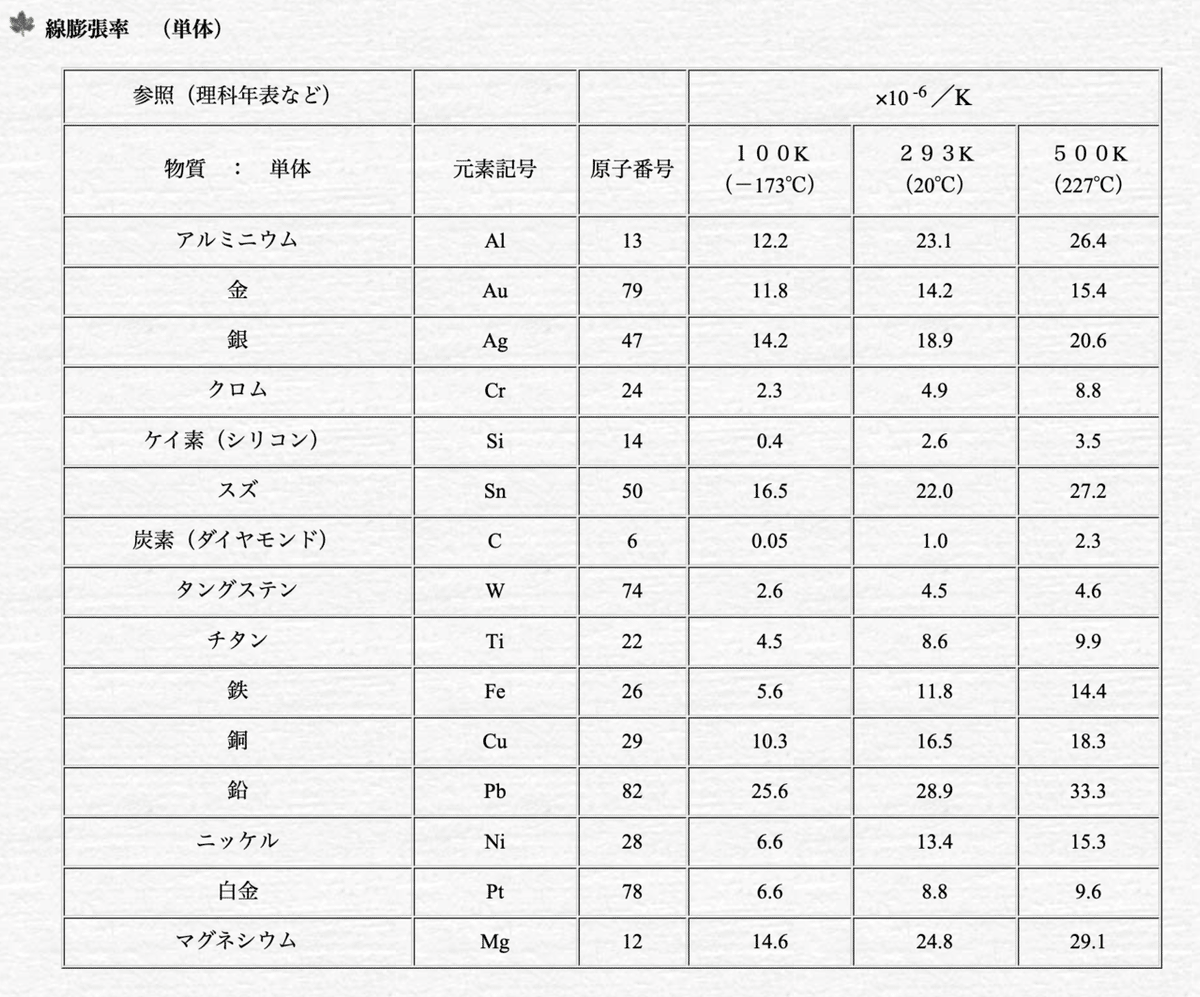
■参考:物質(単体)の線膨張係数
![]()
体膨張率について
線膨張係数(α)を3次元に拡張した定数のことを体膨張率(β)と言います。両者の関係を見ていきます。
一辺の長さ(l)の立方体に、温度変化(ΔT)によって下記のように体積変化が生じたとします。
$${{\Delta}V={\beta}{\Delta}T{l^3}}$$
一辺の長さの変化量は線膨張係数(α)を用いて表せますので、体積の変化量は次のようになります。
$${{\Delta}V={\beta}{\Delta}T{l^3}=(1+{\alpha}{\Delta}T)^3{l^3}-{l^3}=[3{\alpha}{\Delta}T+3({\alpha}{\Delta}T)^2+({\alpha}{\Delta}T)^3]l^3}$$
ここで「αΔT」の値が十分に小さいとすると、大括弧内の2項目と3項目は無視できます。以上より、線膨張係数(α)と体膨張率(β)は次の関係になります。
$${{\alpha}=\frac{\beta}{3}}$$
体膨張率も重要な定数のひとつなので、一緒に押さえておきましょう。
![]()
演習問題を解いてみる
最後に1問だけ演習問題を解いてみます。3本の棒を組み合わせた構造体が熱膨張する場合の全体の変形量を求める問題です。

流れは先ほどの話を基にしていますが、式展開が少し複雑になるので、ひとつひとつを着実に追うようにしていただければ良いです(前回の不静定問題でも同じことを言いましたね)。
![]()
おわりに
今回は熱応力について、実際に演習問題を交えて説明しました。
実用レベルで熱応力を考慮しなければならないのは、異なる線膨張係数の材料を組み合わせて使う場合です。
先ほども触れましたが、線膨張係数は材質ごとに固有の値を持ちます。これを考慮しなければ、温度変化の際に構造物が破損するという事態になりかねません。
実用レベルで必要となる知識のひとつなので、きちんと押さえて頂けたらと思います。
-------------------------
最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな1ページに添えるように頑張ります。何卒よろしくお願いいたします。
-------------------------
⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎
⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎
