【#40】材料力学の強化書 〜カスティリアノの定理（１）〜

今回のトップ画像は重要伝統的建造物群として知られます、御手洗の常盤町通りの風景です。広島県呉市の安芸灘（あきなだ）に浮かぶ大崎下島の小さな港町で、江戸時代以降に発展したとのこと。

江戸時代の面影を色濃く残しており、まるで時間が止まっているかのようです。ぜひ現地でその雰囲気を味わいたいですね。

さて、材料力学の話に戻りましょう。

前回はねじりや曲げにおけるひずみエネルギーについて考えました。材料力学で扱う多種多様な変形に対するひずみエネルギーの定式化を整理しました。

今回はひずみエネルギーを応用したはりのたわみの計算について見ていきます。カスティリアノの定理と呼ばれる手法です。外力のなす仕事の変化はひずみエネルギーの変化に対応することが基本的な考え方です。

カスティリアノの定理

外力のなす仕事とエネルギーの関係は弾性体においても成立します。そこで、複数の荷重が作用する場合について考えてみます。

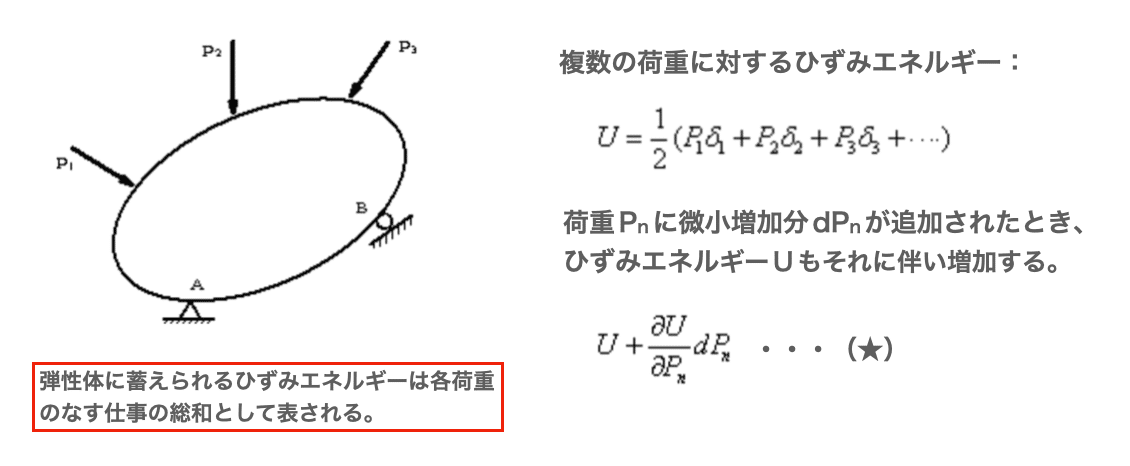
複数の荷重に対するひずみエネルギーは、単純に各々の仕事を総和することで求まります。そこに微小荷重が追加されると、それに伴いひずみエネルギーも増加することが分かります（★で示した数式に対応）。

今度は最初に微小荷重（dPn）を加えて、P1･P2･P3…の順に作用させてみます。

この時のひずみエネルギーの総和は（★）で示した式に等しくなるので、次のようになります。

$${U+\frac{\partial U}{\partial P_n}dP_n=U+dP_n\delta_n}$$

 この式を整理すると、次のようになります。

$${\delta_n=\frac{\partial U}{\partial P_n}}$$

ここで「$${\partial}$$」は偏微分を表します。多変数関数において特定の変数に対して微分する、という意味として捉えてください。

上記の式は、複数ある荷重（群）の中から特定の荷重でひずみエネルギーを偏微分すると、その荷重の作用点における作用方向の変位を求めることができる、ということを示しています。

このことを「カスティリアの定理」と言います。はりやトラスの問題では、集中荷重が作用する場合にカスティリアノの定理を利用して、集中荷重の作用点におけるたわみを求めることができます。

基本的な例題

カスティリアノの定理を用いてはりのたわみを求めるまでの流れを見てみます。今回は片持ちはりで先端に集中荷重が作用する場合と、分布荷重が作用する場合について扱うことにします。

それぞれ過去に扱ったことのある例題ですが、特に集中荷重が作用する場合においてはたわみの方程式を介さずに求めることができるので、計算過程は多少楽になるはずです。

分布荷重の場合は少し考え方が複雑です。集中荷重が存在しないため、仮想的な集中荷重を設けて、それを考慮したひずみエネルギーを求めます（最終的に集中荷重をゼロにして答えを導きます）。

おわりに

今回はひずみエネルギーの応用編として、カスティリアノの定理とそれを利用したはりのたわみの求め方を見ていきました。

偏微分が初めて登場するので、聞き慣れないところもあるかと思いますが、少しずつ理解を進めて頂ければと思います。

-------------------------

最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな１ページに添えるように頑張ります。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎