アインシュタインタイルでボードゲームの盤面をつくる。とにかく遊んでみる。
前回の記事はこちら。
せまゲーとアインシュタインタイルをいったりきたりしております。
今回は、アインシュタインタイル(代表して、HAT)とボードゲームの合体でいきます。
手頃なサイズ感
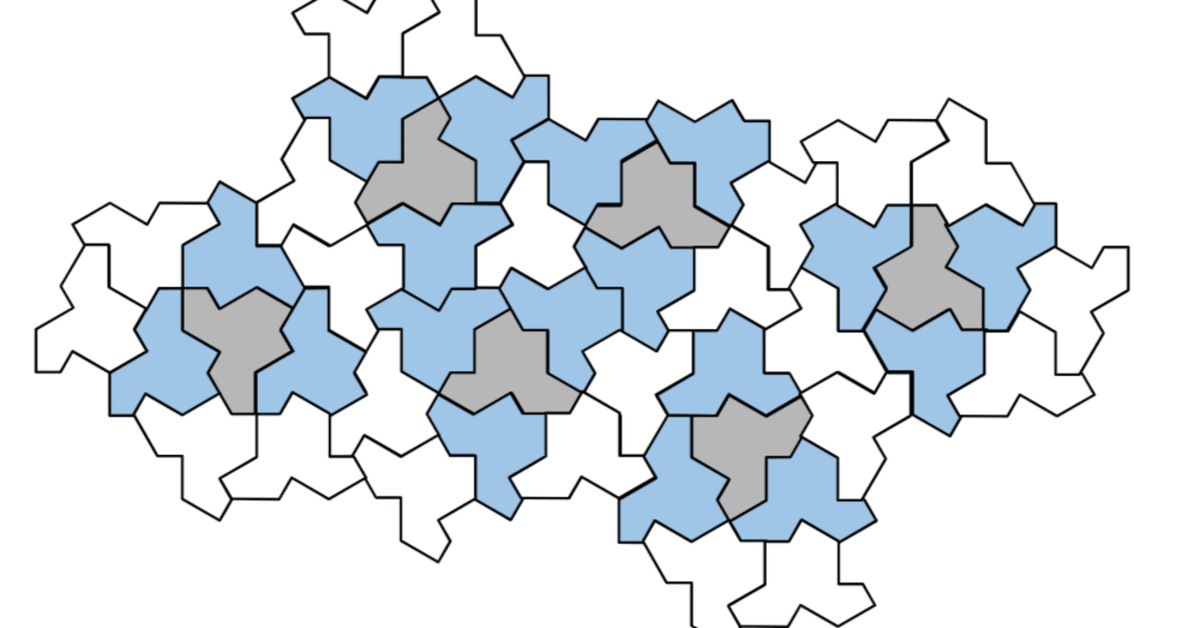
論文「An aperiodic monotile」から、18ページにある、図2.11。

Figure 2.11
https://doi.org/10.48550/arXiv.2303.10798
左から2番めの図形を拡大して、少し角度を変えたのが、以下の図です。

HATの個数は(H7を1組、H8を5組からなるので)47です。
ボードゲームの盤面としては非対称ですが、マスの数が50個近いのは手頃なサイズです。
3種類に塗り分けていますが、灰色のHATは他の2色HATの裏返しになっています。
さらに、それぞれのHATは辺で隣接しているHATの個数は、以下のようになります。

HAT HALMA
この盤面を使ったボードゲームを考えると、パッと思いつくのが『Halma(ハルマ)』とか『ダイヤモンドゲーム』です。
ハルマは、コマを飛び越しながら進んで、すべてのコマをゴールに到達させるアブストラクトゲームです。

赤と緑のコマは各10個。
それぞれの陣地(赤・緑)からスタートして、互いコマを動かし、相手の陣地(緑・赤)にすべてのコマを到達したほうが勝ちです。
ちょっとしたオプションとして、裏返しHATのマスには、中立コマを置きます。
中立コマは動かすことはできません。
コマの動かし方ですが、辺に隣接するマスに移動します。
ただし、移動したマスに駒がある場合はジャンプして、さらに辺に隣接する空きマスに移動します。
さらに、移動したマスに駒がある場合はジャンプできます。
ただし、1回の移動で一度ジャンプしたり移動したマスに2回以上行くことは禁止とします。

赤の最後のジャンプは、中立コマを2回通過する
ことになるので禁止です。
盤面が非対称なので、赤と緑のどちらが有利なのでしょうか(どなたかわかる方、教えてください)。
隣接した辺を塗り分けてみる
HATの盤面のマスは、辺で隣接するマスの数は4〜6です。
5個隣接するマスは一旦無視して、気になるのは4個隣接するマスと6個隣接するマスは、対辺を1組にして塗り分けできるかです。

右:白色HATは6辺隣接しているので、赤・青・緑で対辺のセット
試しに挑戦してみると、以下の図のように塗り分けることができました。

塗り分けてみると、
・白色マスは、時計回りに赤・青・緑の順になっている
・3辺が接している端点では、3色が1本ずつある。
・4辺が接している端点では、2本ある同色の辺は一直線につながっている

といった特徴があります。
更に盤面を拡大すると、破綻なく塗り分けられるのか、ちょっと心配。
この性質を使って、新たなゲームのルールを考案できるかもしれません。
締め
ということで、アインシュタインタイルを使った盤面を考えてみました。
正方形や正六角形の一般的なマスとは異なる可能性がありそうです。
結構いじりがいがありそうです。
では。
