□□□とボードゲーム（１．６１８）〜デュシャンとチェス（続々々々々：超マス）

前回の記事はこちら。

前々回の宿題をしないまま終わりました。
さらに、ちょいとした体調気分不良の「のほほ〜ん」状態となってけっこう休んでしまいました。
ごめんなさい。

さすがに今回は宿題を片付けます。
なお、ナンバリングは黄金比（1.618…）の近似になっていますが、たまたま気づいて悪乗りしているだけで、記事の内容とはほぼ無関係です。

前々回の宿題と個人的妄想

で、前々回の記事はこちら。

残していた宿題はこちら。

ポスターでは、立方体は２１個描かれています。
多数の立方体を描くために、ブロックを袋に入れて撮影した写真をモデルとしました。
とすると、他のブロックの裏に隠れているものが何個かあってもおかしくないよね？（※「Tout-Fait」の記事には、その話題は書かれていませんでした）

果たして、デュシャンは袋にブロックを何個入れたのでしょうかね。

正解はわかりません。
わかりませんが、四次元に興味をもったデュシャンならば、と妄想しつつ仮説を立ててみます。

袋に入れたブロックの個数は２４個。
描かれなかったブロックの個数は３個。

です。

正八胞体（四次元超立方体）

デュシャンの1925年のポスターに描かれた立方体のブロックは、三次元化したチェス盤のマスを表しています。

で、この立方体マスを同じようにもう一次元あげてみます。
これは、四次元化した超立方体（正八胞体）のマスです。

正八胞体 - Wikipedia

超立方体について - 緑茶思考ブログ

引用：https://yusuke-ujitoko.hatenablog.com/entry/2017/04/01/022305

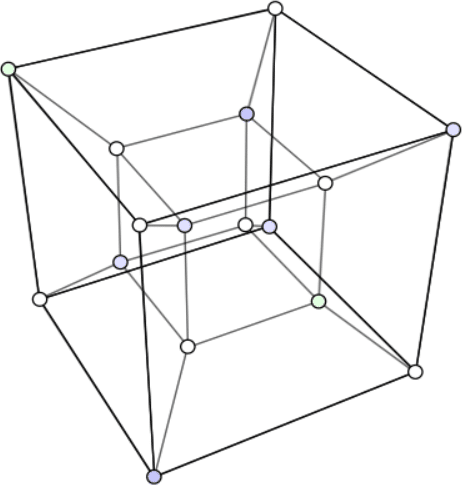
正八胞体というのは、三次元の立方体が６個の正方形を組み合わせた図形であるように、四次元超立方体は８個の立方体を組み合わせた図形になります。
上の図を見ると、中央に小さい１つの胞体があり、その周り４箇所と上下それぞれ１箇所に合計６つの胞体があり、図形の外側に大きな１つの胞体で、あわせて８つです。

正八胞体は下の図のように表すこともできます。

小丸は正八胞体の頂点

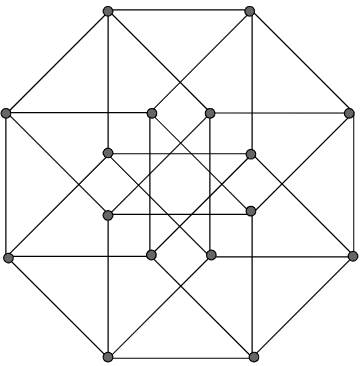
さて、正八胞体を構成する正方形の数をみてみます。
１つの胞体は立方体ですので、６個の正方形から成り立ちます。
胞体は８個あるので、単純に数え上げると４８個です。
しかし、どの正方形も２つの胞体（立方体）の面が接しているので、その半分の２４個となります。

正方形を赤線および青線で囲ってみる

さらなる特徴として、立方体だと辺で接しない２つの面が３組あるように、正八胞体は、面で接しない２つの胞体が４組あります。

立方体と、その２つの面が接しない３組

正八胞体の２つの胞体が接しない４組

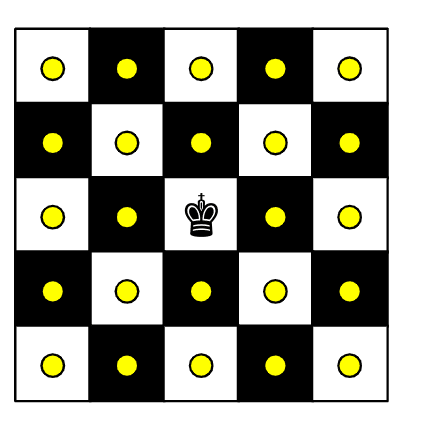
おまけですが、キングと２４マスの組み合わせの特徴を。

通常のチェスで、キングが２回移動することで到達できるマスは２４個あります。

キングは、タテ・ヨコ・ナナメに１マス移動できます。

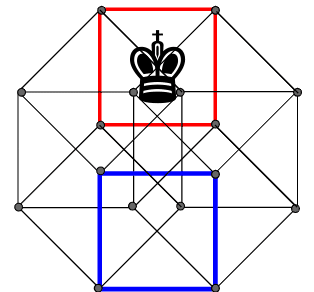
さて、正方形のマスからなる正八胞体の盤面を考えてみます。
１つの胞体つまり立方体の面の１つがマスになります。
マスは２つの胞体に含まれていますので、キングはそれぞれの胞体での辺に接するマスに移動できます。

それぞれの胞体でのキングの移動できるマス（赤線で囲う：各４）。
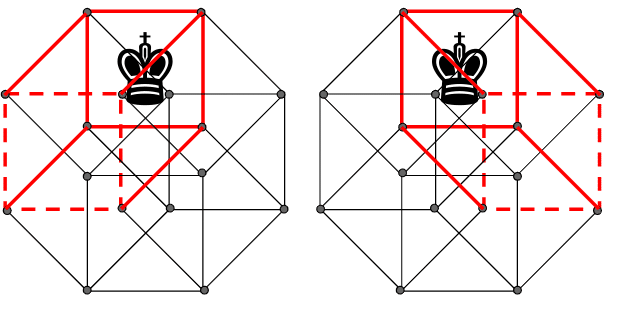
点線で囲ったマスは、１回移動では到達できない。

胞体の向かい合う面には移動できない（２回移動が必要）ので、合計すると８マスに移動できます。
通常のチェスと同じく８マスなのが面白いです。
では正八胞体の盤面でキングを２回移動するとどうか。
１マスだけ３回移動でないと到達できません。

青く囲ったマスは、キングの２回移動では到達できない。

描かれないブロック

２４個の妄想はこの程度にして、次は描かれないブロックがなぜ３個か、です。

ある意味シンプルです。

チェスの勝敗が着くのに必要な
コマの最低数は３個

です。
まず、何よりもそれぞれのプレイヤーのキングは欠かせないので２個いります。
その一方、キングだけでは勝敗がつきません（チェスでは、相手に捕獲されるようにキングを移動することができないので、結果引き分けになってしまう）。
キングを詰め（チェックメイト）するコマがどうしても１個必要になるので、合計３個です。

コマが置かれているマスは、当然空きマスではありません。
つまり、ポスターに描かれたブロックはすべて空きマスのブロックだ、と妄想してみました。

２４マスの盤面の作品

ところで、デュシャンの作品にはチェスのモチーフが含まれているものが少なくないわけですが、ネルソン・アトキンス美術館が収蔵している作品に「Marcel Duchamp Cast Alive（マルセル・デュシャンの生きた鋳像）」があります。

Marcel Duchamp was born July 28, 1887 #onthisday. His self portrait “Marcel Duchamp Cast Alive" reveals the artist's love of chess. He earned the title of chess master and published a treatise on the game in 1932. On view in #BlochGalleriesKC P29. pic.twitter.com/kbPC4cSnxW

— Nelson-Atkins Museum of Art (@nelson_atkins) July 28, 2019

引用：https://twitter.com/nelson_atkins/status/1155515004814315520/photo/1

左上の顔の鋳像は、デュシャン本人のライフマスク（存命中の本人の顔）です。
デュシャンがチェス盤を見下ろしていますが、このチェス盤――２４マスなんです。
まあ、偶然、でしょうけどねえ。

締め

ということで、引き延ばした宿題をようやっと出すことができました。
色々と失礼しました。

デュシャンとチェスは掘り出すとドサドサ発見があって面白い。
とはいえあと１回やって一休みして別の話題に浮気しようかしら、なんて考えてもいます。
どうしましょ。

次回もよろしくです。

では。