
【21世紀版フランス革命の省察7パス目】背景にある筈の「統治の数理」についての推察
以前の投稿でしたこの話…
当時の欧州における社会変遷は激しく、わずか数年でも激変していきます。ましてやマルクスはドイツ人でフランス史の門外漢。せめて「我々ドイツ人の絶対王政からの脱却欲とフランス人の秩序回復欲は半径を同じくする同一円弧上の対蹠かもしれない」と想像出来ていたなら…
考えてみれば「やがて来るべき国王と教会の権威からも資本主義的誘惑からも解放された新人類プロレタリアート」問題を解決するのは科学実証主義的アプローチ、すなわちその数理的解釈による全体像俯瞰かもしれません。
「リーマン尺」概念の導入
話を簡便化する為に、ここで「リーマン尺」概念を導入します。
乗法単位元「1」を中心として$${α^{x}}$$と$${α^{-x}}$$の値が0から1になる範囲を貼り合わせ、-♾️から+♾️の範囲を0から2の範囲で表そうというアイディアですね。

これはロジスティック方程式における適正値「1」に収束する範囲とも対応しています。

「統治適性ライン」概念からの出発
あちらの筋の方々は好んで「権力勾配」なる意味不明の造語を用いますが…
実在するのは「権威勾配」の概念。
例えば軍隊における将校と兵卒、医療現場における医師と看護婦/看護夫における指揮系統と、バンドメンバーそれぞれが果たす役割ではベクトルの定向性に関する要求が全く異なる訳で、それを数値尺度化したものと考えて下さい。これを水平評価尺度に取り、垂直評価尺度に「統制満足感」を取ると、ある種の対角線=傾きとして「統治適性ライン」が浮かび上がってきて、各状況を「権威勾配の過剰」と「権威勾配の過小」の二状態に分類出来る様になるのです。

まさしくAI理論の初歩「分類と回帰」概念の導入という次第。
総務省統計局「機械学習(教師あり学習)」
「統治満足度」とは分断状態にあった近代以前のイタリアにおいて、統治者自体はコロコロと変わっていくものの領土としては比較的長期間に渡って同一性を維持したナポリ=シチリア両王国において、特に支配者がスペインからオーストリアに推移して思想的自由度が増した時期に形成されたナポリ経済学を出発点とするイタリア経済学における重要概念。
水平評価軸に「統治負荷=(徴税や兵役といった)領民側の負担」、垂直評価軸に「統治効能=(治安維持や出国時の各種手形発行といった)領民側が対価として受ける公的サービス」を置き、さらに「任意の統治負荷に釣り合う任意の統治効能が存在する」と考えた時に浮かび上がってくるある種の対角線=傾きが「統治満足度」となります。

もちろん実際にはどちらの評価軸も非線形で、簡単に答えは導出する事が出来ませんが様々な考え方の出発点に使えて中々便利。もっともカール・マルクスは「資本論(Das Kapital. Kritik der politischen Ökonomie, 1867年~1894年)」の中でこの考え方を全面否定しています。
経済学はドイツでは今日までは外国の学問であった。グスタフ・フォン・ギューリヒは、『現代主要商業諸国における商工農業の歴史的叙述』において、とくに1830年に公刊された彼の著作の最初の二巻で、わが国における資本主義的生産様式の発展を、したがってまた近代ブルジョア社会の建設をもはばんでいた歴史的事情を、すでに大いに論じている。すなわち、経済学の生きた地盤がなかったわけである。経済学は、完成品としてイギリスとフランスから輸入された。ドイツの経済学の教授たちはいつまでも生徒であった。他国の現実の理論的表現であるものが、彼らの手中にあっては一つの学説集に転化され、自分たちを取りまいている小市民世界の意味に解された、すなわち曲解された。きれいに払いのけるわけにはいかぬ学問上の無力感と、実際に他国のものである領域で教師口調で説明しなければならぬというおちつかぬ良心とを、文献史的博学で美装したり、いわゆる官房学といういろいろな知識の混合物から借りたよその材料を混ぜこんだりすることによって覆ようにした。この官房学の浄化火こそがドイツ官僚制の希望にあふれる候補者が、耐え抜かねばならないものなのであった。
そう、ここに登場する官房学(Kameralismus)もまたナポリ経済学の支流。ただし絶対王政護持の立場から(国庫を膨らませる最優先と考える)フランス重金主義(Bullionism)などの要素も混ぜ合わされてかなり別物へと変貌してましたからマルクスに全面否定されるのも仕方なかったかもしれません。
さて、この様に水平(評価)軸に「権威勾配」、垂直(評価)軸に「統治満足度」を置くとどんな景色が広がる事になりましょうか。

この様に、まず真っ先に浮かび上がってくるのが「三種の極限において、両者の相関関係が崩壊する」なる数理。姿勢制御問題における「ジンバルロック」概念ですね。
①権威勾配が無限大(+♾️)で、統治満足度が無限小(-♾️)の場合…斜に構えてこの状況を「権威勾配が存在する限り、統治満足度は0のまま」と捉えたのが、カール・マルクスの絶対王政ドイツ論となります。
国王は,政治を独占することで,臣民を実利的な世界に封印する。しかしそれが君主政の本質なら,永遠に臣民は自由を獲得し,政治を行うことなどできない。だから,臣民が自由を獲得すれば,プロイセン体制は崩壊するしかない。理論的には,改革などありえないのである。
②権威勾配が無限小(+♾️)で、統治満足度も無限小(-♾️)の場合…斜に構えてこの状況を「権威勾配が存在しない限り、統治満足度は0のまま」と捉えたのが、皇帝ナポレオン三世を選んだフランス国民の心理となります。
人びとは田舎を讃美し、無学な人間のほうが、そうでない人たちよりも生まれながらにしてより良識を身につけているとされた。憎しみが世にはびこっていた。小学校教師に、酒屋にたいする憎しみ。哲学の授業に、歴史の講義に、小説に、赤いチョッキに、長いひげにたいする憎しみ。そして、独立不羈をとなえるあらゆるものに、すべての個性の表明にたいする憎しみである。権威主義を立てなおす必要があったからだ。それがいかなる名のもとに行使されようと、どこから到来するものであろうとかまわない、力であり、権威でありさえすればよかった。
③権威勾配が0の場合。これを権威勾配と統治満足度の相関関係の在り方の一部と捉えるか、斜に構えて「権力勾配と統治満足度の関係は無相関」と考え次元削減するかによって理論の組み立てが変わります。科学実証主義の世界観は後者寄り。こういう状況を「全微分が通った」と捉え「とりあえず無視可能」と条件を付けて次元削減します。さらに踏み込んで「例え0になる条件を捉えられなくても、所定の条件下で定数と扱えれば計算を進められる」と考えるのが微分方程式における偏微分概念となる訳です。
そもそもリーマン球面もロジスティック方程式もその極限がεδ論法によって定められている為、上掲の①の場合にも②の場合にも到達しません。逆に観測原点(加法単位元0や情報単位元1)からは+♾️とも-♾️とも観測される無限遠点$${\tilde{x}}$$にいくら数量を加減しても、それが加算範囲に到達する事はないのです。
この辺りが、彼の考えた「国王や教会の権限とも資本主義的誘惑とも全く無相関な新人類プロレタリアート」がいつまで待っても現れない理由といえそうです。
領主と領民の立場が交錯する近代社会
そもそもここでは「領主(国主)と領民(国民)」の関係を定数的に扱いましたが、上掲の「軍隊や医療現場の指揮系統とバンドマンの役割分担における権威勾配概念の差異」を考慮に入れると、さらにもう一つ「立場勾配」なる評価軸が追加される訳ですね。
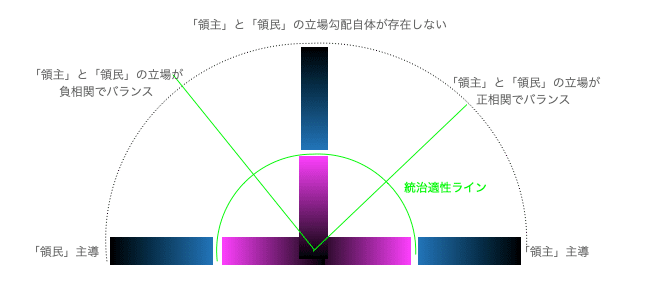
ここでさらに「権威勾配」と「立場勾配」のそれぞれに「領主寄り発想から領民寄り発想への推移」ベクトルと「領民寄り発想から領主より発想への推移」ベクトルを視野に加えると、最終的に完成する数学的構造は「統治適性値」を半径、「権威勾配」と「立場勾配」をそれぞれ小半径と大半径の角度に割り振ったある種のトーラス構造となります。




結果として「統治満足度」概念がとりあえず表面的には視野外に追い出されてしまう(その一方で、背景としてその要素が大きく関与してくる事が示唆されている)あたりが興味深いところですね。まさしく合成関数を連鎖率(チェーンルール)を用いて解く考え方そのもの。すなわちここでもし「立場勾配」もまた「権威勾配」同様、統治負担と統治効能の対角線で表せる想定したなら、統治負担u、統治効能v、立場勾配x(u,v)、権威勾配y(u,v)と置いて以下の式が成立する事になります。
$${\frac{\partial f}{\partial u}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial u}}$$
$${\frac{\partial f}{\partial v}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial v}}$$
天動説の時代の人間がなかなか地動説概念に到達出来なかった様に、カール・マルクスもまたこういう考え方に容易には到達出来ず「(決して現れない)あらゆる権威勾配概念と統治満足度概念と無相関な新人類プロレタリアート概念」が非現実的と悟って以降も、生涯その概念の完全棄却には至らなかった様です。とはいえそれが現れるのは遠い未来の事とし、自分の理論からは切り捨てたのは英断といえましょう。
「グラムシの市民社会論」の登場
こうした数理、実は「ユーロ・コミュニズムの父」グラムシの市民社会論にも沿った展開だったりします。
フランス絶対王政や帝制ロシアや中華王朝で暴力革命が成功したのは、時代遅れになりつつあった因循姑息な旧体制が、成長を始めた市民社会形成の阻害要因になっていたからである。
イタリア王国においては既に体制が市民社会形成の妨げとなっていなかったのに、それどころか新興国家発展の為に国民が一丸とならねばならい大事な時期だったのに、共産主義者はあくまで暴力革命を志向してイタリアの政情不安を煽る様な真似ばかりしてきた。それで国民を敵に回してしまい、そういう共産主義者を「国民の共通敵」認定する形で人気を高めた「共産主義の紛い物」ファシスト党にみすみす政権を取らせてしまったのである。
後進国と異なり、早くもイタリアルネサンス期から市民社会の形成が始まっていたイタリアにおいては、共産主義者は別の戦い方をすべきだった。
「共産主義の紛い物」…まぁ元々は熱心な共産党員だったムッソリーニが「マルクスの思想からええとこどりした」ファシズム理論を掲げて政権を奪取し、その結果投獄されて獄中で練ったアイディアなのでこういう考え方になったとも。
それにつけても「ええとこどり」とは? 実はここでもマルクスが執着しつつも理論外に追いやった筈の「国王や教会の権限とも資本主義的誘惑とも全く無相関な新人類プロレタリアート」理論が思わぬ形で援用をされた形跡があるのですが…その話を始めると長くなるので、また機会を改めて。
ここで「ムッソリーニの師匠」の一人として、上掲のイタリア経済学派の重鎮パレートの名前が挙がる辺りに話のややこしさが潜んでいるのですね。
そう、常に付きまとってくるのが「効用とは何か?」という問題…
日本国語大辞典:
個々の人間が財貨や用役に対して感ずる主観的な欲望充足の度合い。
デジタル大辞泉:
経済学で、消費者が財やサービスを消費することによって得る主観的な満足の度合い。
改訂新版世界大百科事典:
個人や家計は,みずからの欲望や好みにもとづいて,経済活動の最終的な成果である財やサービスを選択し消費する。この消費する主体にとっての,欲望充足の度合の主観的測度を効用と呼ぶ。いいかえれば,欲望・嗜好を充足させる財・サービスの消費者にとっての使用価値,ないしは有用性ということになる。効用は,消費対象に内在する固有の性質だけでなく,消費主体によるその対象物の評価によって大きさが決まるため,しばしば主観的価値とも呼ばれる。一定量の砂糖がどれほどの効用をもつかを一意的に表現することはできないし,ミルクからの効用をそのままそれに足し合わせることもできない。また,ある個人が受けたある財の効用を,別の個人のそれと比較することはできない。効用には(重さや長さのような)測定単位がないからである。このような効用の可測性の問題は,F.Y.エッジワースの無差別曲線の理論や,パレートの選択理論(パレート最適)の展開によって克服された。
効用が価値理論の発展にとって重要なきっかけを与えたのは,限界効用という概念である。それは,〈価値のパラドックス〉と呼ばれる問題に理論的解答を与えるものであった。アダム・スミスによる考察はよく知られているが,このパラドックスは次のようなものである。財の有用性ないしは効用は,必ずしも価格を反映しない。たとえば水は,きわめて有用であるが,豊富であるがゆえに安価である。他方,水と比較して有用性の少ないダイヤモンドが,希少であるという理由で高価なのはなぜか。このパラドックスは,限界効用,すなわちある財の限界的1単位の効用という考え方を用いることによって,次のように説明される。限界効用は,消費者が価格を支払って購入しようとする財の最終単位の主観的有用性のことであり,その大きさは彼の保有する財の全量に依存し,その保有量が増加するにつれて一般に逓減するという性質をもつ(限界効用逓減の法則)。水の全効用は確かに大きいが,水は一般に望むだけ保有しうるから,水の限界1単位の効用(すなわち水の限界効用)はきわめて小さい。したがって水は廉価である。他方,ダイヤモンドの全効用は水に比べて小さいとしても,一個人が保有しうる量は少ないためその限界効用は大きく,したがって高価であると説明できる。次に,限界効用逓減の法則が成立すると仮定すれば,限界効用と価格の比がすべての財について等しくなるように消費財の組合せを購入すれば,消費者の効用は最大となる。これは〈限界効用均等の法則〉と呼ばれ,発見者ゴッセンの名にちなんで〈ゴッセンの法則〉とも命名されている。これは,消費者が一定量の貨幣を種々の消費財購入にあてるとき,最も満足の大きい(効用を最大化する)支出方法を保証するための必要条件を与える。なぜなら,もし限界効用を価格で割ったものが,ある財と他財とで等しくなければ(すなわち1円あたりの限界効用が等しくなければ),その比の低いほうから高いほうへ支出を移転することによって総効用を増加させることができるからである。この推論にとって重要な仮定は,〈限界効用逓減の法則〉が成立しているということである。
このような効用理論は,その後大いなる精緻(せいち)化を受けると同時に,個人を超えて社会全体にも拡張して適用されるようになる。エッジワースやパレートの考えた無差別曲線(面)の概念は,等しい効用を与える財の集合を示す等効用曲面(地図の等高線のようなもの)であるが,ここで問題となるのは,ある等効用曲線が他のそれと比較して高いか低いかだけであり,その差がどれほどであるかは問題とはならない。すなわち,効用の基数的大小関係ではなく,序数性(順序関係)のみが問題となる。ここにおいて効用は測度の単位選択および測定の問題から解放されたのである。また,本来個人の主観的評価である効用概念を,社会全体に適用した(社会内部の全個人の効用の集合として)社会的効用あるいは社会的厚生関数という概念が厚生経済学などで使われている。
ついでにChatGPTに尋ねてみた結果。上記解説では福祉分野に限定して言及されている「効用関数」概念が一般化されてるあたりに「特徴の抽出を生業とする」AIらしさを感じずにいられません。というより、今やそれが世界常識で、ChatGPTはそれを学習しただけとも?
経済学における「効用(utility)」は、個人が商品やサービスを消費する際に得る満足や利益の度合いを指します。効用は主観的であり、異なる個人や状況によって異なる程度で感じられます。経済学者は、効用を通じて個人の選好や意思決定を理解し、分析します。
以下に、効用に関連するいくつかの重要な概念を説明します。
限界効用(Marginal Utility):
ある商品やサービスの消費量を1単位増やしたときの、追加の効用のことを指します。限界効用は、個人が最後の1単位をどれだけ価値あると感じるかを示す重要な概念です。
効用関数(Utility Function):
ある組み合わせの商品やサービスに対する総効用を表す関数です。通常、効用関数は個人の選好や好みを数学的に表現したものであり、異なる組み合わせの効用を比較するために使用されます。
効用最大化(Utility Maximization):
制約の中で個人が効用を最大化しようとする行動の原則です。個人は限られた予算や資源を使って、最も自分にとって価値のある商品やサービスを選ぶことを目指します。
効用の逓減法則(Law of Diminishing Marginal Utility):
特定の商品やサービスを増やしていくと、その追加の単位に対する効用は徐々に減少していく法則です。これは、最初に消費したときほど同じ商品やサービスの効用が高くないという考え方を表しています。
経済学では、個人の効用を分析することで、市場や経済全体の動向や意思決定の理解を深めます。
そう、効用概念tは上掲の統治負担uと統治効能vを合わせた概念と考え、立場勾配x(t)、権威勾配y(t)と置けば上掲の式が以下の様に単純化されるのです。
$${\frac{\partial f}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}}$$
例えばここでいう「効用」概念を市場経済外まで適用するとどうなるでしょう? 経済人類学者カール・ポランニーは「市場経済は独立する以前は社会に埋め込まれていた」と指摘。太陽を動かし続ける為に人身供犠を続けたアステカ文明と生贄の調達手段としての花戦争、独特の非市場経済を発達させたダホメ王国、インディアンやエスキモーのポトラッチなどが実例として挙げられてきた歴史があったりもするのですね。
そう、偏微分概念はこういう形でのポリモーフィズム性も内包していたりするのです。
また、ここでいう「領主的立場と領民的立場の中点」や「権威主義と反権威主義の中点」は「統治適正値」と無相関になった、すなわち誰もがそれから解放された平等状態とも限らない点に注意が必要です。先に上げた例で説明すると「軍隊における将校と兵卒の関係」「医療現場における医師と看護婦/看護夫の関係」が一方的なのは、身分秩序と無関係に仕事内容の厳粛な要請に従っての事。一方「バンドにおける各メンバーの役割」はそれぞれの個性と技能ばかりか、曲ごと、いやそれどころか展開ごとに異なってくるばかりか「作詞作曲を外部委託する」「ゲストメンバーを呼ぶ」「(マネタイズを意識して)聴衆の期待に応える」といった複雑な要因が絡み合い、ただ「領域として閉じている」のでそのベクトルとしての総計が0になってるだけなのです。すなわち統治適正値は消失するどころかむしろ必要な次元数に分解され、より精緻に運用されていると考えるべきなのですね。


こうした2変量解析概念の発展形として多変量解析概念が現れ、その技法の一つたるロジスティック回帰分析辺りから機械学習概念が分岐し、21世紀に入ると遂にパラメーター(確率計算を行うための係数の集合体)数が$${2^{10000}=10^{30}}$$を超える大規模言語モデル(LLM=Large Language Model)まで現れてしまったという展開なのですね。
なお、この段階で擬似相関が疑われる場合には偏相関係数を計算。
ロジスティック回帰分析
$$
{P=\frac{1}{1+e^{-(β_0+β_1x_1+β_1x_1+…+β_nx_n)}}}
$$
操作変数$${x_1,x_2,…,x_n}$$の入力に対し、目的変数Pを確率(0≦P≦0)の形で出力して返す。
切片$${β_0}$$や、偏回帰係数$${β_1,β_2,…,β_n}$$といったパラメーターは、あらかじめ与えられたデートセットからニュートン=ラプソン法(最小二乗法)や最尤法などによって求めておく。

ロジスティック回帰は、機械学習の一種で、主に分類問題に使用されるアルゴリズムです。機械学習は、データからパターンを学習し、その学習結果を元に未知のデータに対して予測や判断を行うための手法やアルゴリズムの総称です。以下に、ロジスティック回帰と機械学習の連続性について詳しく説明します。
ロジスティック回帰の概要:
ロジスティック回帰は、回帰という名前がついていますが、実際には分類問題に使用されます。具体的には、2クラス分類(2つのクラスにデータを分類する)が一般的です。
ロジスティック回帰は、線形回帰の一般化であり、線形な関数を用いて確率を推定します。確率の推定は、シグモイド関数(ロジスティック関数)を用いて行われます。シグモイド関数によって、出力は0から1の範囲に収束します。
機械学習とロジスティック回帰:
機械学習は、データからパターンや規則を学習するための手法です。ロジスティック回帰は、その中の一つで、特に教師あり学習の一部です。教師あり学習では、アルゴリズムに学習用のデータ(入力と対応する出力)を提供して、アルゴリズムがそのパターンを学習します。
ロジスティック回帰モデルも、機械学習の一環として学習されます。訓練データを用いてモデルを学習させ、未知のデータに対する予測を行います。
連続性:
ロジスティック回帰は、機械学習の一部であるため、機械学習の範疇に含まれます。
機械学習には他にも多くの手法やアルゴリズムが存在し、それらは異なる問題に対応するために使用されます。例えば、決定木、サポートベクトルマシン、ニューラルネットワークなどがあります。
簡潔に言えば、ロジスティック回帰は機械学習の一種であり、特に分類問題に利用される手法の一つです。機械学習全体では、さまざまな手法があり、それぞれ異なるデータや問題に適しています。

こうした数理概念の進化は社会にどういう影響をもたらしてきたのでしょうか。例えば第一次世界大戦以前の歩兵が「中隊(300人前後)」単位で移動し、一斉射撃し、一斉突撃するのが精一杯だったのに対し、それ以降は火力減少を軽機関銃などの導入によって補いつつ、分隊(10人前後)単位で複雑な機動戦を展開する様になりました。まずは個人が判断しなければならない内容の爆発的増大とそれに伴う緊張感の高まりに耐え得る近代人が教育によって生み出され、産業革命導入や選挙権拡大をも支えてきたのです。そして、こういう話が「シィエスのフランス革命」において「フランスでは、そうした近代的教育革命に最初に取り組んだのがコンドルセ侯爵とシィエスだった」とされた話へとつながっていくのです。
こんな感じに全体像がまとまったあたりで以下続報…
