
【数学的溢れ話14パス目】60進法こそ「e進数(ネイピア進数)」概念の大源流?
まだまだメモ段階もいいところですが、最近「e進数(ネイピア進数)なるもの」についてしばしば考え込む様になりました。
人類の数学が本格的に「カンブリア爆発期(5億4200万年前~5億3000万年前)に授かった視覚と視覚情報を処理する脊髄」の制約から脱し始めたのは、ある意味自然指数$${e^x}$$と自然対数$${log_ex}$$の概念に到達して以降といわれています。すなわちネイピア数e=2.718282…の発見がパラダイムシフトを引き起こしたともいえましょう。
$$
ネイピア数e=\lim_{n→\tilde{∞}}(1+\frac{1}{n})^n=2.718282…
$$
会計期間ごとに1増える単利計算(…,前期0,当期1,来期2,…と加法的に増大)は、以下の様に複利計算$${(1+\frac{1}{n})^n}$$でn=1の場合に対応する。
$$
前期(1-\frac{1}{1})^1=1-1=0
$$
$$
当期(1±\frac{0}{1})^1=(1±0)^1=1^1=1
$$
$$
来期(1+\frac{1}{1})^1=1+1=2
$$
nの次数を無限に引き上げ続けると、それぞれ以下の無理数に収束する。
$$
前期\lim_{n→\tilde{∞}}(1-\frac{1}{n})^n=e^{-1}=0.3678794…
$$
$$
当期\lim_{n→\tilde{∞}}(1±\frac{0}{n})^n=(1±0)^n=1^n=1
$$
$$
来期\lim_{n→\tilde{∞}}(1+\frac{1}{n})^n=e^{+1}=2.718282…
$$

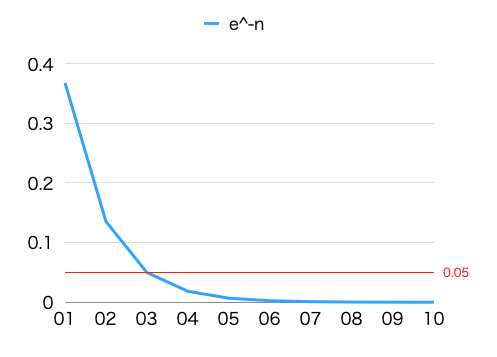
坂の勾配でいうと45度の急勾配ですから一つのグラフにまとめて表示するのも一苦労。この辺り「カンブリア爆発期(5億4200万年前~5億3000万年前)に授かった視覚と視覚情報を処理する脊髄の末裔」で情報処理する我々はどう対処してきたのか? なんと天然の世界に偉大なるマスターピースが存在していました。そう「地平線」や「水平線」の概念がそれだったのです。

$$
e^{θi}=\cos(θ)+\sin(θ)i(-π≦θ≦+π)
$$
「左から右」「右から左」「どちらにも見える」



「上から下」「下から上」「どちらにも見える」



「内から外」「外から内」「どちらにも見える」



実は、こうした考え方に重要なインスピレーションを与えてくれたのが劇場版アニメーション「ジョゼと虎と魚達(2020年)」だったのです。絵を描いて身を立てたいと考えている(アニオリ設定)車椅子少女ジョゼちゃんさんは、せっかく画才を備えていながら家からほとんど出た事がなく、全部独学なので遠近法も身についてない一方、海の水平線と海底の無重力感に憧れます。そんな彼女ならおそらく「その全体像を可視範囲に収めるのが大変な」自然指数のグラフを目にしても「なんか全然ピンときいへん」としか言わないだろうなぁと…まぁその辺りが発想の出発点だった訳ですね。
独学なので遠近法も身についてない…ラスト近くの紙芝居絵では「上空から神々しく降り立つBパーツ」でちゃんと表現されており、彼女の成長を窺わせる。まぁこの「Bパーツ」、最後いらない子扱いされて、溶けてなくなっちゃう可哀想な存在な訳なのだが…
おそらく「カンブリア爆発期(5億4200万年前~5億3000万年前)に授かった視覚と視覚情報を処理する脊髄の末裔」を用いて視覚情報を処理する処理する我々は、最初から「自然指数関数$${e^x}$$」概念を「虚数概念$$i^2=-1$$」と一緒くたに扱ってきたのであって、その結果は「地平線・水平線イメージを引き摺った」透視図法や片対数グラフの構成方法にしっかり痕跡を残しているという次第。
$$
-1=i^2=e^{2*\log_e(i)}=e^{2*\frac{1}{2}πi=e^{πi}}
$$
$$
ただしi^2のe^{2log(i)}への変換に底の変換公式a^b=e^{log(a)b}を使用した。
$$

同様に近世まで数学や物理学の世界が「時間の流れの非可換性に無頓着」だったのも上掲の「(中割りがないアニメーションが)どっちにも見える認識バグ」と密接な関係がある様なんです?
すでにバビロン人の時代に遡って蝕が予知出来る一定の時期で起こり、その周期は過去に向かっても将来に向かっても一定である事が認められていた。時間そのものも、恒星の運行から測定するのがほかの方法で測定するよりもよいことが知られていた。太陽系に生じるすべての現象の様式は、プトレオマイオスの周転円の形式であっても、あるいはコペルニクスの軌道説の形式であっても、車輪または一連の車輪の回転によってあらわされる。ここでは未来は一定の様式に従って過去を繰り返すものである。天球の音楽は前から聞いても後から聞いても同じであり、天文学上の事柄は過去に向かっても将来に向かっても同じように起こる。天体の相互位置を示す為の天球儀を右に廻しても左に廻しても、初めの位置と方角を除いては何の違いも生じない。最後にこれらすべてのことがニュートンによって一連の公理系としてまとめられたとき、この力学の基本法則は時間変数tを変換しても不変のものとしてあらわされた。
(しかし実際には)重力の天文学さえ運動を減衰させる摩擦過程を含んでおり、厳密にニュートンの図式に合うような科学は一つもない。生物学は完全に一方向向きの現象を扱っている。誕生は死の正反対のものではなく、組織の発達を意味する同化作用は、組織の破壊を意味する異化作用の正反対のものではない。細胞の分裂も時間的に対象な様式では行われないし、受精卵をつくる生殖細胞の結合も同様である。個体は時間的に一方向を向いた矢であり、種族も同様に過去から未来に向けられている。古生物学の記録には、断絶したり錯綜したりはしているが、単純なものから複雑なものへと進む長期にわたる決定的な傾向が見られる。
古代バビロニアまで遡る叡智「60進法」
ところで以前、地球平面論者の視界が「地球の球面性をギリギリ意識しないで済む範囲=地球を縦横に60分割した(1辺約670km前後の)微小領域」に限定されている可能性があるという話をしました。

「60分割」というとネイピア数の近似としてもそう悪くない精度。
$$
(1+\frac{1}{60})^{60}=2.69597(\lim_{n→∞}(1+\frac{1}{n})^n=2.718282)
$$
$$
(1-\frac{1}{60})^{60}=0.3647923(\lim_{n→∞}(1-\frac{1}{n})^n=0.3678794)
$$
これを用いて「1分=60秒」「60分=1時間」「1周360度」といった60進法(Sexagesima)の枠組みを構築したバビロニア天文学こそ、ある意味e進数(ネイピア進数)の真の開祖というべきかもしれません。
60進法(セクスゲシマル)は、数の記数法の一つで、基数が60である数体系です。この体系の成立は古代メソポタミア文明に遡ります。
起源と成立
古代バビロニア: 60進法の起源は、紀元前2000年頃の古代バビロニア(シュメール・アッカド文明)にあります。バビロニアの数学者たちは、60を基数とする数体系を発展させました。60という数は、1から6までの全ての数(1, 2, 3, 4, 5, 6)で割り切れるため、分数計算や角度測定などで非常に便利でした。
実用性: この体系は、天文学や測量、時間の計測において非常に実用的でした。例えば、1時間を60分、1分を60秒とする時間の単位や、360度を基本とする角度の測定法は、60進法に基づいています。
伝播と影響: 60進法は、バビロニアから他の古代文明にも影響を与え、特に天文学や暦法の分野で広く採用されました。この影響は、現代においても時間や角度の測定方法に残っています。
まとめ
60進法は、古代バビロニア文明で実用的な理由から発展し、天文学や測量において重要な役割を果たしました。その影響は、現代の時間や角度の計測方法に引き継がれています。
オブジェクト志向プログラミングにおけるクラス(名前空間)設定においても、「関心の分離(絶縁)」がきちんとした形で設計に盛り込めないとカプセル化による疎結合高凝集が実現出来ず密結合(コーディングにおけるスパゲティ状態)が発生してしまう訳で、N進数の位取りの様に機械的に「秒単位の事象」「分単位の事象」「時間単位の事象」を割り振る60進法の発想は大いに参考になるはずです。いわゆる「コクピット経営論」においても「ミクロコスモス的事象とマクロコスモス的事象の連続性確保」は重要な課題であり、こういう方面でもe進数(ネイピア進数)概念の応用が期待されるという次第。
60進数は物理的乱数発生装置としても優秀な側面があるらしく、現在は大体52枚前後で落ち着いているトランプも大元は13枚の大アルカナカードを加えたタロットカードだったといわれている。おそらく歴史のどこかの時点で「65枚は多過ぎる」的判断が勝って現在の枚数に。

「統計学者が確率計算の結果生み出した」トレーディング・カードゲームのマスターピース「マジック・ザ・ギャザリング(MTG=Magic: The Gathering,1993年~)」も1デッキ60枚を基本とする。
そんな風に視界が開けてきた時点で以下続報…
