
【*】神話論理は表層四項、深層四項の八項関係で世界の起源を分節する -レヴィ=ストロースの『神話論理』を深層意味論で読む(67_『神話論理3 食卓作法の起源』-18)
クロード・レヴィ=ストロース氏の『神話論理』を”創造的”に濫読する試みの第67回目です。『神話論理3 食卓作法の起源』の第三部「カヌーに乗った月と太陽の旅」の最後のところを読みます。
これまでの記事は下記からまとめて読むことができます。
これまでの記事を読まなくても、今回だけでもお楽しみ(?)いただけます。
レヴィ=ストロース氏は『神話論理』で神話を分析する目的について次のように書いている。
「生のものと火を通したもの、新鮮なものと腐ったもの、湿ったものと焼いたものなどは、民族誌家がある特定の文化の中に身を置いて観察しさえすれば、明確に定義できる経験的区別である。これらの区別が概念の道具となり、さまざまな抽象的観念の抽出に使われ、さらにはその観念をつなぎ合わせて命題にすることができる。それがどのようにして行われるかを示すのが本書の目的である。
神話は「経験的区別」を「概念の道具」として「抽象的観念」を抽出する。
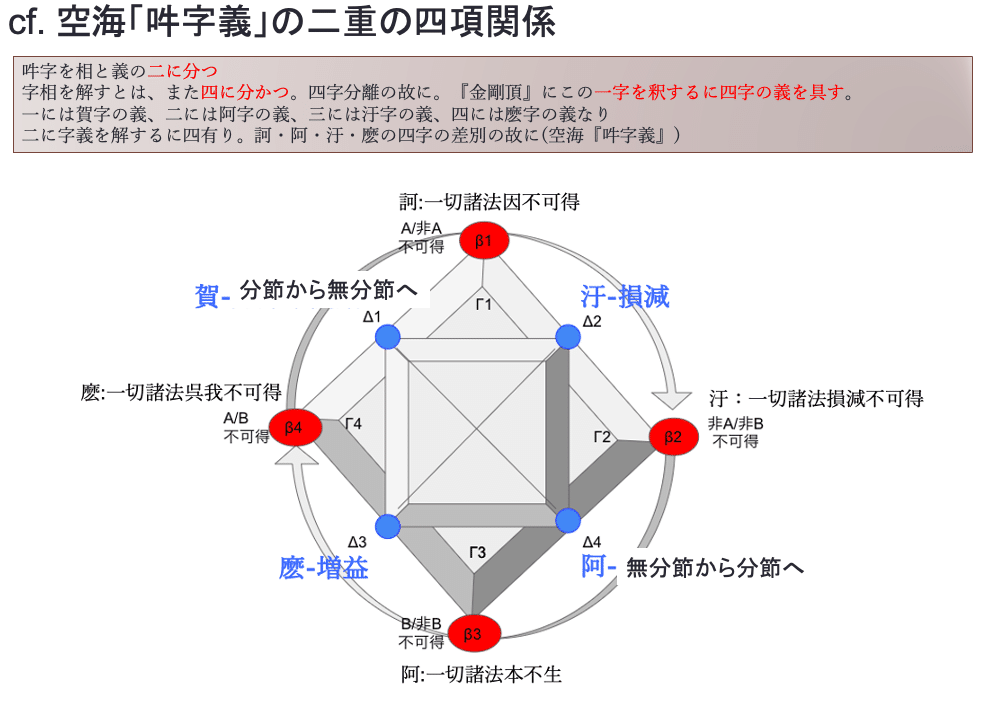
これまでの一連の記事では、レヴィ=ストロース氏が南北アメリカ先住民の神話分析を通じて浮かび上がらせようとしている「神話の論理」を、空海が『吽字義』に記しているような二重の四項関係(八項関係)の曼荼羅状のパターンに照らし合わせて読んできた。

すなわち、神話は、語りの終わりで、図1におけるΔ1〜4を分けつつ、過度に分離しすぎない、安定した曼荼羅状のパターンを描き出すことを(仮に)目指している。
そのためにまずβ二項が第一象限と第三象限の方へとながーく伸びたり、β二項が第二象限と第四象限の方へとながーく伸びたり、 中央の一点に集まったり、という具合に振幅を描く動きが語られる。
お餅、陶土、パイ生地を捏ねる感じで、四つの項たちのうち二つが、第一の軸上で過度に結合したかと思えば、同時にその軸と直交する第二の軸上で過度に分離する。
そしてこの分離を引き起こす軸と結合を引き起こす軸が高速で入れ替わっていく。
*
そこから転じて、βたちを四方に引っ張り出し、 β四項が付かず離れず等距離に分離された(正方形を描く)ところで、この引っ張り出す動きと中央へ戻ろうとする力とをバランスさせる。
ここで拡大と収縮の速度は限りなく減速する。そうしてこのβ項同士の「あいだ」に、四つの領域あるいは対象、「それではないものと区別された、それではないものーではないの」たちが持続的に輪郭を保つように明滅する余地が開く。
ここに私たちにとって意味のある世界、 「Δ1はΔ2である」ということが言える、予め諸Δ項たちが分離され終わって、個物として整然と並べられた言語的に安定的に分別できる「世界」が生成される。
何らかの経験な世界は、その世界の要素の起源について語る神話はこのような論理になっている。
もちろんこの世界は、βの振動数を調整し、今ここの束の間の正方形から脱線させることで、別様の四項関係として世界を生成し直すことも決してとどまらずに続く。
* *
神話論理のこのような読み方については、哲学者の清水高志氏の『空海論/仏教論』や、中沢新一氏の『構造の奥』の第一章などが導きになる。
ところで、レヴィ=ストロース氏は図1のような図を『神話論理』に掲載したことはないし(のちの『仮面の道』になると、近いものが登場してくるのであるが)、βとかΔいう用語もこの記事を書いている私が勝手にやっていることで、レヴィ=ストロース氏が書いたものとは関係がない。
とはいえ、しかし、なんと。『神話論理3 食卓作法の起源』の第三部「カヌーに乗った月と太陽の旅」215ページから222ページまでを読むと、そこには次のような言葉たちが並んでいる。
分離と結合を隔てておきながらかつ交わらせる
二項を互いに対立させる
静的な対立から動的な対立へ
これは!
という感じである。
例えば、次のようにレヴィ=ストロース氏は書いている。
「換言すれば、カヌーの神話素は、結合と分離の存在を明確にし、双方を隔てておきながら、かつ交わらせている。これらの論理的操作は、結合と分離の双方を同じ意味論的領域に維持しつつ、双方にそれぞれ中庸の値をもたらしている。」
分離と結合を分離しつつ結合し、結合しつつ分離する。
あるいは、分節と無分節を分けつつ繋ぎ繋ぎつつ分ける。
またレヴィ=ストロース氏は次のようにも書いている。
「要するに、対立という性格を維持していさえすれば、太陽と月の対立は何であれ意味しうるのである。神話的思考は[…]たえず新たな対立を発見していくが、そういう新たな対立により、べつの対立を言い表すさいにすでに用いていた用語同士の等価性を認めざるを得なくなる。」
分離と結合の分離と結合を通じて分離されたり結合されたりしている”諸項”たちは、なんでも良いし、何と入れ替わる=置き換えられる(=意味する)こともできる。
分離するということは差異、つまり異なるということ=異質発生することであり、分離しない(結合する)ということは同一性が、同質が発生するということである。
分離 ></>< 非-分離
||
差異 ></>< 同一性
||
異質 ></>< 同質
ここでこの対立関係の両極が結合したり(非分離)、分離したりしているところでは、ある何かでもって他の何かを表す=意味するということ、ある何かを他の何かに置き換えることである「意味する」という動きは、”全てが全てを意味しうる”潜在的な可能性にまで励起されている。
またレヴィ=ストロース氏は次のようにも書いている。
「カヌーでの旅という図式は[…]異なる段階でとりあげられたさまざまな対立を総合し、内部のそれぞれ対立する各項がひとつの新たな対立を形成するような体系からなる包括的産物を生み出す。」
レヴィ=ストロース氏が書かれている言葉が、対立関係の対立関係の対立関係としての二重の四項関係(八項関係=密教の曼荼羅)に急接近して来る。
なんとおもしろいのだろう。
+ +
二項対立を分節するβ脈動に
周波数変調をかけたり、振幅変調をかけたり
『神話論理3 食卓作法の起源』p.199からの神話「M104 夜の起源」を読んでみよう。
太初、夜は存在しなかった。
太陽が絶え間なく行き来して、人間は働かずに昼間眠っていた。
*
ある日
川にいたひとりの男が、水に棲む精霊に連れ去られそうになった。
その様子を3人の「無分別で反抗的な」娘たちが目撃した。
3人の娘たちは男を助けようと川に近づいた。
水の精霊は怒り、3人の娘たちを川に引き摺り込んだ。
そして助けに駆けつけた他の村人たちもつぎつぎと川に落ちた。
河岸には3人の老女だけが残った。
3人の老女たちが遠くから様子を見ていると、男が3人の娘のうちの一人を助け出て浮かび上がってきた。そして男は助けた一人目の娘を老女たちに預けると、あとの二人の娘も探しにいく、と再び川に戻っていった。
*
このとき、3人の老女たちは、助けられた一人目の娘に対し、あの男に惚れたと思うが、くれぐれも結婚しようなどと思わないように、遠くに逃げるように、と言った。「あの男は結婚をしない男なのだ」と「私たちも彼との結婚を望んだが、放置されたまま老人になってしまった」と。
娘は話を聞いたが返事をしなかった。
その間、男はあとの二人の娘を助けようとしていたが、彼女たちはもう、男の声を聞くことはできなくなっており、ついに水中に没していった。
*
男は悲しみの涙を流しながら岸にあがってくる。
すると、唯一助けた娘も泣いている。
男が娘に対して涙の理由を聞くと、自分もまた3人の老女のようにあなたと結ばれずに一生苦しむことになるのだろうか、という。
男は、そもそもあの3人の老女は自分の恋人ではないと抗弁した。
それに対して老女たちは、男が結婚に無関心であることを非難した。
そして老女たちは、娘に襲いかかると髪の毛をすべて引き抜いた。
たまらず娘は川の中へ飛び込んで逃げる。
男もそのあとを追って川に飛び込む。
老女たちはオポッサムに変身した。
(続く)
はじまりは昼/夜の区別が未分、太陽だけが常に地上を照らし熱する「暑すぎる」未分離・未分節の世界である。
この時点でもう「ああ、ここから、四つの登場人物たちが過度な結合と過度な分離の両極のあいだを行ったり来たりする話になるんだろうなあ」と推定ができる。
まず「水に入る地上の男」・・β1
そして「水に棲みながら地上の者を引っ張り込む精霊」・・β2
そして「3人の無分別な娘たち」 ・・β3
そしてそして「3人の老女たち」・・β4 である。
まずβ1とβ2、男と水に棲む精霊が、過度に結合しようとする。
このβ1とβ2を引き離す=分離すべく、β3(3人の娘たち)がβ1とβ2がもつれ込んでいるところに結合する。分離するために結合する、という分離と結合という対立する二極が一つに重なってしまっていることに注目してほしい。
前回の記事で取り上げた神話の大洪水と同じような場面から順番に神話的人物たちが浮上してくる。
+ +

分離したら結合し、結合したら分離する
高速ββββ脈動
あちらを分離するために、こちらで結合する。
こいうのをβ脈動と呼ぶのであった。
ここでβ項同士の分離しているところと結合しているところの組み合わせが切り替わる。
まずβ1男は、β2水の精霊とは「分離」することに成功する。
β1男はこの分離から転じて、β3「3人の娘」のうちのひとり、3人の娘を二グループに「分離」したうちの一人の方と結合する。
対する水の精霊β2はβ1男と分離したのち、3人の娘β3を二グループに分けたうちの二人の方と過度に結合する。
3人一組だった娘たちが二グループに分離され(2と1)、一方がβ2と、他方がβ1と、結合する。
ここでまたβ項同士の分離しているところと結合しているところの組み合わせが切り替わる。
この辺りはあまり細かいことには拘らず、こちらで分離するとあちらで結合し、あちらで結合するこちらで分離する、何とも忙しいなあ、という具合に眺めておけば良い。
そして男β1は助けた娘β3の半分を、岸辺の三老女たちβ4に託す。
β1とβ3の半分とβ4が結合したところから、β3の半分とβ4が結合したまま、β1だけが分離する。
ここでβ4三老女たちは娘に言葉を吹き込み、娘を自分たちと「同じようなもの」にしないために、β3娘の半分ををβ1男からよりさらに遠くへ分離しようとする。
しかし、β3の半分である娘はβ4の言葉には耳を傾けず、その場を去らず、帰ってきたβ1男と改めて「結合」状態に入る。ここで男は娘を配偶者として選ぼうとし、その間を引き裂こうとする老女たちを非難する。β1男とβ4老女たちの「分離」が決定的になる。
ここでβ4老女たちはβ3娘たちの「半分」である一人残された娘の「頭の毛をとる」という形で、彼女をさらにまた「二つ」に分ける。半分の半分、四分の一になったβ3娘は、髪の毛を老女たちにくれてやって、そして自分はβ2水の精霊の領域へと過度に結合していく。β1男もあとを追って、せっかく分離したβ2「水」の中へまた結合しにいく。

この神話のβ四項の分離と結合の速さは目を見張るものがある。
++
Δ四項の分節モードへの変換
ここで一足先にβ4老女たちがβ項たちが過度に結合したり分離したりする関係から離脱して、「オポッサム」というΔの位置へと向けてずれ始めていく。老婆たちが「変身」している、文化的な老婆でもあり野生動物のオポッサムでもある存在はβでありながら、今ここではΔ領域へとずれ始めている。こういう移行というか変換というかが神話論理の肝である。
つづきをみてみよう。
男は水中を泳いで逃げる娘を追いかける。
すぐ後ろに追いつき、踵にさわれるまでになったが、娘はさらに泳ぎ続けた。泳いでいるうちに彼女の髪は真っ白になった。
泳いで逃げる娘と、彼女との極めて近い距離保ったまま、彼女と同じ速度で泳いで追いかける男。この不思議な泳ぎは5ヶ月続いた。
その間、男の方も次第に髪の毛を失っていった。
そしてついに、二人はある岸辺にうちあげられた。
男は娘に、なぜ逃げるのかと問う。
娘は男に「髪が白くなるのが怖いからだ」と答える。
髪なんて・・と言いつつ、ふと自分の頭に手をやると男は自分の髪がなくなっていることに気づき、水の精霊に文句を言う。
娘は男に、自分たちはもうこの姿で生きていくしかない、と言った。
男は、俺は故郷に帰っても、むき出しの頭を情婦たちに嘲笑われるだろう、と嘆く。そして男は娘に「ぼくの髪が生えるようにしてくれよ」という。
娘は男に「私の髪を黒くしてよ」という。
この不毛な議論をつづけながら二人が一緒に歩いていると、無人の家に辿り着いた。その家に残されていた食料を二人が食べていると、そこに娘の両親が現れた。この家は娘の両親のものだったのである。
両親は髪が真っ白になった娘を娘と認めず、訝しがる。
また、禿げ上がった連れの男を嘲笑った。
その後両親は娘を認め、その伴侶となる男を認め、二人の白髪と禿を治す秘訣を例の三老女ならば知っているのではないかと思いつき、四人で三老女のもとに帰る旅にでた。
*
ようやく老女たちの小屋に辿り着いたが、そこはすでに三匹のオポッサムの巣になっており、ひどい悪臭がしており、とても中に入れなかった。
男は小屋ごとオポッサムどもを焼き払おうと火をつけた。
強烈な焼けこげの匂いが広がった。
娘はその匂いを嗅いで、老女たち=オポッサムが小屋の中に隠しているはずの自分の髪の毛が燃えている!と男に抗議した。
その途端、陽の光は消え、深い夜の闇があたりをつつんだ。
そのとき、火の熱によりオポッサムたちの目が破裂した。
そして飛び出した火花が空に舞い上がり、天に落ち着いた。
男は燃え盛る小屋の中で娘の髪の毛を探そうと格闘し、娘とその両親もあとを追って燃える小屋の中に入っていった。そして、四人とも焼き尽くされたが、彼らの体は破裂し、天空まで飛ぶ。彼らの燃えさしが、夜の空を飾ることになった。
(おわり)
β3の四分の一娘とβ1男がつかずはなれずの等距離を保ちながら川を泳ぎ続ける姿は、カヌーの先端と後端にのった月と太陽の関係とおなじである。二人が同じ速度で距離を保ちながら川を進むとき、二人の間の相対的な距離を変動させる分離ないし結合へと向かう速度は0のままになる。
β脈動する二人は”分離するでもなく結合するでもない”、第四レンマ的な関係にありながら、同時にその間の「距離」が一定に定まる。ここでつまり、βモードでありながら、その速度の同一性ゆえの距離の一定性が確立されるのであり、ここから世界が発生する。ここはカヌーの神話でもそうだが、神話論理の極めて精妙で絶妙、おもしろいところである(相対性理論におけるローレンツ変換が確かこう言う話だったような)。
さて、この泳ぎの途上で、β1男もまた「髪の毛を失う」つまり半分になる。
β項を「半分にする」とは、β項が描く振れ幅の両極がそれぞれ際立つということであり、これがΔ領域を定常化させる焦点になる。
往路の旅と帰路の旅の対立
この不思議な長期間にわたる「泳ぎ」がようやく終わる。
川β2から分離し毛を失って半分になった男(β1)/2と、四分の一になった娘(β3)/4は、あれこれ口論しながらも一緒に歩いて旅をする。
仲良く一緒に旅をするのではなく、あれこれ文句を言い合いながら一緒に歩む。これは引き続き、単に一緒にいる=結合しているのではなく、付かず離れずの状態、分離しつつ結合し結合しながらも分離するβモードにあることを示している。
*
そして二人はβ四分の一娘の両親のもとへたどり着く。
おもしろいのは当初両親は娘とその連れの男を歓迎しなかったが、しかし一緒に、四人で旅をしてオポッサムに変身した老女たちβ4のもとへと帰ってくる。
この、歓迎していないのに、一緒に旅をする、というところもよくできている。この四人の関係も、分離しているのか結合しているのか、どちらか一方に決定しかねる不可得さをよく描いている。つまり四人は、綺麗に四分されているのでΔ四項関係と見紛うほどであるが、あくまでもβ脈動していると言うことを強調しておく必要があるのだろう。
星々の起源
オポッサムに変身した3老婆との再結合。
変容したβ4と、β1の半分と、β3の四分の一が、再びここで結合する。
そして燃え盛る小屋の中で彼が彼女らβ四項が渾然一体となって、β3の四分の一娘の、奪われた髪の毛の捜索がはじまるが、燃え上がる炎のなかで髪の毛は見つかるはずもなく、すべて一緒に燃え尽きて、破裂して天へと飛び散って、夜空に瞬く星々になる。
こうして”太陽が隠れて、星々が散らばって輝いている”という経験的な姿をした「夜」がはじまったのである。・・というか、
昼 / 夜
が対立しつつ規則的に交代する秩序がはじまったのである。

*
昼夜という、規則的に交代するΔ二項の対立関係を区切り出すために、四つのβ項たちが、こちらで結合しあちらで分離し、あちらで結合しこちらで分離し、という動きを繰り返す。
β四項たちの分離と結合の分離と結合の動きで興味深いのは、この運動の大枠を二分する速度の違いである。すなわち、低速での往路と高速での復路の対立である。
行きは低速、帰りは高速
1)5ヶ月にわたる長期の水中移動の旅と、高速で戻ってくる陸上の徒歩の旅とを組み合わせた「跛行的」な行程
2)「規則的に」交代する昼夜をつくる天体の運行行程
この1)と2)が、みごとに対立していると、レヴィ=ストロース氏は指摘する。1)短い波長と長い波長が交互に訪れる「跛行的」なリズムと、2)等間隔で訪れる強弱のリズム、この二つの差異である。
「規則的に交代する二者関係」とは、「規則的に交代する二者関係-ではないこと-ではないこと」である。「規則的に交代する二者関係」は「規則的に交代する二者関係-ではないこと」と区別され対立させられる限りで、それとして区切り出されてくる事柄である。
規則的に交代する二者関係 / 非-規則的に交代する二者関係
この右辺、「非-規則的に交代する二者関係」に当てはまるのが、5ヶ月にわたる水中の往路とあっという間の陸路の復路からなる、いわば周波数変調をかけられた二極間の振動である。

ここでレヴィ=ストロース氏は次のように書いている。
「ところで、いまや奇妙な事実を確認せねばならない。ここで引き合いに出した神話すべては、天体と人間の結婚の結果である栽培植物にせよ、かついてはあまりにも近づきすぎていた太陽と大地のあいだに割って入って双方を引き離した料理の火にせよ、あるいは、いついかなる場所でも分離の結果として生じる生の短さにせよ、天と地の関係にかかわりがあるのだ。それらの神話では太陽と大地の関係がつぎのふたつの方法で捉えられている[…]。すなわち、料理の発見により家の竈が天と地のあいだに介入した結果断ち切られた垂直的で空間的な結びつきという形で、あるいは、生と死や昼夜の規則的な交代の導入により断ち切られた水平的で時間的な結びつきという形で捉えられている。」
天と地の関係、天/地の分離と結合のバランスが、神話論理の八項関係を分離しつつ結合する軸を発生させる。
語りの冒頭で天/地が離れていたとすると、その「結合」から、「栽培植物」という、”自然のものでありながら人工のもの”という、野生と文化の中間のような経験的項が占めることのできる領域が開かれる。
天体>>(結婚)<<人間
↓
栽培植物
語りの冒頭で大地と太陽がくっつていたとすると、その分離は、”天の火(太陽)とよく似たようなものであるが人間のものになった料理の火”という、これまた中間的な経験的項が収まる領域を開く。
太陽<<(近すぎ)>>大地
↑
あいだに割って入って双方を引き離す料理の火
天/地の区別が、過度に結合することなく、適度に付かず離れずにする。天地が過度に結合していると、焼け爛れ、荒廃した地上世界になってしまう。天地が過度に分離していると、長い夜の混沌が地上を覆い尽くす。
過度に結合でもなく、過度に分離でもない、適度に分離しつつ結合した「調停」された天/地の二項関係を分けつつつなぐときに、その媒介を一身に引き受ける媒介として「かまど」の「料理の火」や、「先端と後端にひとりづつ乗ったカヌー」といった項が呼び出されてくる。
「長旅の時間の間、月と太陽、夜と昼とを、それぞれ適切な距離を置きつつ結びつけているカヌーは、家族の小屋という形で区切られた空間における、家の竈のそれに匹敵する役割を果たしているのである。」
この際、分離しつつ結合する媒介の方向に、垂直方向と水平方向の区別がある。
料理の火・竈は、天と地のあいだを垂直方向で距離を適度に分離する。
太陽と月がのったカヌーは、生/死や昼/夜の規則交代により、時間軸上で天/地(太陽と大地)を適度に分離する。
区別がつかないほど一つに結合したり、
並立不可能なほど鋭く対立したり
ここでレヴィ=ストロース氏はM424「禿の起源」という神話を紹介する。
大昔、大洪水が人間を滅ぼした。
大洪水を引き起こしたのは、海の主である大蛇だった。
わずかな人間が食料を背負って、洪水と暗闇を逃れて三つの峰をもつ山に登った。
この山の主は別の大蛇だった。
山の大蛇は海の大蛇と対立していた。
山の大蛇は貧しい翁の姿に変身して、あらかじめ人間たちに危険を知らせていた。
歩くのが遅かった人々は、逃げ遅れ、魚に変身した。
残りの人々が山に登ると、山がさらに高くなって彼らを水から守った。
しかし、山が高くなりすぎ、太陽に近づきすぎて、人々は焼かれるようであった。たまらず頭に皿をかぶって日除にしたが、多くの人は焼け死んでしまい、生き残った数組の夫婦も頭が焼けて禿げてしまった。
二匹の蛇は長い間、戦いを続け、ついに山の蛇が勝利した。
生き残った人々は人身御供をささげ、水位を下げて、山から降りた。
そしてまた地上に人間が溢れた。
神話の最後で、人間が暮らすことのできる地上の世界、天/地が適度に付かず離れずに分離された距離が区切られる。
適度に分離しつつ結合している必要がある。
この適度な分離と結合に至るまでに、四つのβ項が、区別がつかないほど一つに結合したり、並立不可能なほど鋭く対立したりするように動く。そして直交する二軸を引くようにして、最大の振幅と最小の振幅を描く。
β1・・海の蛇
β2・・山の蛇
β3・・魚に変身した人間たち
β4・・溺れずに山頂に移動した人間たち(のちに禿げる)
仮に、このようにおいてみよう。
β1海の蛇とβ2山の蛇は鋭く対立し、並立することができないほど過度に分離=距離を広げようとする。しかしこの対立の過程で、山が海に飲み込まレそうになる、という具合に過度に結合する。
β3魚に変身した人間たちとβ4山で禿げる人間たちはもともと区別なく、一つになって一緒に行動していたところを、山を登る速度の違い(遅い/速い)によって分離される。
β1海の蛇と、β3魚に変身した人間たちは、もともと分離していたところが過度に結合するよう急転換する。
β2山の蛇と、β4山で禿げる人間たちも、もともと分離していたところが過度に結合するよう急転換する。
ここからβ1海の蛇とβ2山の蛇との勝負がつき、両者の間の距離が確定され、β山から垂直方向(上)にずれたところに”Δ天”が、β山から垂直方向(下)にずれたところに”Δ地”が、広がることになる(そして水界は山の地上と一連のものになるのだろう)
またβ4山で禿げる人間たちも、Δ山から地上に降りて今日の人間たちにつながる者たちと、Δ人身御供になったものたちとに分離する。

レヴィ=ストロース氏は書いている。
天と地が過度に分離してしまうと「腐敗した世界」になる。
天と地が過度に結合してしまうと「焼けただれた世界」になる(p.211)。
「諸神話はこのテーマを、言うなれば、おのおのがそれぞれひとつの意味合いを通過させるようないくつかの帯域の上で回析させているかのようだ」
経験的で感覚的な対立関係において、過度な結合へと向かう動きを示す二項対立と、過度に分離しようとする二項対立を、集めていく。そうしていくつもの対立関係が「あらゆる対立は、したがって、識別可能な構造を持つ網の目の上に配置される」ということになる(p.212)。これを表現するのがp.213に掲載された図16である。
網の目構造

この網の目は、ぐにゃぐにゃと動いている。どこか端の方を二箇所つまんで引っ張れば「線」のようになるだろうし、こねて丸めれば、一点に凝集したようなボールになる。
この網の目の結び目を、いずれか四つ、引っ張り上げて結び合わせて、その結び目を固定するように他を編み直すと、最小構成で八項関係を組んだ場合に、うまい具合に等距離に四つの結び目が分離されたような状態になるはずである。
「詰まるところ諸神話のあいだに見だされる相違点は、使用されている対立をそれら神話がどのレベルで引き出しているか、そして各神話があれこれの対を一致させることで、いくつかの対立同士の相同性を何らかの意味で明らかにすべく、いかなる独自のやり方でこの網構造を縦、横、あるいは斜めに折りたたんでいるか、に起因する。」
八項関係のモデルで神話の論理を記述してみる、というアプローチがレヴィ=ストロース氏の仕事に反するものではないことを論じる必要があるならば、この記述を引用して議論を立てたいところである。
*
ここで、レヴィ=ストロース氏は上の図16について「図示する必要から」複数の平面からなる網構造が「平たく単純化されてしまった」と注意を促す。
この網構造は動いている。
どの結節点も均一に同じ速度で動いているのではない。
速度には、遅いと速いの区別がある。ちょうど5ヶ月に及ぶ水泳と、徒歩での数日の旅との区別のように。
また、網構造の結節点同士の距離も、均一に固定しているのではない。
結節点同士の距離は、近づいたり、遠かったりする。この結節点同士の距離を引き離したり近づけたりする振れ幅から、時間軸(x軸)と、距離の軸(y軸)が浮かび上がってくるかのようである。

「ある軸から別の軸に移行するには、垂直構造を、他のあらゆる点で対応するような水平構造に重ね合わせるだけでは十分ではない。全体を部分へという位相的変形も達成する必要がある。ある媒介項によって結びつけられた両極からなる初めの体系が体系それ自体の媒介となる。」
この一文、「ある媒介項によって結びつけられた両極からなる初めの体系が体系それ自体の媒介となる」というのを、媒介項同士もまた二項対立関係を組むというアルゴリズムを加えて大真面目に組み合わせていくと、対立関係の対立関係の対立関係である二重の四項関係、八項関係が描ける。
「料理の起源に関する諸神話は、太陽と大地が両極となるような垂直軸を念頭においている。その両者のあいだで、料理の火の発見が中間項を出現させる。存在すれば料理の火は天と地の対立を媒介する。存在しなければ、両極は結合かあるいは分離かのどちらかを選ぶしかなくなり、結合からは、結果として昼の極端な表現である焼けた世界が生み出され、分離からは、夜の極端な表現である腐敗した世界が生じてくることになる。」
中間項に媒介されることによって、その両極は、付かず離れずに並立し続けることができるようになり、両極のどちらか片方だけになってしまう(過度に分離して、もう一方が遥か遠くにいなくなってしまう)ということが避けられる。
カヌーに乗った太陽と月
また、カヌーについても次のように書いている。
「カヌーは、相反する二極間にあって中庸の解決を担う媒体の役割を果たしている。そういう両極は、媒介項なしには直接の結合ないし分離によって消滅してしまうかもしれないのである。[…]ふたりの乗船者はどんな時でもたがいに接近しすぎるわけにはいかないが、共同の事業を遂行しているがゆえに、離れすぎるわけにもいかない。」
媒介される二項は、媒介されることで生成されており、媒介が止んでしまうと消滅してしまう。
+ +
「料理の火」や「カヌー」のような中間項は、経験的に付かず離れずのセットになっているはずの両極が、過度に結合して一つになってしまう事態を「遠ざけ」る。また、経験的に付かず離れずのセットになっているはずの両極が、過度に分離して、どちらか片方だけになってしまう事態も「遠ざけて」いる。
「いまや直面する問題は、各項のあいだの単純な対立ではなく、より複雑な、最初の対立を表現しうるようなふたつの様相のあいだの対立となる。この巻で取り上げてきた新たな諸神話は、項と項を対立させるにとどまらず、それらの項の相互対立が可能になる種々のしかたを対立させている。対立の諸形態をたがいに対立させることで判断論理から正真正銘の命題論理への移行を物語っているのである。」
対立の諸形態の対立。
項の相互対立が可能になる種々の”しかた”の対立。
最初の対立を表現しうるようなふたつの様相のあいだの対立。
この後者の方の対立もまた所与の事柄ではなく、振れ幅を描く動きを通じて結合したまま分離されて、分離されながらも結合を維持する。
分離と結合も二項対立
そしてこの分離と結合の分離と結合が、分離するでもなく結合するでもない状態をもたらすべき極めて基本的な二項対立が、他でもない、「分離」と「結合」の二項対立なのである。
「換言すれば、カヌーの神話素は、結合と分離の存在を明確にし、双方を隔てておきながら、かつ交わらせている。この論理的操作は、結合と分離の双方を同じ意味論的領野に維持しつつ、双方にそれぞれ中庸の値をもたらしている。」
「分離」と「結合」を、分離しながら(隔てておきながら)、かつ結合する(交わらせる)。そうして分離だけになることも、結合だけになることもないよう、両方を同時に保とうとする。
*
この分離と結合の二項対立を分離するでもなく結合するでもないようにするために、過度に結合しそうになったり、過度に分離しそうになったりしているある対立関係の両極の間を振幅を描きながらあちらからこちらへ、こちらからあちらへと動き回る媒介項たちが、神話の語りを先へ先へと進めながら、ぐるりと円環を閉じようとする。
対立関係にある二項については、このような動き方を示していることが重要である。
「要するに、対立という性格を維持していさえすれば、太陽と月の対立は何であれ意味しうるのである。神話的思考は、出発点において閉ざされた体系を形成する。[…]この思考はたえず新たな対立を発見していくが、そういう新たな対立により、べつの対立を言い表すさいにすでに用いていた用語同士の等価性を認めざるを得なくなる。」
対立関係にある両極は、別の対立関係と重なり合い、互いの項を置き換えあい、そうしてどの項も、他の項との対立関係から離脱して、そこから無関係に自足自立していることができない関係が脈動する。
ここで、経験的感覚的に対立しているA/非Aの両極さえもが「交換可能」にまでなる。対立されていることが必要であり、その対立の向きは、他の組み合わされる対立とのバランス次第でどちら向きでも良い、ということになる。
第三レンマ、第四レンマ
ここでレヴィ=ストロース氏は、分離と結合の両極の間で分離したり結合したりする二項の関係に、次の三つのパターンがあると指摘する。
まず「いっぽうか、他方か」。第一対立における分離と第一対立における結合を、第二対立における「分離」極と結合するとこれになる。
次に「いっぽうでも他方でもある」。第一対立における分離と第一対立における結合を、第二対立における「結合」極と結合するとこれになる。
そして「いっぽうでも他方でもない」第一対立における分離と第一対立における結合を、第二対立における「結合」極と「分離」極の両極の間で振幅を描くように脈動させると、これになる。
「いっぽうか、他方か」は排中律が効いている通常のロゴスの論理である。
「いっぽうでも他方でもある」は、第三レンマの論理である。
そして「いっぽうでも他方でもない」は第四レンマである。
* *
こうして神話論理は、”Aでもなく非Aでもない”第四レンマをその最も基本的な分離と結合の分離と結合のアルゴリズムにして脈動していることが、レヴィ=ストロース氏によって明らかにされるのである。
いよいよ本格的に、おもしろくなってきた。

関連記事
いいなと思ったら応援しよう!

