
蜂蜜の喪失から世界がはじまる -レヴィ=ストロースの『神話論理』を深層意味論で読む(34_『神話論理2 蜜から灰へ』-8)
クロード・レヴィ=ストロース氏の『神話論理』を”創造的”に濫読する試みの第34回目です。
これまでの記事はこちら↓でまとめて読むことができます。
これまでの記事を読まなくても、今回だけでもお楽しみ(?)いただけます。

この一連の記事では、レヴィ=ストロース氏の神話論理を”創造的に誤読”しながら次のようなことを考えている。則ち、神話的思考(野生の思考)とは、Δ1とΔ2の対立と、Δ3とΔ4の対立という二つの対立が”異なるが同じ”ものとして結合すると言うために、β1からβ4までの四つのβ項を、いずれかの二つのΔの間にその二つの”どちらでもあってどちらでもない両義的な項”として析出し、この四つのβと四つのΔを図1に描いた八葉の形を描くようにシンタグマ軸上に繋いでいく=言い換えていくことなのではないだろうか、と。
私たちが慣れ親しんだ日常の意味ある世界。あれがこれで、それはあれで、とみんなで同じような言葉で同じようなことをいつも一貫して意味していると信じて疑わずに居られるような「固まった」意味の世界。
それは「神話の論理」と呼ばれる仕組みから生み出され、支えられ、常に再生産されている。
人工空間が地球の陸地の表面を見渡す限り平定する以前、人間が人間の世界ではない世界(自然といってもいい)に取り囲まれ、人間のわずかな領分も、常に人間のものではない世界から脅かされ一瞬で飲み込まれそうな危機感とともに生きていたであろう古の人々にとって、日常と日常の隙間の節目節目に、神話的思考に触れることは大きな意味があったのだろう。
神話の論理と日常の論理
神話の論理と、非-神話の論理(日常の言葉の論理もこちら)、このふたつの、いちばんの「ちがい」はどこにあるのか?
*
大雑把な話で恐縮であるが、日常の言葉、非-神話の論理は、
AがBならばCである
X の意味はPである
If x>60 then print "Pass"
といった形をとる。中身のことは傍に置いて、形だけを見ると、
Δ1-Δ2-Δ3-Δ4-Δ5-Δ6-Δ7-Δ8- …
という具合である。これをΔ線形配列と呼ぼう(呼ばなくてもいい)。
言葉でも、変数でも、ある一つのΔの時間的・空間的「隣」に別のΔを置くことを繰り返していく。この順番に並べていくことを繰り返すと、Δ1-Δ2-Δ3-Δ4-Δ5-Δ6-Δ7-Δ8- …式のΔ項の線形配列が生じる。
このΔ線形配列の中で、あるΔが別のΔへ順番に置き換わって=変換されて=変身していくということが起きる。
りんご の 意味は 愛である
りんごの意味は・・・である
Δ1はΔ2であり、Δ2はΔ3である。
ここでふたつのΔはそれぞれ別々に異なったものであるが、しかし一列に並べられることで「異なったまま同じ」になる。もちろん、ただ並べればよいというものではなくΔの並べ方には構文というか文法がある。その規則に従って並べると効率よくあるΔから他のΔへ置き換えができる。しかし文法に従わなくても、ただΔをふたつ並べるだけで、第一のΔが第二のΔに置き換えられる(変換される・あるいは変身する)場合もある。
赤 とまれ
青 すすめ
それにしても一体どうして、言葉を二つを並べるだけで、二つうち前者から後者へ置き換え・変換・変身が起きるのか。
* *
例えば、リアルに「私」というひとりの人間がソファに座り、隣に猫が飛び乗ってきて座ったとしよう。
ソファの上で、「私」と猫が並ぶ。

ここで「私」が猫に変身したわけではない。
猫が隣に座ったくらいで、いちいち人間が猫に変身していたのでは、この世は犬派の人間ばかりになるだろう。
* * *
しかし、言葉になると事情が変わってくる。
言葉で「私」と「猫」を線形に、一列に、並べてみよう。
「私は猫である」
(吾輩 は 猫 である)
このように文を生成すれば、私(吾輩)と「猫」、ふたつのことがひとつであるという感じがしてくる。ソファに並んで座っているような経験的&バイオロジカルな猫は「吾輩は〜」と滔々と喋り出したりしない。「吾輩はねぇ」となどと滔々と語り始める者と言えば、バイオロジカルにはたいがい猫ではなく分別し切ったような顔をした人間であろう。この両者ははっきりと別々に分かれて、混じり合ったり区別がつかなくなったり変身しあったりすることはない。
しかし言葉で、私ーはー猫、とすると、「猫」が「吾輩は」と語っている、という感じがしてくる。「吾輩は〜」と語る者と猫というもの、ふたつがふたつのままひとつになる。

実に「意味深」に見える。
もちろん、AI生成画像それ自体が意味深なのではない。
この絵をみて「なにやら深い」「靴が片方脱げている意味は・・・」といいたくなる「わたしの「心(しん)」が、「深い」ところに果てしなくつながっているということである。
私は猫である。この文をよく見ると、私「と」猫ではなく、私「は」猫、と言っている。「と」と「は」の違い。英語で言うとbe動詞。
ここに語順における主語の位置と述語の位置の関係が、異なったものを異なったまま同じとすることの秘密を握っているということがよくわかる。
この、異なったものを異なったまま同じと「する」述語的な出来事を、Δ項目の線形配列の軸上に写像してみた、というのが、何を隠そう神話の論理なのである。
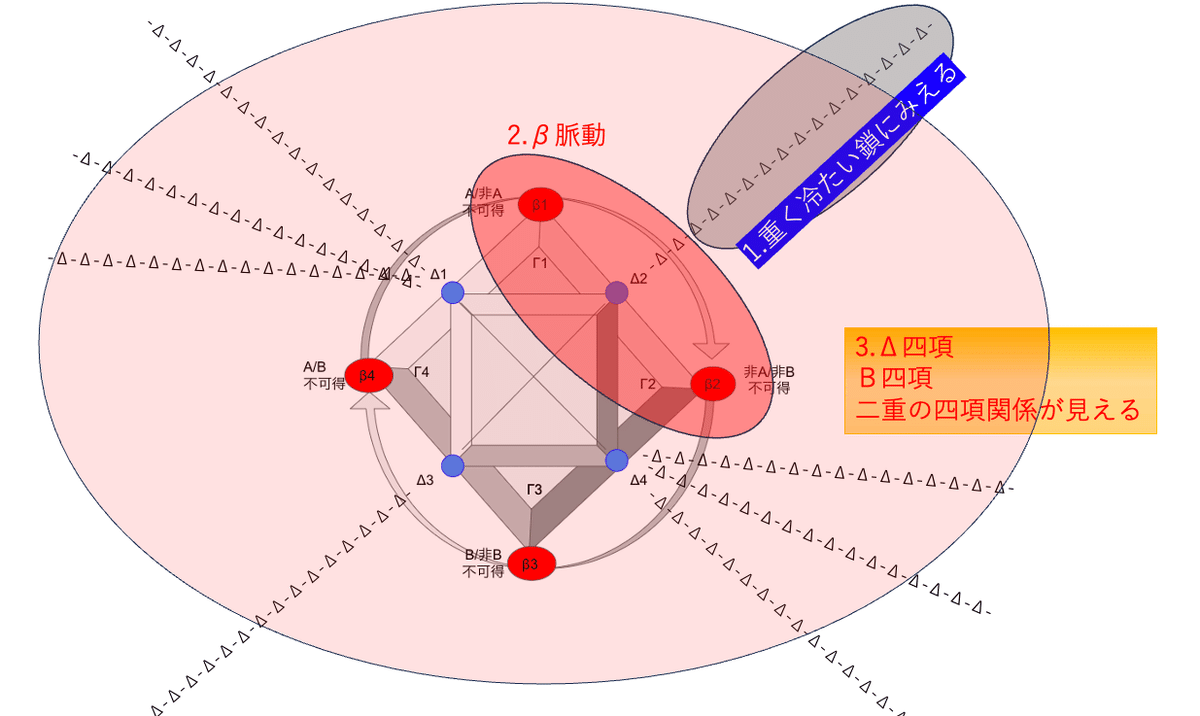
神話の論理は、異なったふたつのことを、異なったまま、同じひとつにする。
この神話の論理が、人間において、言葉やイメージ同士の意味するー意味されるの関係の手前で、「何かが何かを意味するということ」それ自体を可能にしているらしい。それはこの日常の、意味するものと意味されるものの関係がかっちりと固まっていつでもどこでも同じようになっているということの深層でもまた動いている。
神話の思考は「異なったふたつのことを、異なったまま、同じひとつにする」ような動き方をするものに非常に強い関心を寄せる。例えば、前回の記事で取り上げた「カエル」もそれである。
異なったふたつのことを、異なったまま、同じひとつにする。このことをまるごと象徴する「カエル」
カエルは、バネのように飛び上がり、下から上へ上がったかと思えば、上から下へ落ちる。さらに往々にしてカエルは、空気中=人間が呼吸して生きていられる世界から、水中へ=人間が呼吸して生きることはできな世界へと、ぽちゃんと水の音を立てて飛び込んだりする。
上に属するものか、下に属するものか。
水中に属するものか、陸上に属するものか。
上/下
水/陸
経験的に鋭く対立し、決して混じり合わない両極の間を、カエルはバネのように振幅を描きながら運動する。
バネのように飛び上がって落ちるカエルは、「異なったものを異なったまま同じと「する」述語的な出来事」そのことなのである。
*
バネ、特に板バネを考えてみよう。
板バネが振動すると振幅を描く。板バネの描く振幅の両極に、最大値と最小値が位置を取る。
板バネの振動のような述語。
音を立てて空中から水に飛び込む。
飛び上がって落ちる。
木の上に登る。
木の上から実を投げ落とす。
追いかけられた者が隠れる。

起源よりも喪失、あるいは起源は喪失のあとに
カエルは、上/下、水/陸、足のある動物/足のない動物 のような経験的な対立のどちらの極にも固定されない。
二項対立関係のどちらかの極に固定されないということ。
これが、神話の論理にとっては一番重要なことなのである。
*
このことは神話がものごとの「起源」について(その最たるものは人間が生きる人間にとって意味ある世界の「起源」だろう)語る場合に、もっとも鮮明になる。前回の記事でも引用したが、重要なのでまた引用する。
神話は[…]起源よりも喪失に関係している。最初は蜂蜜の喪失である。蜂蜜は元来いくらでも手に入ったのであるが、今では見つけるのが難しくなっている(M233-M235)。ついで獲物の喪失である。かつてはたくさんいたが、それが少なくなって散らばっている(M237-M239)。そして文化および文明の技術の喪失[…]。そしてついには、これらのどれよりも重要な、さまざまな論理的カテゴリーの喪失である。
p.295
あらためて「起源」よりも「喪失」というところに注目してみよう。
「起源」を問うこと。「起源」を考えることというのは、
起源→ Δt1-Δt2-Δt3-Δt4-Δt5-Δt6-Δt7-Δt8- …
Δ(t)線形配列を右から左へ、あるいは左から右へ、遡っていくことである。
人間というのは以前は猿で、その前はネズミのようなもので、その前は恐竜と共通の祖先をもっていて、その前は両生類的な何かで、その前は魚で、魚はの前は・・・。「起源」を語ることは、このような語り方になる。
ここで問題になるのは「どこまで遡るか」と言うことである。
あるいは、最初のΔの位置に、どの言葉を置くのか、ということでもある。
*
ここでひとつ、困ったこと(おもしろいこと)がおきる。
権利上、Δの線形配列は、無限につながっていくことができる。どこまでもまっすぐ伸びるのである。
なので、仮に誰かが「すべての始まりのΔはこれです」と、hyperなΔ項をぽんと置いたとしても、すぐに別のだれかが「そのΔの手前に、実は本当の始まり、Δ-1がありまして…」と言うことができる。
そしてまた別のだれかが「いやいや、Δ-1とおっしゃいますけど、その前にはΔ-2があって、Δ-1はΔ-2から流出したものですよ」などと言うこともできる。
Δの線形配列は、無限につながっていく。
しかし「起源」を「どこかひとつのΔに定めたい、定めたくて仕方がない!」という人にとっては、これは非常に具合が悪い。そこでやむを得ず「いいですか、起源はΔ0です。聞いてますか、Δ0より前に遡ることは禁止です。もしΔ0より前のΔに言及したらお口にガムテープを貼ります」ということになる。
*
神話が何事かの「起源」を語るとき、そのやり方は、Δ線形配列のアルゴリズムを用いてどこかひとつのΔの位置に「起源」という言葉を置くというやり方は採用しない。ではどうするのか?
始まり(主語的な)と始まる(述語的な)
神話の論理は、物事の「起源(はじまり)」をΔ線形配列の始端(終端)に位置する個物に求めようとはしない。もとより、Δ線形配列に「はじまり(主語的)」も「おわり(主語的)」もない。ないものを求めても仕方がない。
神話の思考は、Δ線形配列の「中」では動かない。
神話の論理は、Δ1-Δ2-Δ3-Δ4-Δ5-Δ6-Δ7-Δ8-のようなΔ線形配列が生成する手前にフォーカスする。
そして”異なったものを異なったまま同じと「する」述語的な出来事”を、あえてΔ線形配列である言葉を用いて、ぱっと見の見た目にはΔ線形配列以外の何ものでもない言葉でもって、観測し記述しようとする。下記の図でいえば、1.を転用流用、日常大工の材料のように降りコラージュして、2.のモデルを組み立ててみようとする。
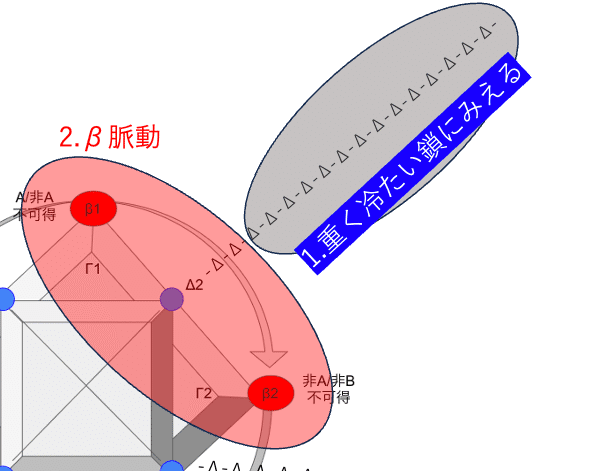
どういうことか、ひとつ神話をみてみよう。例えばM233である。
M233は、蜂蜜の起源を蜂蜜の喪失として語る。
かつて低木林にはミツバチの巣と蜂蜜がたくさんあった。
蜂蜜取りの名人の男がいた。
ある日、男が斧で木の幹に穴を開けていると、木の中から「私に怪我をさせないで」という女の声がする。
男が丁寧に穴を開けると、木の芯に美しい女がいた。彼女は自分の名前を「蜂蜜」であると名乗った。彼女は蜂蜜の精であった。
男は、綿を集めて蜂蜜の精に渡した。蜂蜜の精はその綿で服を作った。
男は蜂蜜の精に求婚した。蜂蜜の精は同意したが、「決して、人前で、わたしの本当の名前を呼ばないように」と命じた。
二人は幸せな夫婦となり長く暮らした。
夫は蜂蜜取りの名人、妻はマニオクのビールづくりの名人として知られた。
男はしばしば客を招いて宴会を開いた。
彼女がつくる酒はたったひと壺でも、全員が好きなだけ酔えた。
*
ある日、いつものように男が客を招いて宴会を開いていると、なぜかその日は、壺の酒を全て飲み干してしまった。男は客たちに謝ろうと「次はうちの妻、<蜂蜜の精>がもっとたくさん酒を用意します」と、彼女の名前を皆の前で言ってしまう。
たちまち、妻はミツバチに姿を変えて、夫の手をかいくぐって飛び去った。
このときから、蜂蜜は乏しくなり、見つけにくいものになった。
まず「かつて」蜂蜜はいくらでもあった。つまり、失われていない。
しかし今日現在、現に私たちが生きる世界では、蜂蜜は多くが失われ、貴重なものになった。今日現在の貴重品としての蜂蜜のあり方の「起源」が、かつての有り余る蜂蜜の「喪失」として語られる。
この蜂蜜の喪失に至る経緯を見てみよう。
まず有り余るはちみつの周囲で、いくつかの二項対立関係の両極が振動しはじめる。まず木の内/外、次に、男/女、そして文化(服を着る人間)/自然(服を着ない昆虫)の二項対立である。
内/外の間は「穴を穿つ道具=斧」によって分離されつつ結合される。
男/女の間は求婚と同意によって分離されつつ結合される。
そして文化/自然、人間/動物(昆虫)の間は、自然から獲得された綿で服を作るという操作において分離されつつ結合される。
複数の二項対立関係の両極(下図で言えばΔ項)が、両義的な媒介項・媒介作用(下図で言えば複数のβ項間の変換・変身・移動)によって、分離されつつ結合される。
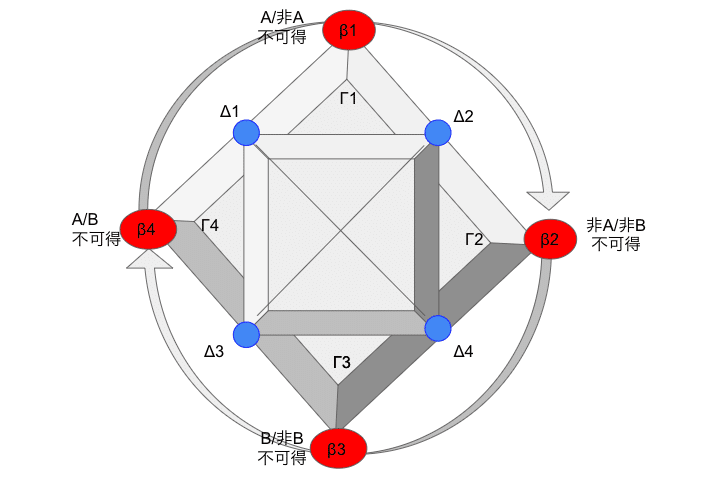
この高振動状態にあるあやうい結合(人間と昆虫のように、経験的感覚的には非常にはっきりと分離され、結合(結婚)したり、混じり合ったりすることはほとんど考えられないような関係を成り立たせているのが、一つの約束、「決して妻の名前を人前で言わない」という言葉の禁止である。
ある言葉を禁止すること。
言えるのに、言えない
「言えること」の膨大で広大な大海の中に、「言ってはいけないこと」が浮島のように浮かび上がる。ここに、ひとつながりでありながらふたつにわかれている、という分離しつつ結合する「線」のようなものが引かれる。この線のもとに内/外、文化/自然の対立が集められ、分離されつつ結合される、あやうくも幸せな均衡状態が訪れる。
例えば、内/外が分離されつつも繋がっていることの象徴が、「ひと壺しかないのに、いくらでも酔えるだけの酒が出てくる」という話である。この壺は内/外をはっきりと分けつつ、どうやらどこかの超空間かなにかに繋がっていて、無尽蔵に酒を汲み出すことができるようになっているらしい。
* *
ところが「ある日」・・・
神話で「ある日」とくると、なにやらゾッとする。
ある日、なぜか壺の酒が底をついてしまった。
超空間への通路が通じていてそこから無尽蔵に酒が湧いていたはずの壺が、もう、ただふつうの容器、内/外をはっきり分けて、決して混じり合わないようにするごく普通の経験的で感覚的な便利な壺になってしまった。
ここで夫がダメ押しの一言。
妻の名を言ってはいけないという禁止を、ついうっかりおかしてしまう。
内/外、文化/自然。通常は決定的に分離されて混じり合わない両極を、かろうじて結びつけてあやうい均衡を保っていたのがこの”言えるのに、言えない、昆虫でありながら人間の妻である者の名”であった。
いま、この「言えるのに、言えない・・・」の線が切れてしまった。
そうすると、内/外、文化/自然のあいだの危ういつながりは通路を失ってしまい、決定的にはっきりと分離され、混じり合わないようになった。人間の妻に変身していたミツバチは、ミツバチの姿に戻って飛んでいってしまい。無尽蔵に得ることができた蜂蜜も、ほとんど手に入らない貴重なものになった。
* * *
経験的に感覚的に私たちが慣れ親しんだこの世界、蜂蜜が貴重であるというこの世界は、「かつて」のすべてが重々無尽につながっていた世界の「喪失」として始まった。
ある何か「A」の「起源」について語る場合、Aは元を辿ればBから生まれ、Bは元を辿ればCから生まれ、Cは元を辿ればDから生まれ・・・、という具合に二項関係を順番に置いていくやり方をすると、どこかで疲れが出てくる。そうして「そもそも、最初の始まり、本当の起源は何?」という問いを問いたくなる。そうすると、「全ては元を辿れば、hyper-Xなんです」といった形で答えてみたくなる。ただこのhyper-Xも悩ましいところで、「hyper-Xのもう一つ前に、実はhyper-X-1があって・・・」という具合に、いつでもまた二項対立の置き換えが再開されてしまう。
「起源」に、”他からすでに区切られてある何か”を置いてしまうと、この因果の二項の無限の遡り、因果の二項の無限の置き換えが、止まらなくなってしまう。六道輪廻のアルゴリズムである。
ここで無限の遡りから脱するには、”何かが他から、区切られる”こと、そのこと自体に眼を向ける必要がある。
そこで神話における諸項の振動は次のような「循環的」な構造を描く。
二極からなる体系を、新たな項を持ち込まずに、循環的体系に変形している
あらかじめ区切られた項たちをどういう順番に並べましょうか、という話ではなく。まず区切ったから、区切るということ、分けるということが動くから、その後にあらゆる二項対立関係が生じ、あれこれの項たちが生じ、その後で、項たちをどの順番で並べようかという話もできるようになる。因と果、起源とその後の対立もまたこの「分けられた」一連の項たちのペアのひとつである。
「その後」に対する「起源」ということを語り得るようになるためには、まずそもそも「分ける」ということが動き始めていないといけない。この動き始めたばかりの「分ける」を捉えたのが、原初の無尽蔵の「喪失」である。
喪失は、最初のΔをΔ以前から分離する
なにごとか意味あることの起源を語るということは、つまりΔ線形配列が生成してくる述語的なプロセスを、言葉でもって記述するということであり、Δたちを使って、βの脈動をモデル化する、ということが求められる。
ここで「起源」よりも「喪失」である。
β脈動が、β項どうしが分離したり結合したり、一つになったりふたつに分かれたり、激しく振動している状態が止まり、いくつかの(最小ふたつの)β項が分離しきったか、結合しきったところにΔ項が生成する。
カエルがぽちゃんと音をたてて飛び込み、そしてこの音の余韻が尾を弾きつつ、やがて水面の波紋も消え、静寂が訪れる。カエルがまた水中から飛び上がってくることは(さしあたりは)ない。カエルが、水/陸の一方の極、「水」の中に包摂され、水とひとつになる。空気中に、空気の脈動としての「音」を残して。
* * * *
ちなみに、さきほどの神話は「鶴の恩返し」とそっくりである。
困っている鶴を、主人公のお爺さんは獲って食ってしまうのではなく、まるで人間相手のように丁重に扱って助ける。鶴は人間に変身して、人間の家に入り込み、自分の羽=自然物を材料にして文化の極みとも言える機織りをする。ただしその姿を「見てはならない」。この禁止を定めたところで、通常ははっきりと分かれている自然と文化が短絡し、無尽蔵に布が湧いてくる状況になる。しかし、「見てはならない」禁止をおかしてしまったために、鶴は飛び去り、布の無限生産はできなくなる。そうして布が貴重品であるような、今日現在の現実が生じた。
人間と、動物
自然(裸であること)と、文化(服(布)を作ること)
この経験的感覚的には鋭く分離された両極の間を短絡するのが「見ようと思えば簡単に見られるのに、見ることができない」という禁忌である。
そしてこの禁忌が破られたことで、人間と動物の世界の短絡路は閉じる。
さきほどの神話と鶴の恩返し。古今東西、計算したかのように(実際、人間の脳の普遍的構造?が”計算”したのだろうが)同じ展開がみられる。
ミツバチと人間が結婚?!
上の神話に続いて神話M235が紹介される。
ここでは、蜜蜂が男性/人間が女性の組み合わせで結婚が行われる。そして蜜蜂夫は運べないほど大量の獲物を狩猟してくる。
この幸せな生活は、妻の妹たちが義理の兄である蜜蜂夫に「水をかける」ことによって破綻する。
姉妹たちは、蜜蜂夫が他の男たちのように水浴びをしている姿を一度も見たことがなかった。彼は「水は、私の身体を火のように焼いてしまうのだ」と人々に言い、水浴びを拒絶し。誰にも見られないように、蜂蜜で体を洗っていたのである。妻だけはこの秘密を知っていた。
ある日、妻の妹たちが、彼に水をかけると、男は「熱い!」と叫びながら、ミツバチのように空洞のある木に飛んでゆくと、溶けて蜂蜜になった。そして蜜蜂夫と人間の妻のあいだに生まれた赤ん坊はカエルに変身した。木の上に住むカエルにである。
M235より
人間と蜜蜂の結婚において、
人間/動物(昆虫)
水/火
といった経験的にはっきり区別される対立が短絡され、一方が他方へ、他方が一方へと逆転するようなことが起きる。この短絡状態から、「浴びるほど大量の蜂蜜」や「運びきれない大量の獲物」が、自然界から人界へともたらされる。この、水と火を短絡してしまうほどのあやうい結合は、これまた「見ようと思えば見られるのに、見られてはいけない秘密」によって分離の相と結合の相の間で振幅を描く高周波の振動のようにして成立している。
これらの神話について、レヴィ=ストロース氏は次のように書いている。
「M235では、ミツバチが生きたまま川の水(大地の水)をかけられて死ぬ。この水はミツバチに対してまるで火のように作用する。ところで、チャコの神話では[…]キツネは、太陽の熱で死に、乾燥するが、雨つまり空の水で湿ると生き返る。チャコの神話では、キツネはキツツキと対立し、[…]チャコのキツネはギアナのミツバチと対立している。」
何と何とが対立関係を構成「しなければならない」というような規則はない。対立関係を規制するコードはあらかじめ用意されていないのだ。なぜならありとあらゆるコードはそれ自体がある固定された二項対立関係群によって定義されるのであるから、所与のコードのようなことを考えてしまうと、それはもうすでに二項対立を切り終わった「後」の世界の話になってしまう。
もちろん、人間の場合、前五識的な感覚神経系による言語的思考以前の分節(暑いとか寒いとか)が事実上のコードのように作用して対立関係を規制するが、それは残念ながらそうなっているという、それこそ「業」のようなもので、そうでなければならないというものではない。
対立関係を”分節する動き”は、その両極に何と何を区切り出しても良い。
ただし、この”分節する動き”と分節された二極は三者だけで関係しているのではなく、最小構成で八者(八項)で関係している。したがってある二項対立関係が何と何の関係になるかは、この二者だけの都合で決まるものではなく、八項関係の中の他の六項との関係で決まる。
「チャコの神話からギアナの神話へ移行する際に、変形がどれほど多様な軸でおこなわれているかが見えてくる。蜂蜜/獲物、男性/女性、生のもの/火を通したもの、配偶者/姻族、文字通りでの意味/比喩的な意味、通時態/共時態、乾いたもの/湿ったもの、上/下、生/死。この多様性が、この神話群の構成を直感的に把握するために、図表を利用するという希望を奪ってしまう。このような場合、図表の約束事が増えすぎて、説明を単純化するどころか、煩雑にしてしまうであろう。」
なかなか大変なことになっている。
図表の約束事が増えすぎて
ここでレヴィ=ストロース氏が「図表を利用するという希望を奪ってしまう」と書かれていることに注目しよう。この一言はよく読んでおきたい。
私は以前から、
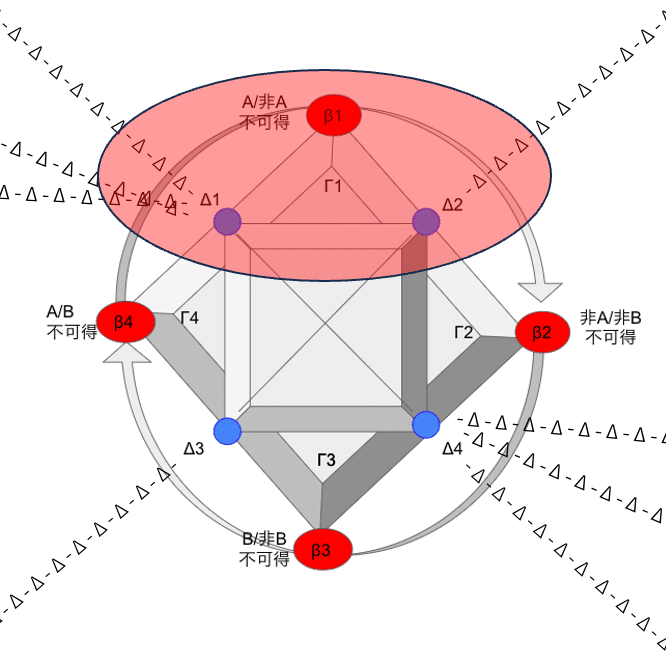
とか

のような図を示しては「こんな図を描くとレヴィ=ストロース先生に怒られるかもしれないが」などとたびたび書いてきたのはココである。
図表の約束事が増えすぎて、説明を単純化するどころか、煩雑にしてしまう
図表を利用すると、説明を単純化するどころか、図表それ自体についての説明と読み解き方の解説が次々と増えてしまい、かえって煩雑にしてしまう。
おっしゃるとおりです・・・
図を描いてしまうと、この図を、さらに言葉で説明するというくだりが必要になり、やれ「βは項として観察され記述されるが、項といっても個的実体ではなく、脈動であり、複数の脈動が干渉したところでその干渉波のパターンの様なものとして値が決まる」などと、自分で書いていても訳のわからないことを言い連ねることになる。
もちろん、個人的にはそういうのは嫌いではないので楽しんでいるのですが、こういうのが嫌な人は嫌だろうな、というのはさすがの私でもわかる。
*
しかしそうはいっても、実際この胎蔵曼荼羅の中台八葉院を参考にした「図」は、確かに追加の説明は必要になるのだが、「神話群の構成を直感的に把握する」上では役にたつと思うのである。
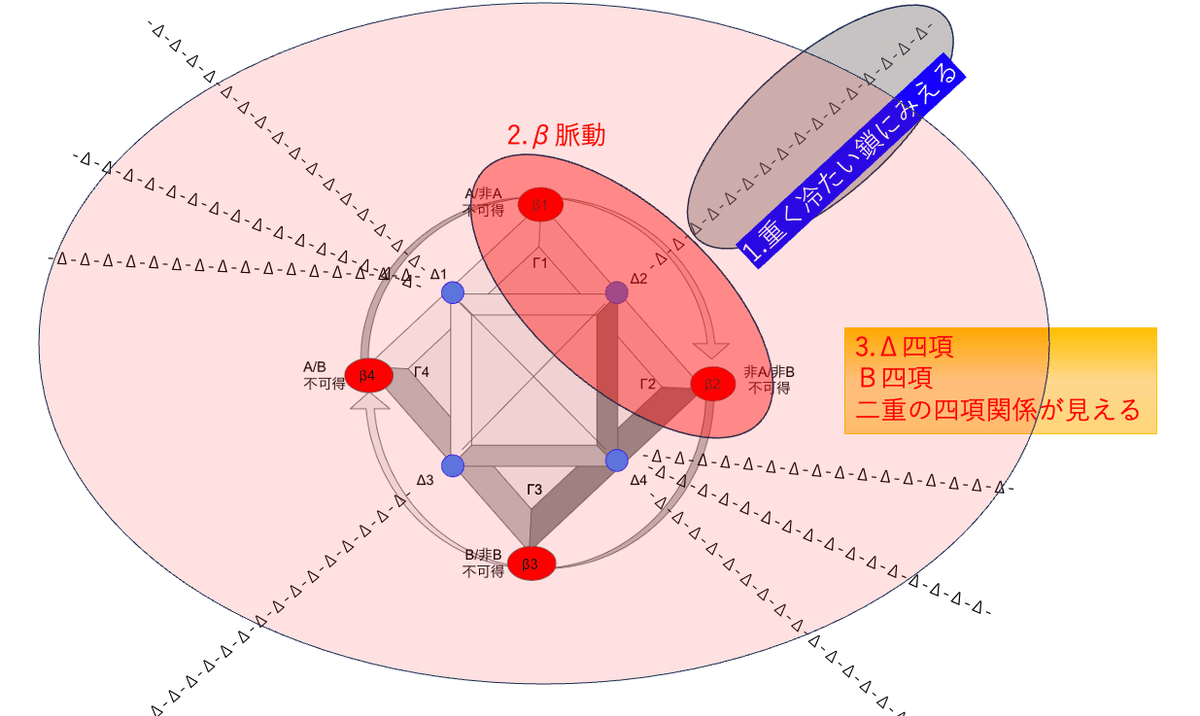
このような曼荼羅のパターンを描いていく(分節していく)アルゴリズムこそ「アサンメイ チリサンメイ サンマエイソワカ(超意訳すると”同じでないことと 三つが同じであることとは 異なりながらも同じことである”) 」の論理として記述できるものであり、これはつまり両義的媒介項から両義的媒介項へと次々と連鎖しては最少四つで円環をなす変身・変換の神話論理とシンクロする。
* * * *
神話は、β振動を、線形Δ配列に変換する。
神話は、線形Δ配列を、β振動に変換する。

何と何が対立するか。
対立関係の両極は、次々と変形(transform)されていく。そこに経験的区別が抽象的観念の体系へと転換する動きが起動する。
βと見ればβであるし、Δと見ればΔであるし
図は視覚的な分節システムであり、それこそ、ふたつの○を描くだけで、いや、点をひとつ打つだけで、そこに図と地が分節し、Δ線形配列がぞろぞろぞろと生成してしまう。
なので図を扱うなら、よく見切った上で、あくまでも仮のもの、として横に置いておくくらいがいい。
ここまで散々用いてきた下図で、一番煩雑というか、本来言わんとすることと逆のことを言っているように機能してしまうのは、βとΔという二種類の項があることだろう。
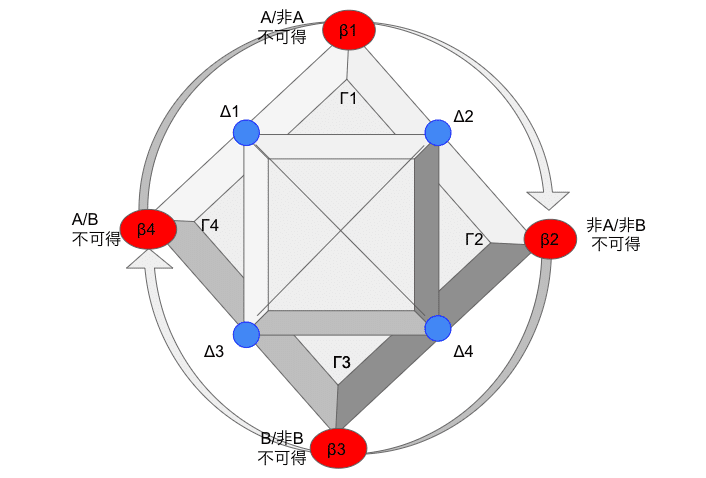
この図だけ、ぽんと与えられると、「項というものが八つあって、そのうち四つはΔという種類で、他の四つはβという種類なのだな」と思わせてしまう。
しかし、この図で言いたいことはそのようなことではない。
まず項は、それ自体としては、ない。
なんだと思われるかもしれないが、ないものはない。
ただし、それ自体としては「ない」が、両隣の項と三つ同時にドンと分節されることで、「ある」と観ることができるようになる。
次に、項は八つセットで固まったパッケージになっていなければならないというもの”でもない”。
項は最小構成で八つが一挙に分節するのであるが、あくまでもこれは最小構成なので、さらに増えてもよい。特に固定的に対立する両極の中間に位置をとる両義的媒介項の場合、その姿は次々と変身していくものであり、定まって固定した「一」であり続ける必要はない。

さらに、最小構成で八(もっと多数に変身、分身してもいい)のうち、実際に線形配列の言語に転写されて声に出されたり文字に記されたりするものが何個であるかは、まさに「方便」、語り手と聞き手の関わりの中で変化する。それこそ神話の論理を熟知している者同士が会話をすれば、二項に言及しただけで、自動的に語られていない残りの最少の可能性で六の項が想起されるであろう。
そしてβとΔについても、それ自体としてβ的、それ自体としてΔ的な項があるわけではない。
ある項をΔとして観測すれば、その両側は自動的にβに決まるし、ある項をβとして観測すれば、その両側は自動的にΔに決まる。Δかβかのちがいは、神話を語る言葉がどの語にフォーカスするかで、その都度、仮に決まる。人間の場合、前-五識的な感覚神経形による分節は対立する両極(暑いと寒いとか、上と下とか)をかっちり分けて、混じり合わないように固める傾向があり、寒/暖、上/下、前/後、明/暗、静/騒といった項はΔとして観測されやすいが、あえてその経験的にはっきりと分けられた対立を、次々と分離したり結合したり変身したりする項たちの振動のあいだで、はっきりと分けられないものに変換する。そしてこのはっきりとどちらか分けられないものたちの円環あるいは球体の一部が「喪失」するとき、そこで振動していたβ項がΔ項に変容し、Δ線形配列がはじまる。そこがいわゆるΔ線形配列の端としての「起源」になる。
レヴィ=ストロース氏は次のように書いている。
「わたしは、蜂蜜とタバコの対立から出発し、蜂蜜の起源に関する神話を描くさまざまな変形を、一歩一歩たどってきたのであるが、いまここで、わたしたちの世界が球形であることを発見しつつある。」
p.221
世界を記述する項たちは、何重もの円環を重ねた姿をしており、球体をなしている。通常の言葉の意味を成り立たせているΔ線形配列は、この球体から生えた毛のようなものだ。
神話では、二対の対立を構成する四項からなるシステムが、二項からなる対立関係が”交差する”様を盛んに提示する。そしてこの対立関係の対立関係にある四項が、神話の意味分節の最小の”システム”となる。

しかも、この四項関係は、それ自体として固まっている所与の項が、二次的に集まって構成する関係ではない。この四項関係では、関係が項に先行する。関係があって、その関係が動くことで(脈動といってもいい)その動きが残した波紋のようなものとして、はじめて「項」として観察しようと思えば「項」として観察できなくもない何かが浮かんでくる。
レヴィ=ストロース氏は次のようにも書かれている。
(一)連続する二つの神話において、動物の正体が同一である場合には、性が逆転する。
(二)連続する二つの神話において、動物の性が同一である場合には、種が「逆転」する。
これら二つの操作が相同であるということは、当然、ある動物から他の動物への変形は、必ず対立する対の中で生ずるということを、公理としてあらかじめ認めている、ということである。
二つの別々の神話、別々の二つの四項関係が問題になっている。
ある四項関係が、性別(雄/雌、男/女)の対立と、動物の種類の対立(例えば、キツツキ/キツネ、カエル/ミツバチ)という、二つの対立の対立で成り立っている場合、この二項対立を対立させる、いわば「向き」を逆にすることで、良く似た神話が、それでいて一方では主人公が女性だったのが、他方では男性になっているというような、一見「なぜそこを逆にするのか」と思いたくなるような変換が生じる。
A / 非-A
|| ||
B / 非-B
は、
A / 非-A
|| ||
非-B / B
に、変形される。
*
これは要するに、複数の二項関係をどちらの向きに並べてΔ四項の関係を組むか(そしてもちろんβ四項の関係を組むかも)二項対立関係の向きは自在に回転することができる、ということである。個々の二項対立関係は、特に人類という生命においては前五識的に混じり合うことができない両極に分かれているが、そうした二項対立関係を幾重にも重ねて「球形」を描いていく時、その重ね合わせる”向き”の自在さとして、人類の神話的思考は、動態にある意味分節する働きは、自由度、自在さを獲得するのである。
起源は喪失のあとに
ここで改めて「喪失」ということが鍵になる。
喪失ということは、かつてあった、が、いまはもうない、ということである。時間軸上の分節を一旦どこかに放り出しておけば、かつてあったといまないは同等である。あるがない、ないがある。
区別があるでもなくないでもなく。
あるのか、ないのか、はっきり分けるということは、
A / 非A
B / 非B
このような感じの二項対立が「二つ」、ポンと与えられているところで、AをBか、それとも非Bか、どちらに言い換えましょうか、という話である。
しかし、神話が問うている他でもない、ありとあらゆる二項対立の起源、始まり、即ち、二項対立があるでもなくないでもないところからの、二項対立の確定である。
この二項対立関係があるでもなくないでもない、二項対立関係があるとないの間で姿をゆらめかせる様子を言語でもってスナップショット的に描き出そうとする時「かつてあったが、いまはなくなった」式の語りが「論理的カテゴリーの喪失」の物語がピッタリとくるのである。
神話は閉じた体系である。こちらの図式に言い換えるなら、βからβへ、また次のβへ、β項どうしの逃げて隠れて追いかけて見つける分離と結合は、ぐるりと環を描く。互いにはっきりと分離されるわけではなく、放っておくとすぐにくっついたり、互いに変身しあったりするβ項は、一直線上に線形には配列されないのである。β項たちは、ぐるぐると遠回りをしようとも、いつでもどこでも、環状につながる。
*
この環状に連なったβ項たちのあいだに、不意に、「星になったもの」と「地上にのこされたもの」ほどの超遠距離の間隙が開く。
β項たちが多少動き回ったところで決して手が届かないほどに引き離される。
と、そこで初めて、Δ項目たちが、同時に四つづつ、混じり合わずに分離したままになる。そしてもちろん、分離はしているのだが、もともとは、遡ってみれば、βの相で繋がっていたのであり、いまでもつながっているのだけれども、それでも分離したままになる。
これがΔ線形配列の、その手前の「はじまり」「起源」である。

このはじまりは中間的で媒介的なβ項の振動状態、結合状態の「喪失」による。
β項が無限に連なる円環状の連鎖のうち、いくつかのβ項とβ項の連鎖が切れてしまい、その隙間を繋ぐものも失われる。
ちょうど「銛つき紐付きの矢」がそのβ媒介機能を喪失したように。
輪ゴムの一部を切り落とせば、一本の紐になる。
自在につながり合っていたβ項たちの環状の連鎖のなかに、容易に埋めることができな隙間が、距離が、ぽっかりと空いた時(つまりその部分の媒介的βたちが喪失したとき)、項たちの線形配列の生成が始まる。
つづく
↓↓↓つづきはこちらです
おまけ

今回もAIがなかなかよい曼荼羅を生成してくれた

ジブリの『君たちはどう生きるか』をご覧になった方などは、
ああ〜!!と思っていただけるのではないか。
Δ項をブリコラージュしてβ項をイメージ化すると、こうなるだろうな、という。
ちなみにわたしは、言葉でもってこういうこと↑をやろうとしているのである。

「項」の自律固定性みたいなものが完全に消えているのがいい。
印刷して、自宅の表札の上に貼りたいくらいだが、
それをするとおそらく家人が私の外出中に玄関の鍵を交換することだろう。
つづく
関連記事
いいなと思ったら応援しよう!

