
山本解析力学 §4 ハミルトン形式
§4.1 相空間
§4.1.1 Lagrange方程式の狭さ
ついにハミルトン形式に辿り着いて嬉しく思っています。これもひとえにブログ読んでいただいている皆様のおかげだと思っています。わけわからん文章やノートを見ていただき、心から感謝しております。
もっとも興味をそそられる力学系も、この章で学べるということなのでワクワクしています。夏休みから頑張ってきた甲斐があった。思えば何度もやめようかと思ったけど、何故か離れられんのよね。山本先生の記述って、難しいけどなんか美しさを感じてしまうんよね。
とりあえず、また挫けるかも分からんけど頑張けんね。
ところでタイトル、なんで「狭い」のか?
ラグランジュ方程式の解曲線は同一の点から何本でも引ける。解曲線が交差することもある。これは,同時刻における斜方投射で角度をいろいろ変えたものを想像すれば分かる。
しかし解曲線が交差しない1本に定まるメリットとはなんだらう?
4.1.1のように表現することで(q,ξ)の状態空間に引き上げて考える。
高校レベルの鉛直投射で考えてみようかな。発射時刻が同一なら初速度が異なっていても、解曲線は重なってしまう。もはや交差を超えて。

xとvに分けると多分グラフは交差しない。こういう意味なのだろうか。

4.1.1の二式のように捉えた(q,ξ)のTN空間上の経路は交差しないのだ、きっと。
「速度の場」なるものの「幾何学的身分」は、不透明である。以下がまだ良く分からんけど、確かにq,ξについて極めて非対称なのは一目瞭然ですね。
§4.1.2正準方程式
4.1.3の複雑な式を見通しよくする。最終的には4.1.15のように極めてすっきりさせる。
4.1.4で一般化運動量を定義するがこれは(q,q.,t)の函数である。
Lのルジャンドル変換を経てHはpを含む(q,p,t)の函数であることがわかる。(4.1.6の前の式)。従って運動量pを含む4.1.5はLではなくHで表す方が自然である。
L=φq.-Hを偏微分して4.1.8を得るが,最後の項の第1因子(ヘス行列)が0でないとすればラグランジアンは正則という意味になり,第2因子は0でなければならない。すなわち
dq/dt=∂H/∂p Ⅰ
まず一つ目の運動方程式が得られた。
また4.1.5より∂L/∂q=dp/dt,先の第2因子=を4.1.10に適用し
dp/dt=-∂H/∂q Ⅱ
で二つ目の運動方程式を得る。
改めてハミルトニアンはq,p,tの関数で
H(q,p,t)=pψ(q,p,t)-L(q,ψ(q,p,t),t)
と定義する。
ところでq.=ψ(q,p,t)やp=φ(q,q.,t)とわざわざ文字を変えるのは,q.やpが独立に動き回る独立変数であることを強調するためと思われる。
正準方程式
dq/dt=∂H/∂p
dp/dt=-∂H/∂q
のq,pは独立に動き回る正準変数という。互いに独立で対等な変数である。
pはもはやq,q.,tに従属せず,独立に動き回る「身分の変換」が行われた。
§4.1.3相空間と正準1形式
系の状態(力学)は形式ごとに以下の点で示される。
ラグランジュ形式 配位空間Nの 接バンドルT N(状態空間)上の点
ハミルトン形式 配位空間Nの余接バンドルT*N( 相空間)上の点
T*N上の点Qにおける運動量ベクトルdqが基底だから,
(θ)Q=pi(dqi)Q
となる。またQをくまなく動かして1形式
θ=pi(dqi)を得る。これを正準1形式という。
§4.1.4リーマン計量
L=T-Vのとき配位空間にはリーマン計量mij dqi dqjが備わる。
一般化運動量成分はpi=∂T/∂q.i=(m)ik (q.)gkと表される。
写真1
接空間に計量テンソルmを導入すると,以下のようにベクトルuとvの内積が定義できる。
計量テンソルmによって,速度ベクトル(v)Q=(q.)i(∂i)Qを写像すると,運動量ベクトル[(pi)(dqi)]Q=θQとなりQにおける運動量ベクトルを得る。
速度ベクトル→→→m→→→運動量ベクトル
Qをくまなく動かすと,計量テンソル場mを得る。
先の速度ベクトル場はmにより正準1形式となる。
速度ベクトル場→→→m→→→正準1形式
m場を介して,ベクトル場と1形式が1対1対応する。
§4.1.5拡大相空間
(q0,q1,q1,…qn,p1,p2,…,pn)の(2n+1)個の独立な変数の空間を拡大相空間と呼ぶ。正準1形式は Θ=θ-H(qpt)dt となる。
§4.2 Hベクトル場
§4.2.1 symplectic多様体
正準1形式はθ=pdqだから
正準2形式はdθ=dp∧dq:=Ωとなる。
正準2形式には、偶数2n次元の一般の多様体をq,pの局所座標をもつ多様体に変える役割がある。実際、4次元の多様体(z1,z2,z3,z4)に対して、4.2.3aに注意して4.2.2の後半を施すと、

これを頑張って計算すると、

dz1∧dz1などはどうせ0だが、気にせず計算を進めると

というようにz1,z2にqをz3,z4にpを割り振ったことになる。
繰り返しになるが、偶数次元の多様体MにΩ(すなわち4.2.2)が備わっていればq、pを局所座標系とする相空間を定義することができるのだ。このΩをシンプレクティック形式という。2形式の1つすなわち、2階の交代テンソル(交代行列)で表すことができるから、「形式」の部分を「交代テンソル場」と読みかえることもできると思う。つまり「シンプレクティック・テンソル場を備えた多様体は相空間である」と言えるのではないか?
p219「閉形式の非退化な2階交代テンソル場」というのが一般的な定義なのであろう。ちょっと難しく感じるので、ざっと捉えておく。4.2.5が一般の座標系にたいするシンプレクティック形式の定義で、「非退化⇔ωは正則」くらいに捉えておく。
全ての2n次元シンプレクティック多様体は4.2.2の局所座標系をもつすなわち相空間ですよというのは、上の計算みたいに簡単でなくダルブーの定理から言える。ダルブーの定理は、「任意の正則な交代行列は、シンプレクティック行列にできるとよ」という定理である(4.2.6)。
つぎのようにまとめられている。
物理学:相空間は正準2形式を備え、正準変数で表される。
数学 :シンプレクティック多様体はシンプレクティック形式を備え、標準座標で表される。zをシンプレクティック変数という。
4.2.5の次行「それゆえ‥」の式の展開は

§4.2.2座標系によらない表現
次がやりたいのでちょいと飛ばす。
4.2.8aを観察し、ベクトル場z.と1形式dHをつなぐのがシンプレクティック形式(2階共変テンソル場)である。
局所座標系によらない正準方程式は
<Ω|c. , ⚫︎>=-dH
となる。
ベクトル場と1形式を結びつけるといえば、§1.6.3で教えていただいたリーマン多様体である。リーマン多様体では計量テンソル場を介して反変ベクトル場と1形式が対応するのだった。テンソル場の種類(性質)によって多様体の性質が変わってくるのだ。リーマン多様体には距離(計量)が備わる。距離が備わっていないなら、例えば連続性だけ備えたものは位相空間といって位相幾何学の対象となる。
多様体の性質を裏付ける条件がだんだん理解できて嬉しい。酒に溺れず頑張った甲斐があった。
§4.2.3 Hベクトル場
ハミルトニアンベクトル場は、ハミルトニアンが生成するベクトル場である。
ハミルトニアンを与えると、フローの速度が指定される(4.2.20)。
ハミルトニアンベクトル場は4.2.19によって指定される。

4.2.11の左辺をc.だけにする。
シンプレクティック多様体では、正準2形式を介して、1形式とベクトル場が1対1に対応づけられる。ので、「相互に置き換わり得る」
Ωで写像しdHとなるベクトル場がvHである。

繰り返しになるが、
相空間にハミルトニアンHが与えられるとき、各点でのフローの速度は、ハミルトニアンによって生成される速度場vHによって指定される。これがハミルトニアンベクトル場である。
§4.3 力学系
§4.3.1 力学系とは
・正準2形式が備わっているとは限らない広義の相空間をNとする。
・広義の相空間の局所座標系をx=(x1,x2,…,xn)とする。
・相空間上にはベクトル場v(x,t)=(v1,v2,…)が与えられる。
・vi=vi(x1,x2,…,t)だから,ベクトル場の成分は相空間上の点Qごとに異なる。
・微分方程式たち
dx1/dt=v1(x1,x2,…,xn,t)
dx2/dt=v2(x1,x2,…,xn,t) …
dxn/dt=vn(x1,x2,…,xn,t)
・と相空間N(局所座標系x=(x1,x2,…,xn))とのセットを力学系という。
・力学系の例
2階微分があるのに調和振動が力学系とできるのは何故だろうか?
§4.3.2 相流と不変集合
ベクトル場の不動点
平衡解
周期解
安定
漸近安定
力学系4.3.11の例は分かりやすい。要
不安定な平衡解
漸近安定な周期解 リミットサイクル
・次の写像(変換?)全体を相流という。
φt:N→N:x(0)↦x(t)ただしx(t)はx(0)を通る。
相空間上の各点を初期値としてその点を分子とみなして、動点全体の集合を流体のようにみなす、という表現が大変分かりやすい。先生のこういった表現が大好きだ。
tを陽に含まない自律系は定常流となる。
相流は4.3.6の
恒等写像、積、逆写像
があるので群をなす。これを1径数変換群、one parameter変換群という。
積分曲線は第1積分たちの定める部分空間に限定され、これを不変集合という。
§4.3.3 平衡解 周期解 安定性
専門用語いろいろ。何回も読む。
力学系4.3.11の例が分かりやすし
§4.3.4 線形化方程式
力学系をなす微分方程式系は通常解析的には解けない。
代わりに平衡解や周期解の近くの安定や不安定を調べる。
不動点のまわりの線形化方程式をx.=Kxとし、Kを力学行列という。
これは必ずx=exp(tK)x0 と解ける。
ここで力学行列Kの性質をみることが肝要で、すなわち対角化可能かどうかだ。対角化できれば、固有値を用いて解を明示的に4.3.22のように表せる。
行列の指数関数については、岩波キーポイント行列と変換群が分かりやすいです。
§4.3.5 2次元での考察
条件付きで対角化可能な場合
2次元の場合
本文の通りに進めれば理解できる。





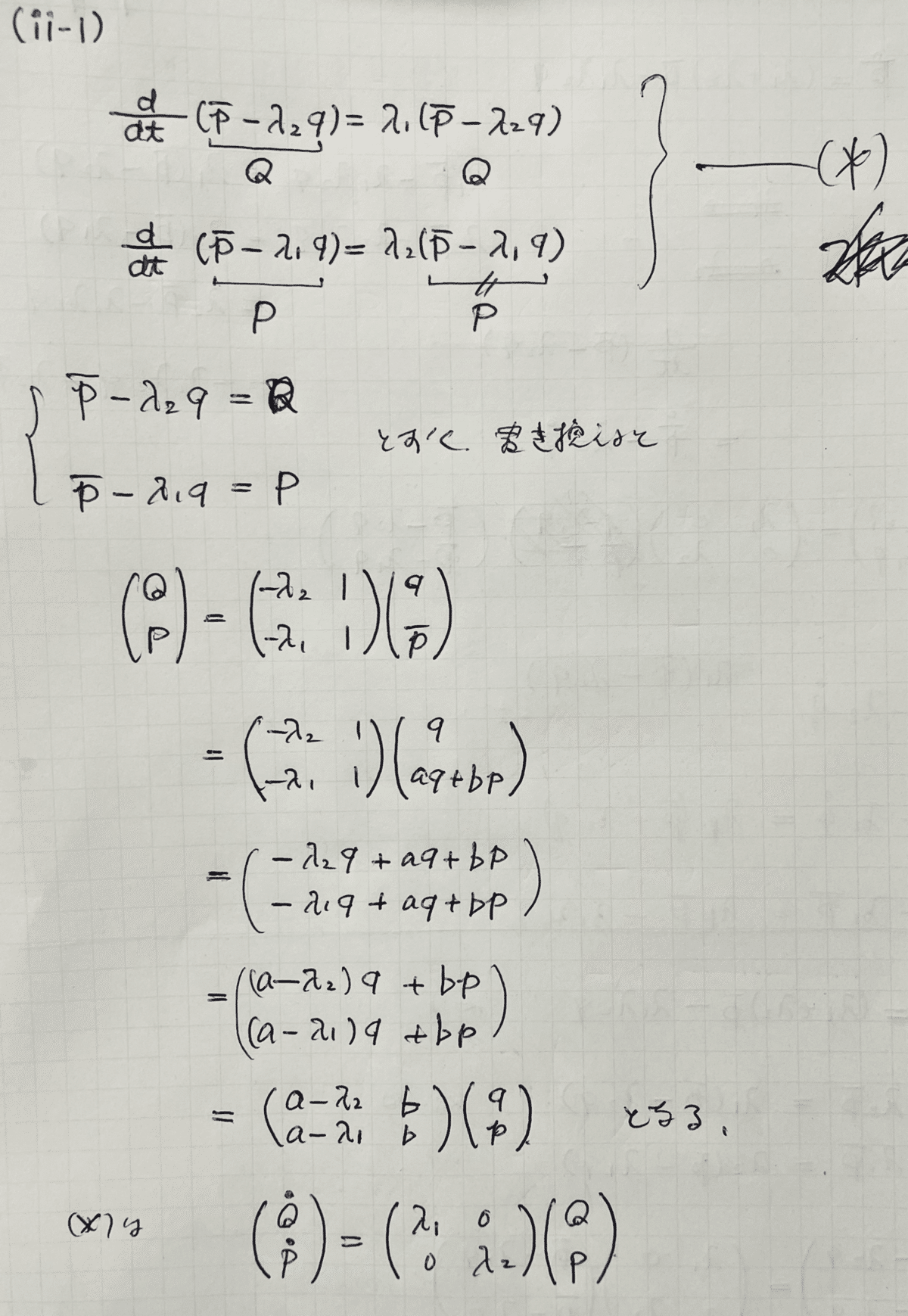

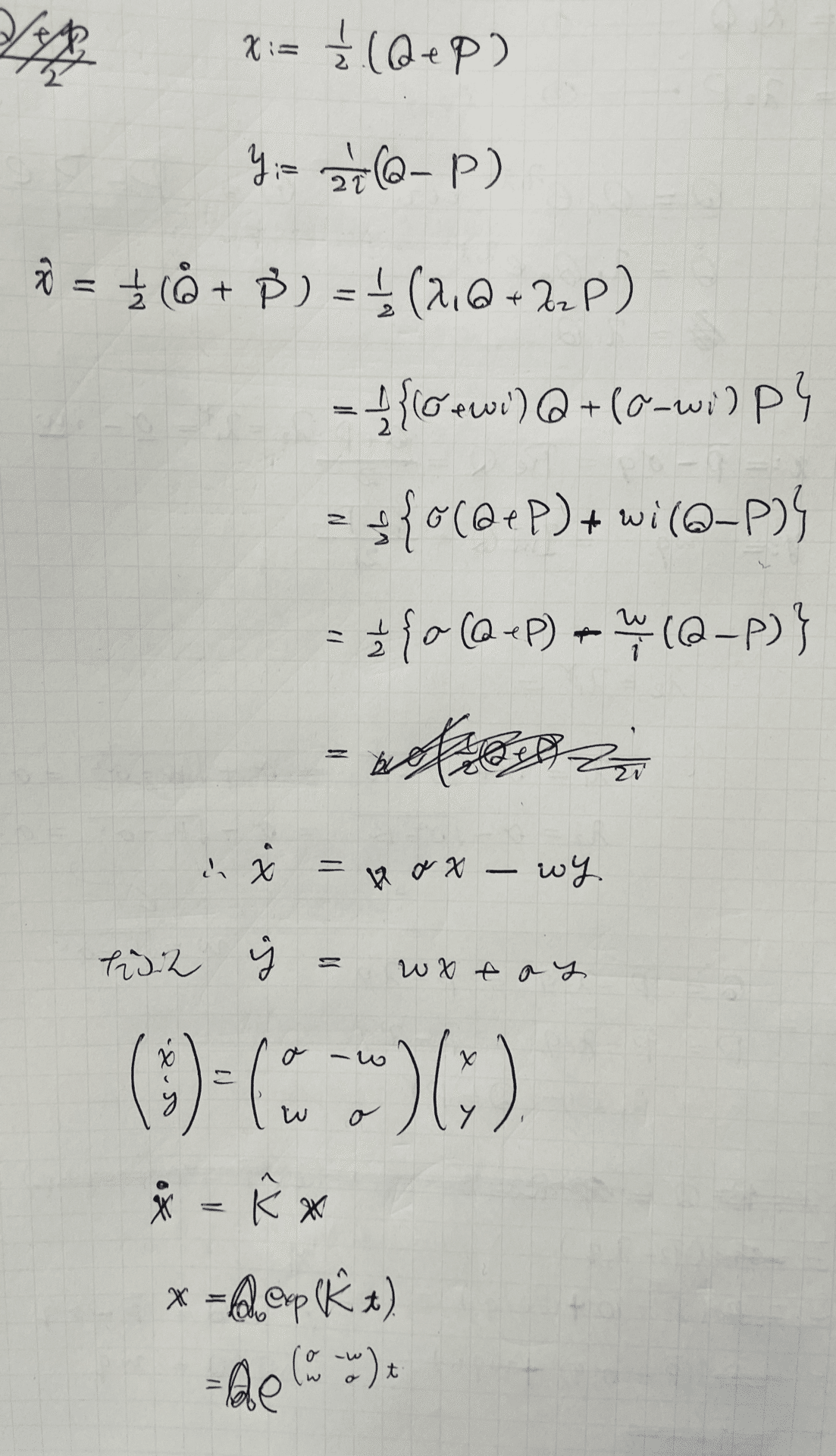

しかし4.3.32は次のようにも解ける。

行列の指数関数については岩波キーポイント行列と変換群を参照した。
力学行列が対角化できずとも、固有値がm重縮退なら、力学行列Kのmmの部分行列はジョルダンブロックまで変換可能である。
