
統計学が最強の学問である 実践編③:本書の分析手法(9種)の一覧表
読書ノート(143日目)
年末年始の読書テーマである
「統計学が最強~」の2冊目として、
本日もこちらの本からです。
・第3章:洞察の王道となる手法群
重回帰分析とロジスティック回帰
・統計学の王道「回帰分析」
・説明変数が量的な数値で表される場合は回帰分析を使う
・関連性の見落とし、見誤りはどのように生じるのか?
・例えば、営業スタッフの訪問回数と獲得契約数で散布図をつくり
回帰式を求めた際に、訪問回数と獲得契約数は横ばい(y=0x+3)と
なった際、訪問回数と獲得契約数は「一見何の関係も無さそう」となる
・ただし、ここにサブグループ情報として
「性別」のデータを追加し男性と女性で分けて分析すると
訪問回数と獲得契約数に正の相関が見られる。
ということも考え、見落としがあったこととなる。
・しかし、サブグループ解析はすぐに限界が来る
・サブグループ解析の場合、仮に性別と都道府県で分ける場合、
94のサブグループが作られ、分析に使える元データが1000件あった
としても、サブグループでは平均で約10件ずつになってしまう
※分析に用いるデータが少ないと誤差が大きくなる
・くわえて、94回も単回帰分析を実施し大量の結果に
目を通すことも面倒である
・このようなサブグループの限界を回避しつつ、
他の要因が結果をゆがめるリスクを避ける方法が「重回帰分析」
・重回帰分析により、複数の説明変数とアウトカムとの関係性を
「一気に分析する」ことができる
・量的な数値でない説明変数(性別など)についても分析可能で、
その場合はダミー変数化(例:女性を0、男性を1)し分析する
・交互作用項
例えばマーケティング戦略を検討する際に、
DMの送付が男性にのみ効いており、女性にはあまり効いていない
ということが散布図から分かっている場合
・重回帰分析では、交互作用項を用いて分析すると良い
(「性別×DM送付数」を変数とする)
女性(0)×DM送付数
男性(1)×DM送付数
・そうすることで
「男性のみに送ったDM送付数」「女性のみに送ったDM送付数」
の効果と95%信頼区間を解析することができる
・このように変化をつけにくい説明変数×変化をつけやすい説明変数という
交互作用を検討することで、「誰にこの施策を打つべきか」を
明らかにすることができる
・アウトカムが連続値ではなく、陽性・陰性などの0か1の2値で
表される場合は、「ロジスティック回帰」を用いる
・アウトカムが3つ以上のカテゴリーに分かれる場合
・例えば、顧客満足度アンケートで大変不満(0点)~大変満足(3点)まで
4段階の選択肢がある場合、量的な数値型データとして扱う際は、
大変不満(0点)から大変満足(3点)まで等間隔に並んでいる必要がある
・ただし、実際の感情としては、大変不満や大変満足だけが
他の選択肢と大きく離れていることも考えられ、
すべて同じ1点分の差と考えることに解析結果を共有する相手が
納得するかどうかは解析の前に検討が必要
・この問題を2値のアウトカムを分析するロジスティック回帰で
扱う場合は、「この満足度の項目から何を知りたいのか」と考えて
二値変換化することが大切
・例えば、この満足度調査から「大変不満」という顧客を減らし
離反防止をしたいのなら、「大変不満」と、「それ以外」で二値変換する
また仮に、ポジティブな口コミ数の向上を目指し「大変満足」という
顧客を増やしたいなら、「大変満足」と、「それ以外」で二値変換する
・両方が重要なのであれば両方の分析を行い、回帰係数(オッズ比)のうち
どこが共通していてどこが異なるか、というところを考察する
(補足)
・二値変換せずに、大変不満(0点)~大変満足(3点)の3つ以上の
カテゴリーデータのまま分析する「順序ロジスティック回帰」
という手法もあるにはあるが、大変不満とやや不満の違いも、
やや満足と大変満足の違いも、同じ説明変数で同じように関連している
という仮定をおくことになる
・現実的には、不満を感じる理由だけをいくら減らしても
「大変満足」に繋がるとは限らないため、いきなりこの手法を
使うというのはあまりおすすめではない
・また、順序性がない3カテゴリー以上の質的変数に対しても、
そのまま分析できる「多値ロジスティック回帰」と呼ばれる手法が
存在しているが、因果関係の洞察を重視する、という本書の
立場に基づくと、横着せずにアウトカムを二値変数化して
通常のロジスティック回帰を行った方が結果の解釈がしやすい
今回は統計学の王道である
「回帰分析」についてでした。
また、この章では筆者が
データ分析の手法を整理して一覧表
で示してくださっています。
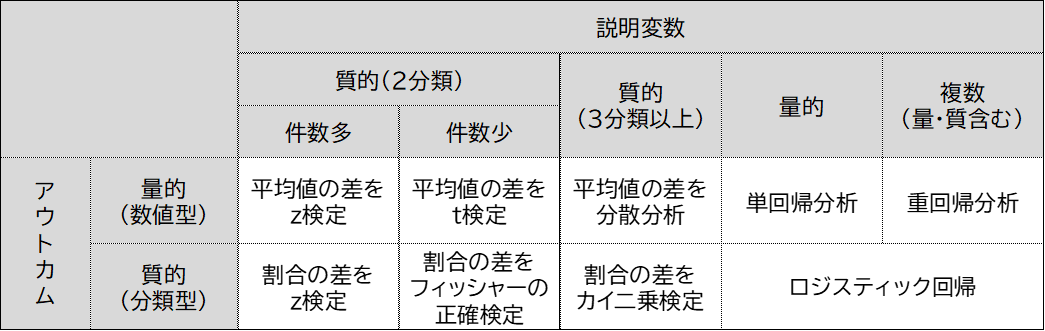
説明変数とアウトカムのデータ型に応じて
9つの手法を使い分けることになるのですが、
本書の中で紹介されていた
「データ量が多い時でもt検定で良い」
ということを反映すると、
以下のように再整理ができそうです。

さらに単回帰分析と重回帰分析を強いてまとめれば7種になりますが、
それは本意ではないかなと思い、8種に留めることにしました
さて、本書の中でも紹介されていた
重回帰分析での交互作用項を使った
分析は非常に興味深く、
もしこれを見つけることができれば、
分析依頼者側のサプライズにもなり
分析レポートの質を一気に上げられそう!
なのですが、
そもそも肝心なのは、どうやって見つけるか…
これは個人的な考えですが、
分析依頼者の仮説から当たりをつけるか、
性別・年代などの分類ごとに
総当たりで散布図を並べてみて、
明らかに傾きが異なっている変数を
見つけ出す、というのが現実的でしょうか。
また、重回帰分析は万能で強力は反面、
注意事項や取説もあり…
・説明変数を増やすほど、学習データへの
当てはまりの良さが上がる
オーバーフィッテイングが発生してしまう
・各説明変数は相互に影響し合わない
「独立」している必要がある
これら2つが主な注意事項でしょうか。
・オーバーフィッティングを避けるための手法たち
最終的な回帰式に用いる説明変数を調整する方法
・フォワード法
まず全ての説明変数で単回帰分析を実施、
p値が小さいものから順に説明変数を追加する
・バックワード法
全ての説明変数を含んだ重回帰分析を実施し、
p値が大きいものから順に説明変数を除外
・ステップワイズ法(両者の良いところどりでオススメ)
まずフォワード法と同様にp値の小さい説明変数を追加し始め、
少し緩めのp値(通常0.1以上)を示した説明変数が生じたら削除し、
追加も削除もできなくなったら終了する
・AIC
説明変数の数の割に当てはまりがよいかどうかを示す指標
・クロスバリデーション法:
回帰式を求める分析用データと検証用データを分けて評価する方法
…と、奥が深い重回帰分析ですが
筆者が「統計学の王道」と言うほどに、
使いこなせれば大きな武器になります!
ところで、私が2023年に分析して
お客様に納品した分析レポートも
既にすべて検収済ではあるものの、
相手側へのサプライズが少なかったのでは?
と思い返す分析が少なくとも2つあり…
どうすればもっと良い分析ができただろう?
改めてデータを見つめ直してみたら何か
新しい発見があるのではないか?
という思いを、本書を読みながら
ふつふつと感じていました。
幸いなことに、24年2月に同じお客様に
関連した分析レポートを納品させていただく
機会があるので、1月中は過去の分析を見直し
ひそかに再挑戦するチャンスだとも考えています。
自分の信用残高を少しずつでも高め続けられるよう
今年は一層、真摯に仕事に取組もう!という
想いを固め、今日はこの辺で締めたいと思います。
途中からまとまりの無い話に
なってしまいましたが…
最後まで読んでくださり
どうもありがとうございました!!
それではまたー!😉✨
