
中学でも分かる➂「平方根」
平方とは
同じ数を2回掛けることを平方または2乗(square)といいます。
平方は、右肩に $${2}$$ をつけて次のように表します。
$${2}$$ の平方は $${2\times2=2^2=4}$$
$${3}$$ の平方は $${3\times3=3^2=9}$$
$${4}$$ の平方は $${4\times4=4^2=16}$$
一方、平方根(square root)とは、$${2}$$ 回かけてある数になるとき、そのかける前の数です。例えば「$${4}$$ の平方根を求めなさい」とは
「どんな数を $${2}$$ 回かけたら $${4}$$ になりますか?」
と聞いています。$${2}$$ 回かけて $${4}$$ になるそのルーツ (root) を聞いてます。
$${2}$$ 回かけて $${4}$$ になる数は
$${2\times2=2^2=4}$$
$${(-2)\times(-2)={(-2)}^2=4}$$
と、$${2}$$ と $${-2}$$ の2つあるので
$${4}$$ の平方根は $${2}$$ と $${-2}$$
になります。
下図のように、平方根と2乗は互いに逆の演算となります。
$$
\begin{align*}
\\[-14pt]
&\hspace{7pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&4\hspace{39pt}2, -2\\[-12.5pt]
&\hspace{7pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
以下、この平方根について詳しく解説し、さらに立方根(3乗恨)、累乗根($${n}$$ 乗根)へと話を進めていきます。なお、平方根は中学3年で、立方根、累乗根は高校2年で習います。
平方根とは
まずは、平方根について具体例を上げながら解説します。
$${4}$$ の平方根とは「$${2}$$ 乗して $${4}$$ になる数」のことです。$${2}$$ 乗して $${4}$$ になる数は、$${2}$$ と $${-2}$$ の2つあります。
$${2^2=4}$$ $${(-2)^2=4}$$
よって、$${4}$$ の平方根は $${2}$$ と $${-2}$$ になり、2つ合わせて $${\pm2}$$ と表します。
$$
\begin{align*}
\\[-14pt]
&\hspace{7pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&4\hspace{39pt}2, -2\\[-12.5pt]
&\hspace{7pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
$${9}$$ の平方根とは「$${2}$$ 乗して $${9}$$ になる数」のことです。$${2}$$ 乗して $${9}$$ になる数は、$${3}$$ と $${-3}$$ の2つあります。
$${3^2=9}$$ $${(-3)^2=9}$$
よって、$${9}$$ の平方根は $${3}$$ と $${-3}$$ になり、2つ合わせて $${\pm3}$$ と表します。
$$
\begin{align*}
\\[-14pt]
&\hspace{7pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&9\hspace{39pt}3, -3\\[-12.5pt]
&\hspace{7pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
$${2}$$ の平方根とは「$${2}$$ 乗して $${2}$$ になる数」のことです。$${2}$$ 乗して $${2}$$ になる数は整数の範囲 $${(\cdots, -2, -1, 0, 1, 2, \cdots)}$$ には存在しないので、ルート $${\sqrt{\hspace{10pt}}}$$ という記号を用いて $${\sqrt{2}}$$ と $${-\sqrt{2}}$$ で表します。つまり
$${{\big(\sqrt{2}\,\big)}^2=2}$$ $${{\big(-\sqrt{2}\,\big)}^2=2}$$
よって、$${2}$$ の平方根は $${\sqrt{2}}$$ と $${-\sqrt{2}}$$ になり、2つ合わせて $${\pm\sqrt{2}}$$ と表します。
$${\sqrt{2}}$$ は無理数になります。
$${\sqrt{2}=1.41421356 \cdots}$$ $${\scriptsize{(ひとよひとよにひとみごろ)}}$$
無理数とは、繰り返しのない無限に続く小数です(参考1で数の分類)(参考2で無理数の発見)。
$$
\begin{align*}
\\[-14pt]
&\hspace{7.5pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&2\hspace{39pt}\sqrt{2}, -\sqrt{2}\\[-12.5pt]
&\hspace{7.5pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
$${3}$$ の平方根とは「$${2}$$ 乗して $${3}$$ になる数」のことです。$${2}$$ 乗して $${3}$$ になる数は整数の範囲には存在しないので、ルート $${\sqrt{\hspace{10pt}}}$$ という記号を用いて $${\sqrt{3}}$$ と $${-\sqrt{3}}$$ で表します。つまり
$${{\big(\sqrt{3}\,\big)}^2=3}$$ $${{\big(-\sqrt{3}\,\big)}^2=3}$$
よって、$${3}$$ の平方根は $${\sqrt{3}}$$ と $${-\sqrt{3}}$$ になり、2つ合わせて $${\pm\sqrt{3}}$$ と表します。
$${\sqrt{3}}$$ は無理数になります。
$${\sqrt{3}=1.7320508\cdots}$$ $${\scriptsize{(ひとなみにおごれや)}}$$
$$
\begin{align*}
\\[-14pt]
&\hspace{7.5pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&3\hspace{39pt}\sqrt{3}, -\sqrt{3}\\[-12.5pt]
&\hspace{7.5pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
$${5}$$ の平方根とは「$${2}$$ 乗して $${5}$$ になる数」のことです。$${2}$$ 乗して $${5}$$ になる数は整数の範囲には存在しないので、ルート $${\sqrt{\hspace{10pt}}}$$ という記号を用いて $${\sqrt{5}}$$ と $${-\sqrt{5}}$$ で表します。つまり
$${{\big(\sqrt{5}\,\big)}^2=5}$$ $${{\big(-\sqrt{5}\,\big)}^2=5}$$
よって、$${5}$$ の平方根は $${\sqrt{5}}$$ と $${-\sqrt{5}}$$ になり、2つ合わせて $${\pm\sqrt{5}}$$ と表します。
$${\sqrt{5}}$$ は無理数になります。
$${\sqrt{5}=2.2360679\cdots}$$ $${\scriptsize{(ふじさんろくおうむなく)}}$$
$$
\begin{align*}
\\[-14pt]
&\hspace{7.5pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&5\hspace{39pt}\sqrt{5}, -\sqrt{5}\\[-12.5pt]
&\hspace{7.5pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
以上を踏まえ、あらためて平方根を定義します。
<平方根の定義>
$${a}$$ を正の実数 とする $${(a >0)}$$。
このとき、$${2}$$ 乗すると $${a}$$ になる数を $${a}$$ の平方根、または2乗恨(square root)という。$${a}$$ の平方根のうち
正の方を $${\sqrt{a}}$$
負の方を $${-\sqrt{a}}$$
と表す。
$$
\begin{align*}
\\[-14pt]
&\hspace{7.5pt}\xrightarrow[]{\hspace{0pt}平方根\hspace{2pt}}\\[-12.5pt]
&a\hspace{39pt}\sqrt{a}, -\sqrt{a}\\[-12.5pt]
&\hspace{7.5pt}\xleftarrow[\hspace{5pt}2 乗\hspace{5pt}]{}
\end{align*}
$$
***
例えば
$${1}$$ の平方根は $${\sqrt{1}=1}$$ と $${-\sqrt{1}=-1}$$
$${2}$$ の平方根は $${\sqrt{2}}$$ と $${-\sqrt{2}}$$
$${3}$$ の平方根は $${\sqrt{3}}$$ と $${-\sqrt{3}}$$
$${4}$$ の平方根は $${\sqrt{4}=2}$$ と $${-\sqrt{4}=-2}$$
$${5}$$ の平方根は $${\sqrt{5}}$$ と $${-\sqrt{5}}$$
$${9}$$ の平方根は $${\sqrt{9}=3}$$ と $${-\sqrt{9}=-3}$$
以上のように、平方根にはプラスとマイナスの2つがあります。このことを、グラフを用いて解説します。
平方根についてグラフで解説
正の実数 $${a (>0)}$$ の平方根は、方程式
$${x^2=a}$$
の解になります。例えば
$${1}$$ の平方根は $${x^2=1}$$ の解で $${1}$$ と $${-1}$$
$${2}$$ の平方根は $${x^2=2}$$ の解で $${\sqrt{2}}$$ と $${-\sqrt{2}}$$
$${3}$$ の平方根は $${x^2=3}$$ の解で $${\sqrt{3}}$$ と $${-\sqrt{3}}$$
$${4}$$ の平方根は $${x^2=4}$$ の解で $${2}$$ と $${-2}$$
$${5}$$ の平方根は $${x^2=5}$$ の解で $${\sqrt{5}}$$ と $${-\sqrt{5}}$$
$${9}$$ の平方根は $${x^2=9}$$ の解で $${3}$$ と $${-3}$$
$${\hspace{23pt}\vdots}$$
一般に、
正の実数 $${a (>0)}$$ の平方根は $${x^2=a}$$ の解で $${\sqrt{a}}$$ と $${-\sqrt{a}}$$
となります。
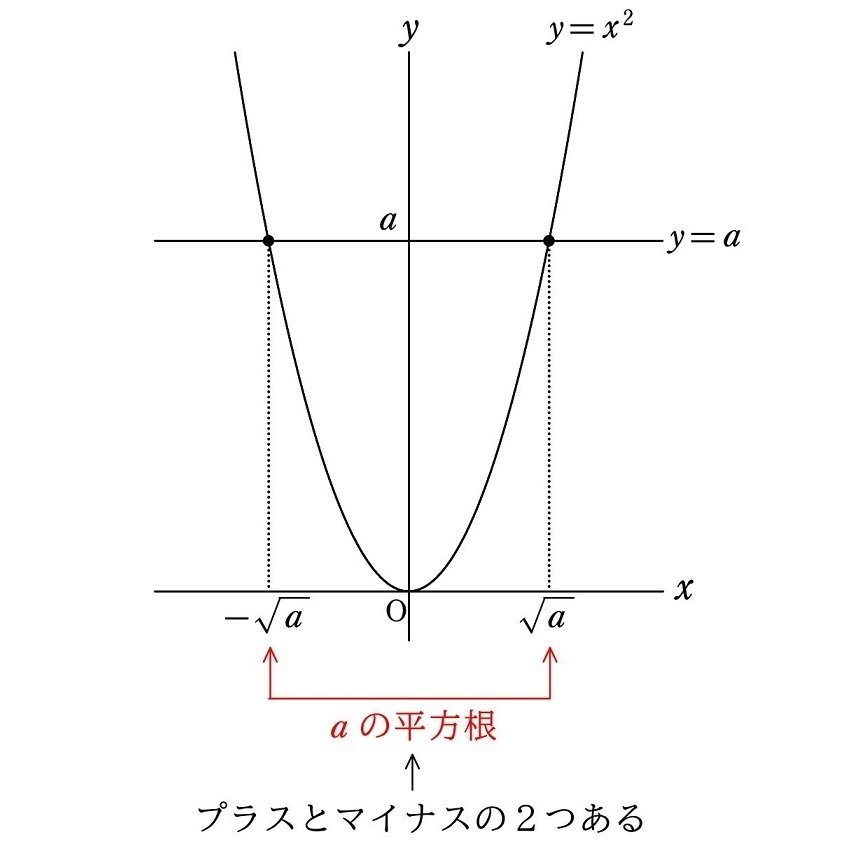
さらに、$${x^2=a}$$ の解は、曲線 $${y=x^2}$$ と直線 $${y=a}$$ の共有点(交点や接点)の $${x}$$ 座標になります。

よって、$${a (>0)}$$ の平方根が
$${\sqrt{a}}$$ と $${-\sqrt{a}}$$
の2つであることは、下図のように視覚的に分かります。
なお、曲線 $${y=x^2}$$ は、原点を頂点とする下に凸の放物線です。直線 $${y=a}$$ は、$${x}$$ 軸に平行な直線です。$${x}$$ がどのような値でも、つねに $${y=a}$$ となる直線です。どちらも中学3年で習います。
一般に、正の実数の平方根は、プラスとマイナスの2つがあります。
例えば $${1}$$ の平方根は、曲線 $${y=x^2}$$ と直線 $${y=1}$$ の共有点の $${x}$$ 座標なので、$${1}$$ と $${-1}$$ の2つあります。

$${4}$$ の平方根は、曲線 $${y=x^2}$$ と直線 $${y=4}$$ の共有点の $${x}$$ 座標なので、$${2}$$ と $${-2}$$ の2つあります。
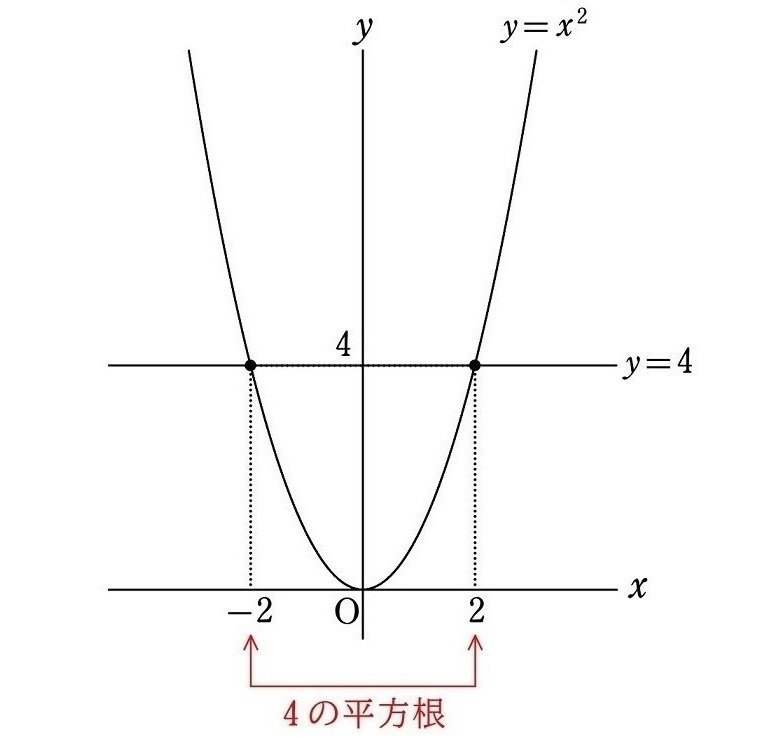
$${9}$$ の平方根は、曲線 $${y=x^2}$$ と直線 $${y=9}$$ の共有点の $${x}$$ 座標なので、$${3}$$ と $${-3}$$ の2つあります。

$${2}$$ の平方根は、曲線 $${y=x^2}$$ と直線 $${y=2}$$ の共有点の $${x}$$ 座標なので、$${\sqrt{2}}$$ と $${-\sqrt{2}}$$ の2つあります。

$${3}$$ の平方根は、曲線 $${y=x^2}$$ と直線 $${y=3}$$ の共有点の $${x}$$ 座標なので、$${\sqrt{3}}$$ と $${-\sqrt{3}}$$ の2つあります。

$${0}$$ の平方根は、曲線 $${y=x^2}$$ と直線 $${y=0}$$($${x}$$ 軸)の共有点の $${x}$$ 座標なので、 $${0}$$ の1つのみです。両者は原点 O で接します。
なお、直線 $${y=0}$$ は $${x}$$ 軸そのものになります。$${x}$$ がどのような値でも、つねに $${y=0}$$ となる直線は $${x}$$ 軸そのものです。

(注)負の実数の平方根は実数の範囲では存在しないこと。
負の実数の平方根、例えば $${-4}$$ の平方根は、実数の範囲では存在しません(つまり、$${2}$$ 乗して負になる実数は存在しない)。このことは、曲線 $${y=x^2}$$ と直線 $${y=-4}$$ には共有点が存在しないことからも分かります。

複素数の範囲まで数を広げれば $${-4}$$ の平方根は存在しますが、複雑にならないよう、本記事では実数の範囲で考えます。複素数の解説は別の機会にします。簡単には(参考3)をご覧ください。
次に立方恨(3乗根)について、例を上げながら解説します。
立方根とは
$${1}$$ の立方根とは「$${3}$$ 乗して $${1}$$ になる数」のことです。$${3}$$ 乗して $${1}$$ になる数のうち、実数であるものは $${1}$$ の1つのみです。
$${1^3=1}$$
よって、$${1}$$ の立方根のうち、実数であるものは $${1}$$ になります。
(注)1 の立方恨には複素数もある。
複素数の範囲で考えると、$${1}$$ の立方根は、実数である $${1}$$ 以外にも2つの虚数があります。一般に、実数の3乗根は3つあり、1つは実数、他の2つは虚数になりますが、このことについては(参考4)で簡単に解説します。本記事では実数の立方根のみを考えます。
$${8}$$ の立方根とは「$${3}$$ 乗して $${8}$$ になる数」のことです。$${3}$$ 乗して $${8}$$ になる数のうち、実数であるものは $${2}$$ の1つのみです。
$${2^3=8}$$
よって、$${8}$$ の立方根のうち、実数であるものは $${2}$$ になります。
$${27}$$ の立方根とは「$${3}$$ 乗して $${27}$$ になる数」のことです。$${3}$$ 乗して $${27}$$ になる数のうち、実数であるものは $${3}$$ の1つのみです。
$${3^3=27}$$
よって、$${27}$$ の立方根のうち、実数であるものは $${3}$$ になります。
$${-1}$$ の立方根とは「$${3}$$ 乗して $${-1}$$ になる数」のことです。$${3}$$ 乗して $${-1}$$ になる数のうち、実数であるものは $${-1}$$ の1つのみです。
$${{(-1)}^3=-1}$$
よって、$${-1}$$ の立方根のうち、実数であるものは $${-1}$$ になります。
(注)負の実数の立方根
負の実数の平方根(2乗恨)は実数の範囲では存在しませんが、負の実数の立方根(3乗根)は、実数の範囲でただ1つ存在することに注意しましょう。
(例)$${-1}$$ の平方根は実数の範囲では存在しない。
$${{〇}^2=-1}$$ となる $${〇}$$ は実数の範囲では存在しない。
$${-1}$$ の立方恨のうち、実数であるものは $${-1}$$ の1つのみ。
$${{(-1)}^3=-1}$$
$${-8}$$ の立方根とは「$${3}$$ 乗して $${-8}$$ になる数」のことです。$${3}$$ 乗して $${-8}$$ になる数のうち、実数であるものは $${-2}$$ の1つのみです。
$${{(-2)}^3=8}$$
よって、$${-8}$$ の立方根のうち、実数であるものは $${-2}$$ になります。
$${-27}$$ の立方根とは「$${3}$$ 乗して $${-27}$$ になる数」のことです。$${3}$$ 乗して $${-27}$$ になる数のうち、実数であるものは $${-3}$$ の1つのみです。
$${{(-3)}^3=-27}$$
よって、$${-27}$$ の立方根のうち、実数であるものは $${-3}$$ になります。
$${2}$$ の立方根とは「$${3}$$ 乗して $${2}$$ になる数」のことです。$${3}$$ 乗して $${2}$$ になる数は整数の範囲には存在しないので、$${\sqrt[3]{\hspace{8pt}}}$$ という記号を用いて $${\sqrt[3]{2}}$$ と表します。つまり
$${{\big(\sqrt[3]{2}\,\big)}^3=2}$$
よって、$${2}$$ の立方根のうち、実数であるものは $${\sqrt[3]{2}}$$ になります。
$${5}$$ の立方根とは「$${3}$$ 乗して $${5}$$ になる数」のことです。$${3}$$ 乗して $${5}$$ になる数は整数の範囲には存在しないので、$${\sqrt[3]{\hspace{8pt}}}$$ という記号を用いて $${\sqrt[3]{5}}$$ と表します。つまり
$${{\big(\sqrt[3]{5}\,\big)}^3=5}$$
よって、$${5}$$ の立方根のうち、実数であるものは $${\sqrt[3]{5}}$$ になります。
$${-2}$$ の立方根とは「$${3}$$ 乗して $${-2}$$ になる数」のことです。$${3}$$ 乗して $${-2}$$ になる数は整数の範囲には存在しないので、$${\sqrt[3]{\hspace{8pt}}}$$ という記号を用いて $${\sqrt[3]{-2}}$$ と表します。つまり
$${{\big(\sqrt[3]{-2}\,\big)}^3=-2}$$
よって、$${2}$$ の立方根のうち、実数であるものは $${\sqrt[3]{-2}}$$ になります。
$${-5}$$ の立方根とは「$${3}$$ 乗して $${-5}$$ になる数」のことです。$${3}$$ 乗して $${-5}$$ になる数は整数の範囲には存在しないので、$${\sqrt[3]{\hspace{8pt}}}$$ という記号を用いて $${\sqrt[3]{-5}}$$ と表します。つまり
$${{\big(\sqrt[3]{-5}\,\big)}^3=-5}$$
よって、$${-5}$$ の立方根のうち、実数であるものは $${\sqrt[3]{-5}}$$ になります。
以上を踏まえ、改めて立方根を定義します。
<立方根の定義>
$${a}$$ の範囲はすべての実数とする。
$${3}$$ 乗すると $${a}$$ になる数を $${a}$$ の立方根、または3乗恨(cube root, cubic root)という。$${a}$$ の立方根のうち、実数であるものはただ一つ存在し、これを
$${\sqrt[3]{a}}$$
と表す。
***
例えば
$${1}$$ の立方根は $${\sqrt[3]{1}=1}$$
$${2}$$ の立方根は $${\sqrt[3]{2}}$$
$${3}$$ の立方根は $${\sqrt[3]{3}}$$
$${8}$$ の立方根は $${\sqrt[3]{8}=2}$$
$${27}$$ の立方根は $${\sqrt[3]{27}=3}$$
$${-1}$$ の立方根は $${\sqrt[3]{-1}=-1}$$
$${-2}$$ の立方根は $${\sqrt[3]{-2}}$$
$${-3}$$ の立方根は $${\sqrt[3]{-3}}$$
$${-8}$$ の立方根は $${\sqrt[3]{-8}=-2}$$
$${-27}$$ の立方根は $${\sqrt[3]{-27}=-3}$$
立方根についてグラフで解説
一般に、実数の立方根のうち、実数であるものはただ1つ存在します。
このことをグラフを用いて解説します。
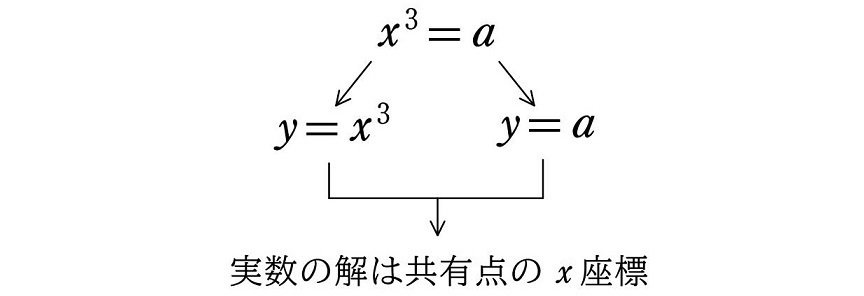
実数 $${a}$$ の立方根は、方程式
$${x^3=a}$$
の解になります。そのうち実数の解は、曲線 $${y=x^3}$$ と直線 $${y=a}$$ の共有点の $${x}$$ 座標になります。
ここで、$${y=x^3}$$ のグラフを書いてみましょう。
下のようないくつかの点を $${xy}$$ 座標に打ち込み、それらの点をなめらかに結ぶことによって、$${y=x^3}$$ のグラフの概形が描けます。
$${x=2}$$ のとき
$${y=2^3=8}$$ より P$${\hspace{-3pt}(2, 8)}$$
$${x=1}$$ のとき
$${y=1^3=1}$$ より Q$${\hspace{-3pt}(1, 1)}$$
$${x=0}$$ のとき
$${y=0^3=0}$$ より R$${\hspace{-3pt}(0, 0)}$$
$${x=-1}$$ のとき
$${y={(-1)}^3=-1}$$ より S$${\hspace{-3pt}(-1, -1)}$$
$${x=-2}$$ のとき
$${y={(-2)}^3=-8}$$ より T$${\hspace{-3pt}(-2, -8)}$$
よって、$${y=x^3}$$ のグラフは

実数 $${a}$$ の立方根は、方程式
$${x^3=a}$$
の解です。そのうち実数であるものは、曲線 $${y=x^3}$$ と直線 $${y=a}$$ の共有点の $${x}$$ 座標なので、 $${a}$$ の立方根が $${\sqrt[3]{a}}$$ のただ1つであることは、下図のように視覚的に分かります。

例えば、$${8}$$ の立方根のうち実数であるものは、曲線 $${y=x^3}$$ と直線 $${y=8}$$ の共有点の $${x}$$ 座標なので、$${2}$$ の1つのみになります。

$${-8}$$ の立方根のうち実数であるものは、曲線 $${y=x^3}$$ と直線 $${y=-8}$$ の共有点の $${x}$$ 座標なので、$${-2}$$ の1つのみになります。

$${5}$$ の立方根のうち実数であるものは、曲線 $${y=x^3}$$ と直線 $${y=5}$$ の共有点の $${x}$$ 座標なので、$${\sqrt[3]{5}}$$ の1つのみになります。
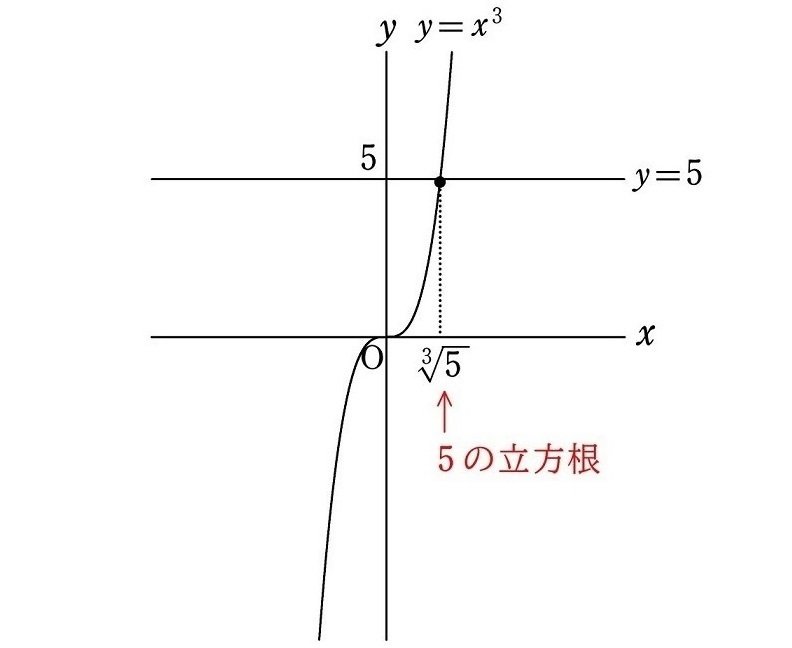
$${-5}$$ の立方根のうち実数であるものは、曲線 $${y=x^3}$$ と直線 $${y=-5}$$ の共有点の $${x}$$ 座標なので、$${\sqrt[3]{-5}}$$ の1つのみになります。
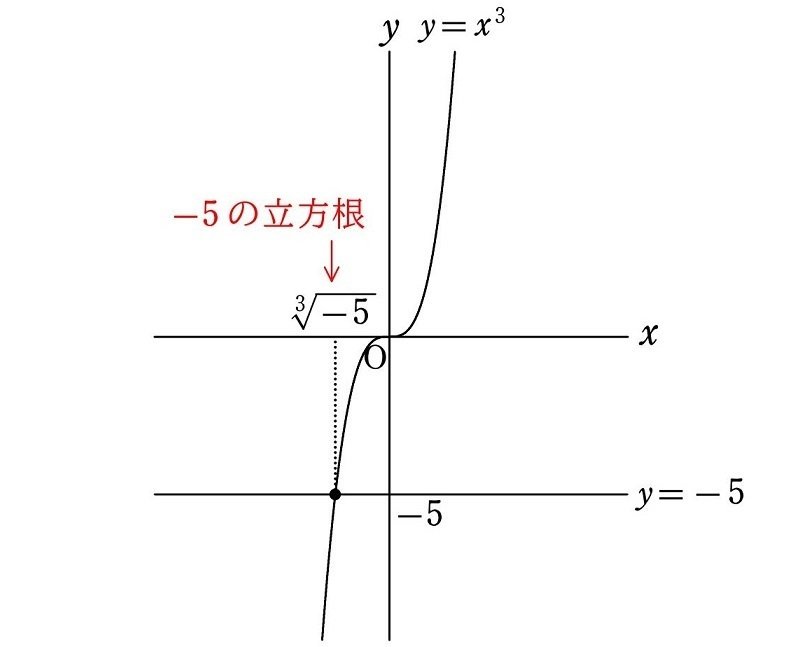
このように、実数となる立方根は1つだけ存在し、$${a}$$ が正の実数 $${(a>0)}$$ だとその立方恨も正であり、$${a}$$ が負の実数 $${(a<0)}$$ だとその立方恨も負になります。
$${a=2}$$ のとき $${\sqrt[3]{2}>0}$$
$${a=-2}$$ のとき $${\sqrt[3]{-2}<0}$$
n乗根について
最後にまとめとして、$${n}$$ 乗恨の定義を与えます。これまでの内容を一般的にまとめたものです。これまでの解説と合わせて読むことによって理解できるかと思います。
なお、考える数の範囲は実数で考えます。複素数まで拡張することは可能ですが、同時にやると内容が複雑になるので複素数の話は別の機会にします。
<n 乗恨の定義>
一般に、$${n}$$ を自然数 $${(1, 2, 3, \cdots)}$$ とするとき、$${n}$$ 乗すると $${a}$$ になる数を $${a}$$ の $${\bm{n}}$$ 乗恨(n-th root)という。つまり
$${2}$$ 乗すると $${a}$$ になる数を $${a}$$ の $${2}$$ 乗恨(平方根)
$${3}$$ 乗すると $${a}$$ になる数を $${a}$$ の $${3}$$ 乗恨(立方根)
$${4}$$ 乗すると $${a}$$ になる数を $${a}$$ の $${4}$$ 乗恨
$${\hspace{11.5pt}\vdots}$$
これら ○ 乗根を、まとめて累乗根(radical root)という。
$${a}$$ の $${n}$$ 乗恨は、$${n}$$ 次方程式
$$
\begin{align*}
x^n=a
\end{align*}
$$
の解になる。
ここで、$${n}$$ が偶数か奇数かで状況が違ってくるので
(case1) $${n}$$ が偶数のとき。
(case2) $${n}$$ が奇数のとき(ただし $${1}$$ を除く)。
で場合分けをする。
(case1) $${n}$$ が偶数のとき。
つまり2乗恨(平方根)、4乗恨、6乗恨、$${\cdots}$$ のとき。
正の実数 $${a (>0)}$$ の $${n}$$ 乗恨のうち、実数であるものは正と負の1つずつあり、正の方を $${\sqrt[n]{a}}$$、負の方を $${-\sqrt[n]{a}}$$ と表す。
なお、2乗恨(平方根)は
$${\sqrt[2]{2}=\sqrt{2}}$$
と、左肩の "2" を省略する。
(例)$${2}$$ の平方根は $${\sqrt{2}, -\sqrt{2}}$$
$${4}$$ の平方根は $${\sqrt{4}=2, -\sqrt{2}=-2}$$
$${2}$$ の4乗恨は $${\sqrt[4]{2}, -\sqrt[4]{2}}$$
$${16}$$ の4乗恨は $${\sqrt[4]{16}=2, -\sqrt[4]{16}=-2}$$
$${a (>0)}$$ の $${n}$$ 乗恨のうち実数であるものは、曲線 $${y=x^n}$$ と直線 $${y=a}$$ の共有点の $${x}$$ 座標として視覚化される。
一般に $${n}$$ が偶数のとき、$${y=x^n}$$ のグラフは、下図のように下に凸のU字カーブのグラフになる。それと直線 $${y=a}$$ との交点の $${x}$$ 座標が、$${a}$$ の $${n}$$ 乗恨 $${\sqrt[n]{a}, -\sqrt[n]{a}}$$ になる。

$${0}$$ の $${n}$$ 乗恨については $${\sqrt[n]{0}=0}$$ と定める。
なお、負の実数 $${a (<0)}$$ の2乗恨、4乗根、6乗恨、$${\cdots}$$ は、実数の範囲では存在しない(偶数乗して負になる数は、実数の範囲では存在しないため)。
このことは、$${a<0}$$ だと、曲線 $${y=x^n}$$ と直線 $${y=a}$$ の共有点が存在しないことからも分かる。

(case2) $${n}$$ が奇数のとき(ただし $${1}$$ を除く)。
つまり3乗恨(立方根)、5乗恨、7乗恨、$${\cdots}$$ のとき。
実数 $${a}$$ の $${n}$$ 乗恨のうち、実数であるものはただ1つある。これを $${\sqrt[n]{a}}$$ と表す。$${a}$$ が正の実数 $${(a>0)}$$ だと、その $${n}$$ 乗恨も正であり、$${a}$$ が負の実数 $${(a<0)}$$ だと、その $${n}$$ 乗恨も負である。
(例)$${\sqrt[3]{8}=2>0, \sqrt[3]{-8}=-2<0}$$
$${\sqrt[5]{3}>0, \sqrt[5]{-3}<0}$$
実数 $${a}$$ の $${n}$$ 乗恨のうち実数であるものは、曲線 $${y=x^n}$$ と直線 $${y=a}$$ の共有点の $${x}$$ 座標として視覚化される。
一般に $${n}$$ が奇数(ただし $${1}$$ を除く)のときは、$${y=x^n}$$ のグラフは、下図のように原点で接する右肩上がりのグラフになる。それと直線 $${y=a}$$ との交点の $${x}$$ 座標が、$${a}$$ の $${n}$$ 乗恨 $${\sqrt[n]{a}}$$ になる。
$${a>0}$$ のとき

$${a<0}$$ のとき

特に $${a=0}$$ のときは $${\sqrt[n]{0}=0}$$ である。
なお、$${n=1}$$ のとき($${1}$$ 乗恨)は、1乗してその数になるもので、定義よりその数自身になることは明らかなので、普通は考えない。
(例)$${1}$$ の1乗恨は $${1}$$
$${2}$$ の1乗恨は $${2}$$
$${-3}$$ の1乗恨は $${-3}$$
***
(参考1)数の分類
数の分類は以下の通りです。
$$
\begin{align*}
\boldsymbol{複素数 a+bi}
\begin{cases}
\overset{\small b=0 のとき}{\boldsymbol{実数 a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数} \scriptsize{(1, 2, 3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数} \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
{\footnotesize 例 0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize(循環する無限小数)}}\\
{\footnotesize 例 0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
{\scriptsize 例 \pi (=3.1415\cdots) のような \boldsymbol{循環しない無限小数}}\\
{\scriptsize e (=2.7182\cdots) のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0 のとき}{\boldsymbol{虚数 a+bi}} 特に a=0 のとき \boldsymbol{bi} を\boldsymbol{純虚数}という。
\end{cases}
\end{align*}
$$
(参考2)ルート2の発見
最初の無理数の発見は、$${\sqrt{2}}$$ の発見だと言われています。それについて、Wikipedia からの引用です(加筆修正あり) 。非常に恐ろしい物語があります。
(引用始め)
無理数の発見は古代ギリシア文明にまでさかのぼる。一説では、無理数の発見者は古代ギリシャの数学者、ピタゴラスの弟子であるヒッパソスという人物であった。

ヒッパソスは正方形の研究をしているうちに、その辺と対角線の長さの比は整数でも分数でも表せない未知の数、すなわち無理数であることを発見したという。
直角二等辺三角形の辺の比 $${1 : 1 : \sqrt{2}}$$ の、無理数 $${\sqrt{2}}$$ の発見である。

彼の師匠のピタゴラスは、宇宙の万物は数から成り立つこと、そして宇宙を構成する数は、調和した比を保っていると信じていた。

ピタゴラスとその教団は、教義の反証である無理数が存在する事実に動揺し、不都合な事実を隠すため、発見者のヒッパソスを縛りあげ、船から海に突き落として殺害したという伝承が残っている。
またある記述では、ヒッパソス自身は無理数の発見者ではなく、教団が無理数の存在を隠蔽すると決めたその決定に反発し、事実を外部に伝えようとしたために粛清されたとも伝わる。
ピタゴラス教団は、規律違反者は海に突き落として処刑する掟だった。ヒッパソスは教団によって船上からイオニア海に突き落とされ、現在でもそこに眠っているという。
(引用終わり)
(参考3)複素数について
2乗して負になる数は実数の中には存在しません。そこで、2乗すると $${-1}$$ になる新しい数を考えて、これを $${i}$$ と表します。つまり
$$
\begin{align*}
i^2=-1
\end{align*}
$$
この $${i}$$ を虚数単位といいます。
このとき複素数とは、$${a, b}$$ を実数として、虚数単位 $${i}$$ を用いて
$$
\begin{align*}
a+bi
\end{align*}
$$
と表せる数のことです。この $${a}$$ を実部、$${b}$$ を虚部といいます。例えば
$${2+3i}$$($${a=2, b=3}$$ のとき)
$${3-i}$$($${a=3, b=-1}$$ のとき)
$${\sqrt{2}+3\sqrt[3]{5}\,i}$$($${a=\sqrt{2}, b=3\sqrt[3]{5}}$$ のとき)
$${2i}$$($${a=0, b=2}$$ のとき)
$${-\sqrt{3}i}$$($${a=0, b=-\sqrt{3}}$$ のとき)
$${i}$$($${a=0, b=1}$$ のとき)
$${5}$$($${a=5, b=0}$$ のとき)
$${\sqrt[3]{2}}$$($${a=\sqrt[3]{2}, b=0}$$ のとき)
などが複素数です。
複素数のうち、特に $${b\ne0}$$ のときを純虚数といいます。上の例でいえば
$${2+3i}$$($${a=2, b=3}$$ のとき)
$${3-i}$$($${a=3, b=-1}$$ のとき)
$${\sqrt{2}+3\sqrt[3]{5}\,i}$$($${a=\sqrt{2}, b=3\sqrt[3]{5}}$$ のとき)
$${2i}$$($${a=0, b=2}$$ のとき)
$${-\sqrt{3}i}$$($${a=0, b=-\sqrt{3}}$$ のとき)
$${i}$$($${a=0, b=1}$$ のとき)
が虚数です。
虚数の中で、特に $${a=0}$$ のときを純虚数といいます。上の例でいえば
$${2i}$$($${a=0, b=2}$$ のとき)
$${-\sqrt{3}i}$$($${a=0, b=-\sqrt{3}}$$ のとき)
$${i}$$($${a=0, b=1}$$ のとき)
が純虚数です。
また、複素数の中で $${b=0}$$ のときは実数になります。上の例でいえば
$${5}$$($${a=5, b=0}$$ のとき)
$${\sqrt[3]{2}}$$($${a=\sqrt[3]{2}, b=0}$$ のとき)
が実数です。
(参考4)1の3乗根について
$${1}$$ の3乗根(立方根)には、1つの実数の他に2つの虚数があります。これについては、次の記事で詳しく解説しています。
詳しい解説は上の記事にゆずり、ここでは結論のみを述べます。
<$${\bm{1}}$$ の3乗根>
$${1}$$ の3乗根は、次の3つがあります。
$$
\begin{align*}
1, \omega, \omega^2
\end{align*}
$$
なお、$${\omega}$$ とは
$$
\begin{align*}
\omega=\dfrac{-1+\sqrt{3}i}{2} または \omega=\dfrac{-1-\sqrt{3}i}{2}
\end{align*}
$$
のどちらかで定義される虚数の定数です。両者には、プラスとマイナスの違いがありますが
$$
\begin{align*}
\omega=\dfrac{-1+\sqrt{3}i}{2} のとき \omega^2=\dfrac{-1-\sqrt{3}i}{2}\\
\omega=\dfrac{-1-\sqrt{3}i}{2} のとき \omega^2=\dfrac{-1+\sqrt{3}i}{2}
\end{align*}
$$
と、$${\omega}$$ と $${\omega^2}$$ は同じ定数の組み合わせとなるので、どちらで定義してもかまいません。
証明は、3次方程式 $${x^3=1}$$ を解くことによって得られますが、それは上の記事をご覧ください。
これにより、$${1}$$ の3乗根は、複素数の範囲で考えると
$$
\begin{align*}
1, \omega, \omega^2
\end{align*}
$$
の3つになります。そのうち、実数であるものは $${1}$$ のただ一つです。
<実数 $${\bm{a}}$$ の3乗根>
一般に、実数 $${a}$$ の3乗根は、複素数の範囲で考えると
$$
\begin{align*}
\sqrt[3]{a}, \omega\sqrt[3]{a}, \omega^2\sqrt[3]{a}
\end{align*}
$$
の3つになります。そのうち、実数であるものは $${\sqrt[3]{a}}$$ のただ一つです。証明は $${x^3=a}$$ の解として得られますが、詳しくは上で紹介した記事をご覧ください。
いいなと思ったら応援しよう!

