【中学校の数学の知識でユークリッド原論＃005】命題5．二等辺三角形の底角が等しいとき、底辺の下側の角も等しい（証明）【第1巻】

ユークリッド原論は学ぶ意味はあるのか？

中学校2年生の数学の授業で図形の証明を学ぶのですが、ユークリッド原論の内容と何が違うのかというと、一番の違いは式を使わないところです。

ユークリッド原論の内容はすべて文章だけで構成されています。

つまり言葉だけで説明しているんです。

なので、中学校で学んだ数学の知識を持っている人が読むと回りくどいと思う人も多いと思いますが、読めば読むほどなんだか納得してしまうんですよね。

時々、そういうやり方で説明するんだっと思ったり、不可能を説明して可能であることに導いたりと、まだまだ簡単なところしかやっていないのですが、少しずつですが面白いところが増えてきています。

問題を解く面白さというよりかは、知っていく楽しさで、爽快な気持ちというよりかは、理解を深めていくことへの喜びなのかもしれません。

時々、そんな素晴らしい文章を式を使って書き直していることに少々罪悪感を感じながら、でもユークリッド原論を中学校の知識だけで説明することができたら、少しでもユークリッド原論の楽しさを伝える手伝いが出来るのではないかと思っています。

今のところ、第一巻はすべていけそうなので、このシリーズは少なくても48回までは続きそうです。

命題5．二等辺三角形の底角が等しいとき、底辺の下側の角も等しい（証明）

三角形ABCがあり、辺ABが辺ACに等しい二等辺三角形とします。
辺ABを延長したものを線分BD、辺ACを延長したものを線分CEとします。
このとき、角ABCは角ACBに、角CBDは角BCEに等しくなります。

線分AD上の点Bと点Dの間に点Fを描きます。
さらに、線分AE上に
AF=AG
となるように点Gを描きます。

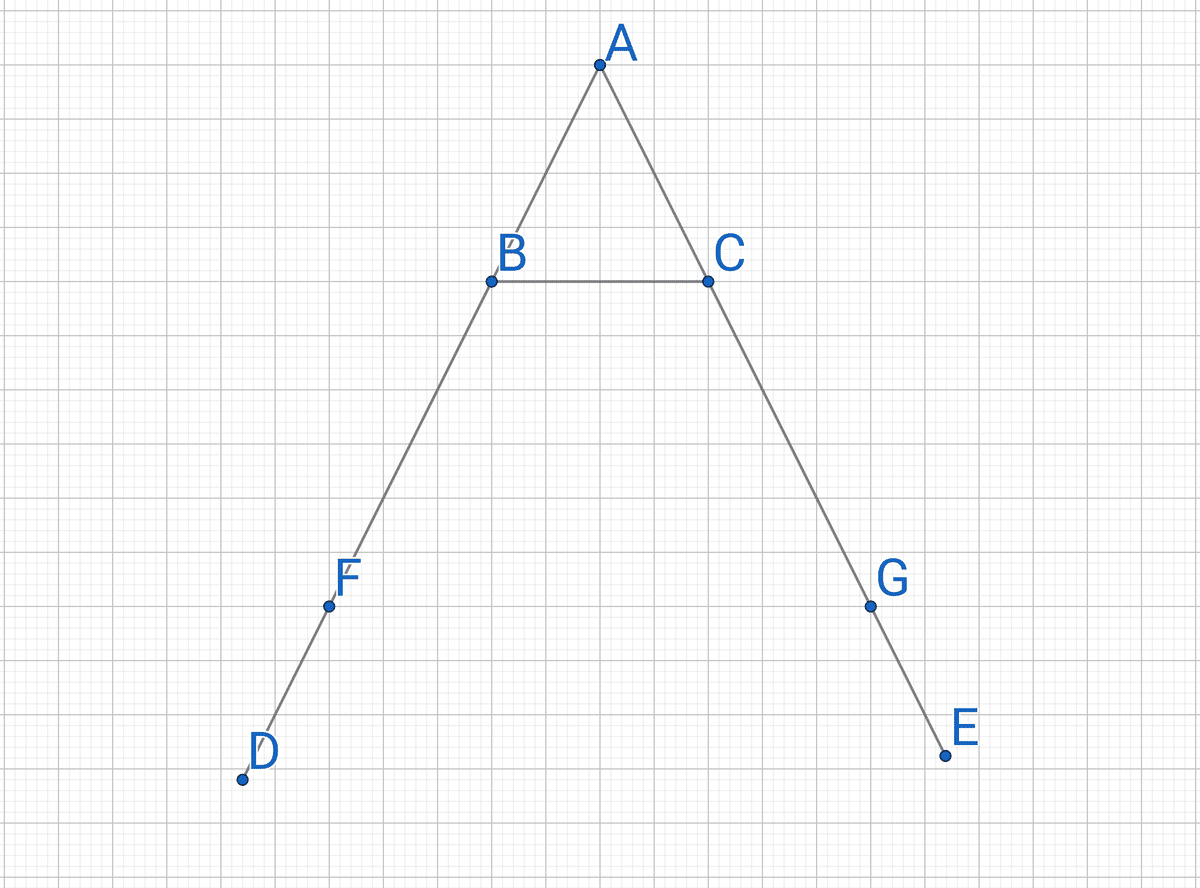
そして、点Cと点F、点Bと点Gを結びます。

そうすると、三角形AFCと三角形AGBにおいて、
AF=AG　・・・①
AC=AB　・・・②
となります。

また、共通の角になるので
∠FAC=∠GAB
となり、命題４より2辺とその間に挟まれた角が等しいとき2つの三角形は等しくなるので
△AFC＝△AGB
となります。

したがって、
∠ACF=∠ABG　・・・③
∠AFC=∠AGB　・・・④
FC＝GB　・・・⑤
となります。

また、
BF=AFーAB　
となり、①と②より
BF＝AGーAC　・・・⑥
となります。

CG＝AGーAC　・・・⑦
となるので、
BF=CG　・・・⑧
となります。

④、⑤、⑧より、命題４より2辺とその間に挟まれた角が等しいとき2つの三角形は等しくなるので
△ＢＦＣ＝△ＣＧＢ
となります。

したがって、
∠FBC=∠GCB　・・・⑨
∠BCF＝∠CBG　・・・⑩
となります。

∠ABC＝∠ABGー∠CBG
となるので、③、⑩より
∠ABC=∠ACFー∠BCF　・・・⑪
となります。

また、
∠ACB＝∠ACFー∠BCF　・・・⑫
となるので、⑪、⑫より
∠ABC＝∠ACB　・・・⑬
となります。

⑨、⑬より、
角ABCは角ACBに、角CBDは角BCEに等しくなるため、
二等辺三角形の底角が等しいとき、底辺の下側の角も等しくなります。