
合成数判定と素数判定⑥(桁数がめちゃ大きい数をエクセル計算で一気に合成数判定する)
合成数判定と素数判定①では、桁数がごく小さい数について、スマホ電卓で手計算で合成数かどうかを判定しましたが、
桁数がめちゃ大きい数について、最終的に、エクセル先生の力を借りて、一括して一気に計算し、合成数かどうかの判定をしてみたいと思います。
最初は導入です。
(1)3318131の場合
合成数判定と素数判定①で展開した
途中式を省略して
$${x=k±\sqrt{k^2-4×3318131}/2}$$
$${x=k±\sqrt{k^2-13272524}/2}$$
エクセル先生による計算結果は
列A:$${k}$$
列B:$${k^2}$$
列C:$${k^2-4×3318131}$$
列D:$${\sqrt{k^2-4×3318131}}$$
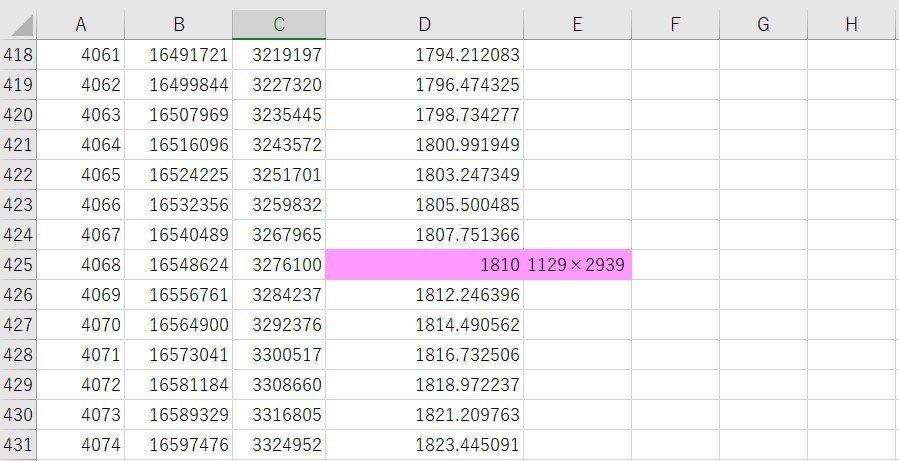
となります。
結果、
$${x=(4068-1810)/2=1129}$$イイ福フク
$${x=(4068 +1810)/2=2939}$$福フクサンキュー感謝
となりました(*´-`)💖
福フクが出て来て、とても嬉しいです
(*´-`)💖💖
(自分で仕込んだんですけど😆)
(2)25297219の場合
途中式を省略して
$${x=k±\sqrt{k^2-4×25297219}/2}$$
$${x=k±\sqrt{k^2-101188876}/2}$$
エクセル先生による計算結果は
列A:$${k}$$
列B:$${k^2}$$
列C:$${k^2-4×25297219}$$
列D:$${\sqrt{k^2-4×25297219}}$$

となります。
結果、
$${x=(10420+2718)/2=6569}$$
$${x=(10420-2718)/2=3851}$$
となりました。
実はこの(2)の数の素因数分解、
NHK「笑わない数学:暗号理論」の回で、“素因数分解が困難”な数字として紹介されたものでした。
東大生のグループがチャレンジしていましたが、かなり手こずっていました。


今回、エクセル先生では、361行目で計算結果が出せました。
この程度の大きさの数だと
“秒殺!”で
エクセル先生の力で計算できますね(*´-`)💖
(3)110061617608331の場合
今回は15桁とめちゃ桁数が大きくなりました。
果たして、エクセル先生では計算ができますでしょうか……
途中式を省略して
$${x=k±\sqrt{k^2-4×110061617608331}/2}$$
エクセル先生による計算結果は
列A:$${k}$$
列B:$${k^2}$$
列C:$${k^2-4×110061617608331}$$
列D:$${\sqrt{k^2-4×110061617608331}}$$

となります。
2万3千818行目に結果が出て
$${x=(21005868-1000010)/2=10002929}$$
イーーー福福フクフク
$${x=(21005868+1000010)/2=11002939}$$
イイーー福フクサンキュー感謝
となりました(*´-`)💖💖💖
ここでも、福フクが出て来てとても嬉しいです
(*´-`)💖💖💖💖
(自分が仕込んだんですけどね😆)
以上となります。
私の合成数判定と素数判定①の方法、アルゴリズムでは
条件が合えば、めちゃ大きな桁数の数でも、エクセル先生の力を借りれば、時間が左程かからず計算することがわかりました。
これ以上の桁数だと、エクセル先生では無理なので、プログラミングして専用アプリを作る必要があります。
また、挑戦して行きます(*´-`)💖
