
Photo by
joyous_eagle810
かけ算計算法 | 格子の方法
はじめに
九九を小学生で覚えたのが、かけ算とのはじめての出会いだろうか?
インドでは、1× 1から20 × 20まで覚えると聞いたことがある。
覚えられたら覚えたほうが早いだろうが、大きな数のかけ算は筆算でいいだろう。
この記事では、「二桁どうしのかけ算」を「格子」を用いて計算する方法について書く。
(1)学校で学ぶかけ算の筆算方法
例えば 15 × 42 ならば、以下のように習ったはずだ。
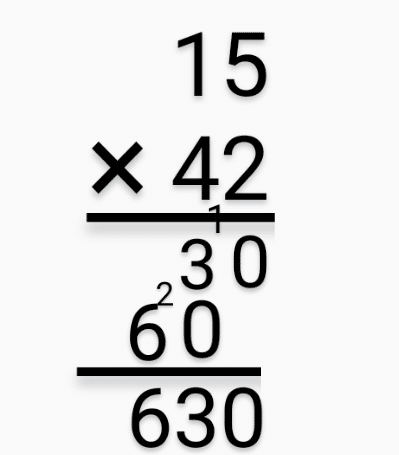
このような筆算で十分だが、繰り上がりの文字を小さく書くので、もしかしたら足すことを忘れてしまうかもしれない。
(2)格子を用いる計算方法

①4つの正方形をかき、対角線で区切る。
②上側と右側に数字をかく。
③上側の数字と右側の数字をそれぞれ一桁ずつ掛ける。
④斜めに足し算する。
原理的には、(1)の縦書きの計算と同じ。
(3)計算が成り立つ理由
筆算の仕方は小学生で習うものだが、中学生で学ぶ「展開・因数分解」の考え方を応用すると分かりやすい。
( a + b ) × ( c + d )
= a × c + a × d + b × c + b × d
さきほどの 15 × 42 ならば、次のようになる。
15 × 42
= ( 10 + 5 ) × ( 40 + 2 )
= 10 × 40 + 10 × 2 + 5 × 40 + 5 × 2
= 400 + 20 + 200 + 10
= 630
むすび
「くだらん」と思った方もいるかもしれない。しかし、小学生の算数は意外と難しい。計算はできても、「なぜ成り立つのか?」と考えると説明できない方も多いと思う。
例えば、今回は扱わなかったが、
400 - 123 の筆算では、何故となりから9を借りてくるのだろう?
説明できますか?
これは宿題にします😄。
数学関連の記事
いいなと思ったら応援しよう!

