三角形の重心を直感的に感じるには。

三角形の重心

三角形の重心G

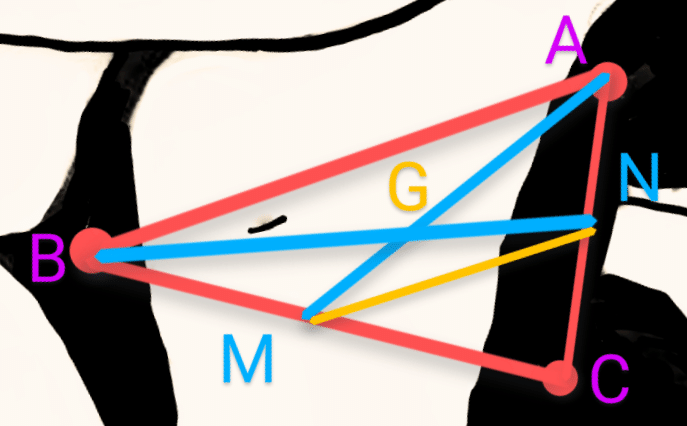
△ABCがある。
辺BCの中点(BM=CMとなる点)をM、
辺CAの中点(AN=CNとなる点)をNとする。

△CABと△CNMにおいて、
CA:CN=2:1・・・①
CB:CM=2:1・・・②
∠ACB=∠NCM(共通)・・・③
①、②、③より
２組の辺の比とその間の角がそれぞれ等しいから
△CAB∽△CNM。

相似な図形の対応する角は等しいから、
∠CAB=∠CNM。
同位角が等しいから、
MN//AB・・・④。
またAB:MN=2:1・・・⑤。

---

△ABGと△MNGにおいて、
∠AGB=∠MGN(対頂角)、
④より、MN//ABだから、
∠ABG=∠MNG(平行線の錯角)。
２組の角がそれぞれ等しいから、
△ABG=△MNG。
⑤より、AB:MN=2:1だから、
BG:GN=2:1、AG:GM=2:1。

このような点のことを「三角形の重心」という。

---

「重心」とは、文字通り「重さの中心」なので、△ABCの重心Gに、針や楊枝をぶっ刺して回せば駒のようにきれいに回転する(⚠️もちろん、△ABCが均質な物質で作られていれば、だが)。

---

　数学的な重心の説明は上に書いた通りだが、なぜ重心Gが重心になるのかということを直感的に理解してみよう。

例えば、次のような「均質な」棒がある場合、どこが重心になるかと言えば当然「真ん中」の点だろう。

重心からズレれば、重いほうに傾く。

では、次のように並んでいる複数の棒をバランスさせるにはどうしたら良いだろうか？

複数の棒になっても、一本の場合と同じで、きれいに並べてそれぞれの棒の中心を支えるように棒(赤い棒)を設置すればよい。こんな感じ(↓)。

じゃあ、こんな感じだったら？

向きが変わっても、やっぱり
それぞれの「真ん中」。

やっぱりきれいに並べて、その「真ん中」を通るように支えれば良い。

---

では、また三角形に戻る。
次のような△ABCがある。

点Aを通るような「棒」(赤い棒、直線、線分)でこの三角形をバランスよく持ち上げるには？

こんな感じ(↓)だろう。

同様に、点Bを通るような「棒」(黄色い棒、直線、線分)で支えるならば、こんな感じ(↓)。

「点」で支えるならば、赤い棒と黄色い棒が交わったところ(点G)になりそうだよね。

実際に点Gのことを「重心」という。

ちなみに点Cと点Gを結ぶ「直線」(線分)をひいて、辺ABと交わる点を「L」とすれば、AL=BLとなる。