
面積を求める
面積とはなんだろうか?
「広さ」と言えば広さだが、思い起こしてみると、一番最初に面積を習ったのは小学生のときだ。
長方形の面積=縦の長さ×横の長さ
最初に「長方形」の面積を習い、そのあと、「三角形」や「円」の面積を習ったが、一番の基本は「長方形の面積」だろう。
今回の記事は(ヘッダーに示した)「二次関数」とX軸の間にできる部分の面積の求め方を考える。


これは、微積分の公式に当てはめれば、
答えは1/3(3分の1)
になるが、
今回は「基本」通り、「長方形の面積」を使って考えてみる。
0から1の区間を2等分すると下の図のようになる。

白い点線で、囲まれた部分の面積は
(1/2)×(1/4)+(1/2)×1=5/8
小数で表すと0.625になる。
同様にして、今度は、0から1の区間を三等分して、長方形の和を求めると次のようになる。

点線で囲まれた部分の面積を求めると
(1/3)×(1/9)+(1/3)×(4/9)+(1/3)×1
=14/27
小数で表すと0.5185.....となる。
次に、0から1の区間を、n等分することを考える。すると、次のようになる。

ここで、( )内は二乗の整数の和だから次のように書き換えられる。
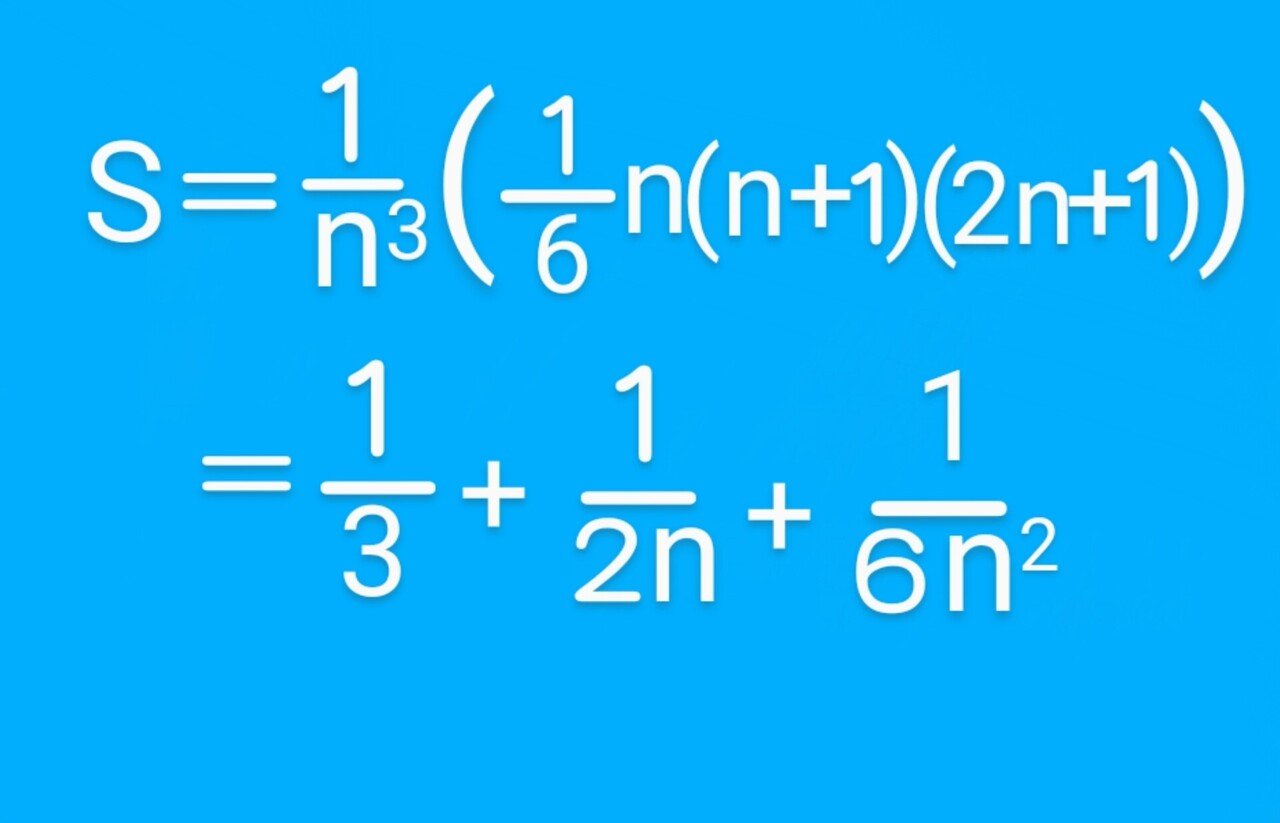
ここで、n→∞にすれば、
長方形の面積の和は1/3となる。
今回は、微積の公式の代わりに、数列の和の公式を使って面積を求めてみた。
いいなと思ったら応援しよう!

