東野圭吾にまなぶ創作術 | 作品を書き続けるために

　東野圭吾。わたしのスキな作家のひとり。ヒット作を連発する作家である。ハマったときには、半年の間、東野圭吾以外の作品を読まないことがあった。
　今でもたまに読むことがあるが、noteを始めて、自分でも文章を書く機会が増えて、「なぜ東野圭吾は多作なのか？」と考えるようになった。
　わたしなりの結論を先に言うと、東野圭吾が多くの名作を生み出す原動力は、たくみに「数学」を用いることにある。どのように数学を用いているか、わたしなりの考えを書く。

　東野圭吾の直木賞作品「容疑者Ｘの献身」に次のような言葉がある。

「石神が数学の試験問題を作る時のセオリーというのがあっただろ。思い込みによる盲点をつく、という話だ。幾何の問題に見せかけて、じつは関数の問題、というやつだ」

東野圭吾「容疑者Ｘの献身」
文春文庫 p 369

　幾何(図形)の問題と見せかけて、関数(代数) の問題であったり、その逆に関数の問題と見せかけて幾何の問題であったりすることがある。もう少し具体的に、どういうことか考えてみよう。

　例えば、中学生の頃に学んだ次のような問題を考えてみる。

「一次関数」っぽい問題だが… …

「弟のPさんは10時に家を出発して、分速◯◯mで、●●m離れた図書館へ向かいました。兄のQさんは10時15分に図書館を出発して、分速✕✕mで家に帰りました。２人の兄弟が出会うのは、家から何m離れたところでしょう？」

解法① ( 関数の問題として解く)

　このような問題は、たいてい、兄と弟の直線の関数( y = ax + b )をそれぞれ求めて、連立方程式を立ててそれを解けば、確実に答えを導くことが可能である。
　この解き方は「代数」的な解き方。

解法② ( 幾何の問題として解く )

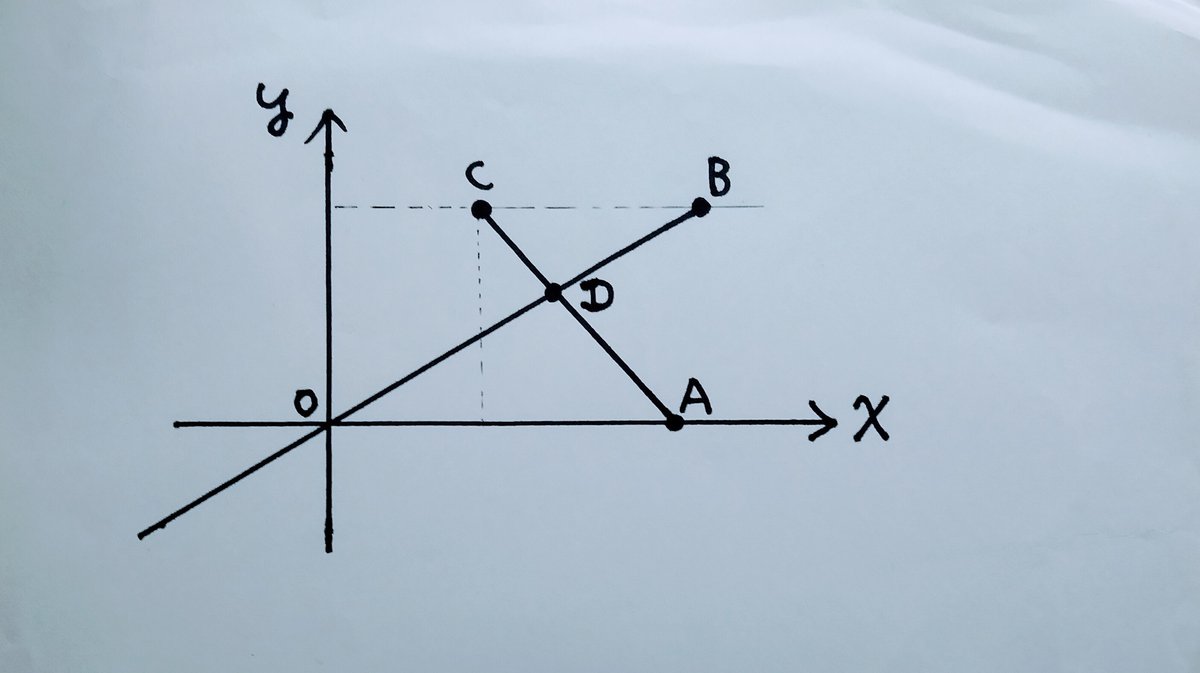
　与えられた値をもとにして、グラフをかいて、「相似」を利用しても解くことができる。
　△OADと△BCDが相似であることに気がつけば、線分OAと線分BCの比が「相似比」になる。家と図書館の距離(高さ)を、それと同じ比で分ける点が交点Dの座標(ｙ座標 )になる。
　この解き方は「幾何」的な解き方。

　このように、同じ問題でも、幾何的な手法でも代数的な手法でも解くことができる。
　今、原点をOにとり、座標軸をかいたが、どこに原点をとってもよい。

　ミステリー小説を書くときも、この手法を用いることができるのではないだろうか？

　座標軸をずらして、犯行時刻を、３時「 🕒️ 」と見せかけて、実は２時「 🕑️ 」だった、というように。
　先ほど例に挙げたグラフの交点近くをボヤけるように描けば、謎解きが難しいミステリーになるだろう。

　例えば、こんなイメージ(↓)。

交点は見えないが… ….

　湯川学シリーズは、本格的なミステリー小説だが、ユークリッド幾何学を非ユークリッド幾何学に置き換えれば、「秘密」のようなファンタジーっぽい作品になることだろう。

　もちろん、実際は、これほど単純ではないだろう。しかし、東野圭吾は元エンジニアの「理系作家」である。
　登場人物の湯川も石神も、わたしには、東野圭吾の分身のように思える。