
力学の基本的な考え方と調和振動子
はじめに
物理を本格的にやったことがない人でも、力学という言葉は聞いたことがあるかもしれません。また、高校物理をやったことがある人にとっては、あまりいい思い出ではないかもしれません。高校物理ではバネ付きおもりの運動や滑車の力のつり合いの問題など、イメージ出来るけどあまり興味を惹かれない話が多いのが一般的です。
とはいえ、力学は物理の基本的な考え方を提供してくれますし、扱う対象が身近なので初めに勉強するにはもってこいの分野になります。とくに、バネ付きおもりの運動については初学者が思っている以上に重要で、物理の分野でどこに行っても出てくるものだったりします。
そこで、力学の基本法則を説明した後に、初等的な問題として知られるバネ付きおもりの運動を紹介します。また、バネ付きおもりの運動が物理学でとくに重要であることを説明します。
力学がやりたいこと
物理がやりたいことは自然現象やモノの性質を明らかにすることですが、とくに力学がやりたいことは物体の運動の様子を定量的に明らかにすることです。たとえば、運動しているボールを考えたときに、そのボールがどんなルールに従って運動しているのか、ある時刻である場所にあったボールは少し時間がたつと元の場所から離れてどこにいるか、といったことを知ることが目的です。
Newtonの運動法則
古典力学はNewtonが大きな貢献をしたのでNewton力学ともいわれています。古典力学の基本法則は以下の三つです。
慣性の法則
運動方程式
作用反作用の法則
1つ目の慣性の法則は、運動する物体は外から力が加わらなければ、いつまでも運動し続けるし、止まっているものは力が加わるまでは、いつまでも動かないという法則です。地球上では空気があるので摩擦が大きく、動き続けるというのは直感的ではないですが、真空中で物体の運動を調べると慣性の法則が成り立っていることが確かめられます。また、電車に乗っていて止まったときに進行方向に倒れそうになるのは自分自身が動き続けようとする慣性のためです。
2つ目の運動方程式は以下の方程式で表されるもので、運動している物体の質量と加速度の積が物体に働いている力に等しいというものです。
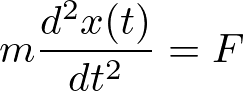
この式をきちんと理解する必要はないですが、気になる方のために記号の説明をしておくとmが物体の質量、d^2x(t)/dt^2の部分が加速度、そのうち、x(t)が物体の座標、Fが物体に働く外力を表しています。また、この加速度の記号は座標の時間に対する2階微分を意味しています。1階微分は座標の時間的な変化率を表していて速度といわれます。したがって、加速度は速度の変化率になっています。
この方程式をx(t)について解くと、ある時刻で物体がどの座標にいるのかがわかることになります。つまり、過去でも未来でも、任意の時刻で物体がどこにいるのかを推測することができるということです。このことから、力学の目標は、性質を明らかにしたい物体に対して運動方程式を立てて解くことであるといいかえられます。
運動方程式を感じられる身近なところいえば、物体の落下現象です。地上で落下する物体は地球からの重力によって引っ張られますが、このときは重力が働き続けるので物体は加速度運動します。実際のところは空気抵抗があるのでどこまでも加速されるわけではなく、物体に働く力と空気抵抗による摩擦力を差し引きした結果、一定の速度で落ちてくるようになります。空気抵抗がないと、雨粒などもすごい速さで落ちてきて危ないです。
3つ目の作用反作用の法則は物体に力を加えると、それと同じ大きさで逆向きに力を加えられる、というものです。たとえば、壁を手で押したときに壁が動かないのは壁が同じ強さで手を押し返しているからです。
これらの3つの法則から物体の運動を定量的に明らかにしていくのが力学になります。
なぜバネ付きおもりの運動が重要か
いきなり難しいことをやろうとすると躓くので、高校や大学で初めに力学を勉強したときには簡単な設定の話から始めることが多いです。そこで代表的なものがバネ付きおもりの運動です。これは壁につながれたバネ付きおもりがあり、水平方向に運動する場合の重りの運動を考えるというものです。

初学者からするとこんな問題は単なる練習問題でしかない、と思う人もいるでしょう。バネが知りたくて物理をやっているわけではなくて、もっと面白そうな電磁気学とか素粒子とかをやってほしいと感じるかもしれません。
もちろん、この問題は初等的ですが、実はそれ以上に概念的に重要です。そのことは物理の勉強を進めていくとわかってきます。おもりは質点(質量があるけど大きさがないもの)とみなすことができるのでバネ付きおもりの運動は質点の周期的な振動現象で、これは調和振動子と呼ばれます。
振動現象は自然界のいたるところで見られるので、それのもっとも簡単なモデルである調和振動子は物理学の概念として非常に重要ということになります。たとえば、水面を走る波を考えると、波は空間的に広がったものですが、水面の一点を見つめるとその点は上下の振動を繰り返しているだけで、その振動が隣の点に伝わっていくことが波であることがわかります。つまり波は調和振動子の集まりで記述できることがわかります。

実際の現象は初等的なモデルほど簡単ではないことがほとんどですが、1番シンプルな例を知っているというのは重要です。なぜなら、簡単な例を拡張して難しい話を考えることができるからです。たとえば、バネ付きおもりの運動を表す運動方程式はF=-kx(t)の場合(kはバネに固有の定数)ですが、これに摩擦項が付いたり、kが時間とともに変化したりする問題も考えることができます。運動方程式を変形させるということは物体に働く物理法則が変わることを意味します。つまり異なる現象を記述できるということになります。
また、調和振動子の重要性は現代物理学を勉強するうえでも効いてきます。
電磁気学をやると、電気・磁気的な力は電場や磁場という空間の電磁気的な性質によって伝わることがわかります。それは電磁波という波として伝わります。通常の意味での電磁気学は古典力学と同じように人間と同じスケールかそれ以上のマクロな立場で物理現象を記述しますが、原子や電子といったミクロの世界では現象を量子力学で記述する必要があります。
ミクロな世界の電磁気学は量子電磁気学と呼ばれ、電子と電磁場は量子的に扱われます。電磁場は空間的に広がったもので、波として伝わるものでしたが、それをミクロな視点で記述するということは、電磁場を量子的な調和振動子のあつまりとして表すことになります。通常、量子電磁気学を学ぶのは理論物理分野の大学院レベルですが、そこまでいくには電磁気学のほかに相対論や熱統計力学やいろいろな理論を勉強しているはずです。そこまで行ってもやっぱり調和振動子が出てくるということです。しかも、この量子電磁気学は物理の理論としてかなり成功していて、物理量の理論的な予測値が実験値とおよそ12桁の精度で一致しています。これは調和振動子の成功であるともいえます。
さらにもうすこし進んで、考えてみます。
自然界には電磁気力のほかに、原子核内部ではたらく強い力と原子核のベータ崩壊という現象を引き起こす弱い力、質量のある物体の間に働く重力があります。量子電磁気学が非常にうまくいったので、同じ仕組みを使って他の力も記述してみたくなるのが物理学者です。この試みは途中まではうまくいっていて、強い力と弱い力は電磁気力と同じ枠組みで記述することに成功しています。これらの3つの力と、力を受ける粒子たちの振る舞いを記述するモデルを素粒子の標準模型と呼び、素粒子物理学の基本的な理論になっています。
調和振動子の考え方を使った理論で自然界で見つかっている力のうち3/4を記述できているということは驚きの事実です。
はじめて調和振動子の勉強をするときに、先の需要まで教えてもらえるとモチベーションが上がると思うのですが、自分の学生時代を振り返ってみるとなかなかそこまでの話は初等的な本には書いていないことが多いです。ほかの例題と同じように扱われているのは少しもったいない気もします。ということで力学で初めに学ぶ調和振動子の重要性を説明してみました。
まとめ
以下が今回のまとめになります。
力学の目的は物体の運動を定量的に明らかにすること
力学の基本法則は慣性の法則、運動方程式、作用・反作用の法則がある。
力学で習う調和振動子の概念は他の物理の分野で非常に大事。
