
資金600万から資産1億円に到達する方法(その4、幾何ブラウン運動で考える)
再び資産600万円から1億円を目指す方法について考えていきます。
「600万円貯金があるけどどうしたら良いかな?1億円目指してFIREしたいんだけど。やっぱ個別株をタイミング見て買うのが良いかな?」、若い友人と相談を受けました。「うーん、どうかな、その方法だと資金を全部溶かす可能性が高いです」と返事をしました。その質問をきっかけに一般投資家にとって最適な株式の投資戦略はなんでしょう?というのを考えてみます。ここまでのメッセージをまとめると下記のようになります。
勝率の期待値が50%を超える投資をする、50%を下回る投資はしない
勝率が高い場合でも1回の投資額を増やすと破産する可能性が高まる
どんなに良い投資でも初期の元本割れは許容しないといけない
元本割れした場合はしばらく元本割れの期間が続くことが多いが投資は中断してはいけない
株価がランダムウォークと考えるのであればテクニカル分析や売り買いのタイミングを考えることは無意味かつ有害である
ランダムウォークで株価のシミュレーションをすることもできますが実際の株価の変動と異なる点があります。例えば実際の株価の増減はその時点の株価に影響されます。すなわち株価が10000円の株式と100円の株式では変動幅が異なります。10000円の株式では1日1000円くらいの変動もありえるが100円の株式では変動は10円くらいまででしょう。そうすると株価の変化はランダムウォークのように現在の株価にある一定の増減を加えるのではなく、ある一定の変動幅で変化すると考えるほうが妥当です。また株価はマイナスになることはありませんがランダムウォークモデルでは株価はマイナスになってしまいます。

import numpy as np
import matplotlib.pyplot as plt
# Define the number of steps
n_steps = 1000
# Simulate the steps: +1 or -1 with equal probability
steps = np.random.choice([-1, 1], size=n_steps)
position = np.cumsum(steps) # Cumulative sum to get the position
# Calculate moving averages
moving_avg_25 = np.convolve(position, np.ones(25)/25, mode='valid')
moving_avg_75 = np.convolve(position, np.ones(75)/75, mode='valid')
# Plot the position over time
plt.figure(figsize=(10, 6))
# Plot position with color based on direction and sign
for i in range(1, len(position)):
if position[i] > position[i-1]: # If the position has increased
plt.plot([i-1, i], [position[i-1], position[i]], 'g-') # Use green
elif position[i] < 0: # If the position is negative
plt.plot([i-1, i], [position[i-1], position[i]], 'b-') # Use blue
else: # If the position has decreased or stayed the same
plt.plot([i-1, i], [position[i-1], position[i]], 'r-') # Use red
# Plot moving averages
plt.plot(np.arange(24, n_steps), moving_avg_25, 'm-', label='25-Day Moving Average')
plt.plot(np.arange(74, n_steps), moving_avg_75, 'k-', label='75-Day Moving Average')
plt.title('Random Walk Simulation with Moving Averages')
plt.xlabel('Step (Day)')
plt.ylabel('Position')
plt.legend()
plt.grid(True)
# Show the plot
plt.show()
幾何ブラウン運動はある意味ランダムウォークなのですが、幾何ブラウン運動においては株価の変動がその時点の株価を基にして変動率が正規分布に従い、そのため株価自体は対数正規分布に従うという特徴があります。そのため幾何ブラウン運動では株価はマイナスになることはありません。これらの特徴を用いるといろいろと興味深い事実が見えてきます。まずランダムウォークから幾何ブラウン運動への導出過程を考えてみます。
ランダムウォークのモデル
ランダムウォークは、次のステップが等確率で上または下に移動する離散時間過程です。この簡単なモデルを用いて、時間が進むにつれて価格(または他の変数)がどのように変化するかをモデル化しています。
幾何ブラウン運動への一般化
幾何ブラウン運動(Geometric Brownian Motion, GBM)は、連続時間の確率過程で、金融市場での株価などのモデル化によく用いられます。幾何ブラウン運動は次の式で表されます。
$$
dS_t = \mu S_t dt + \sigma S_t dW_t
$$
ここで、
$${S_t}$$ は時刻 $${t}$$ での資産価格です。
$${\mu}$$ は資産の平均リターン率(ドリフト項)です。
$${\sigma}$$ は資産リターンのボラティリティ(拡散項)です。
$${dW_t}$$ は標準ブラウン運動(ウィーナー過程)の増分です。
導出過程
離散時間のランダムウォークから始めます:
資産価格の変化を離散時間モデルで表現します。時刻 $${t}$$ での価格を $${S_t}$$、一定の小さな時間ステップでの価格の変化を $${\Delta S_t = S_{t+\Delta t} - S_t}$$ とします。リターンを考慮に入れます:
リターン $${R_t}$$ を、$${R_t = \frac{\Delta S_t}{S_t}}$$ と定義します。このリターンは、ドリフト項 $${\mu \Delta t}$$ とランダムな項 $${\sigma \epsilon \sqrt{\Delta t}}$$ の和としてモデル化できます。ここで、$${\epsilon}$$ は標準正規分布からのランダムサンプルです。連続時間への移行:
$${\Delta t \rightarrow 0}$$ の極限を取ることで、連続時間の過程に移行します。この極限では、リターンの和は積分に、ランダムな変化はブラウン運動の増分に置き換わります。幾何ブラウン運動の式に至ります:
この極限で、資産価格 $${S_t}$$ の対数は、時間に関して連続的に変化し、その変化率は $${\mu}$$ と $${\sigma}$$ に依存します。結果として得られるのが、上記の幾何ブラウン運動の式です。
幾何ブラウン運動を用いた株価のシミュレーションは、ランダムウォークと異なる特性を持ちより実際の株価のシミュレーションに適しています。
幾何ブラウン運動による株価シミュレーション
株価の分布は対数正規分布となる
幾何ブラウン運動を用いると、株価の分布は対数正規分布となります。これは、株価の対数が正規分布に従うということを意味します。対数正規分布では、値が常に正であり、長い尾を持つ可能性が高く、実際の株価の分布により近いモデルを提供します。もし $${S_t}$$ が幾何ブラウン運動に従うならば、$${\ln(S_t)}$$ は正規分布に従います。
幾何ブラウン運動の分布が対数正規分布になる理由は以下の通りです。 1. 幾何ブラウン運動では、各時点での変化率が一定の平均と分散を持つ正規分布に従います。つまり、各時点での変化は相対的な変化率で表現されます。 2. 時間が経過するにつれ、これらの相対的な変化率は乗算的に蓄積されます。例えば、最初の期間に10%増加し、次の期間にさらに10%増加すると、全体では21%の増加になります。 3. 多数の独立な乗算的変化が蓄積されると、中心極限定理により、その積は対数正規分布に収束します。これは、各変化率の対数をとると正規分布に従うためです。 4. したがって、幾何ブラウン運動では、時間経過に伴う資産価値の変化は対数正規分布に従うことになります。
株価はマイナスにならない
幾何ブラウン運動では、株価がマイナスの値にならないのは、株価の変化が株価自体に比例するという性質によるものです。この性質を数式で説明します。
幾何ブラウン運動の確率微分方程式は次のように表されます。
$${dS_t = μS_tdt + σS_tdW_t}$$
ここで、$${dS_t}$$は株価の変化、$${μ}$$はドリフト項(期待リターン)、$${σ}$$はボラティリティ、$${dW_t}$$はウィーナー過程の増分を表します。
この式から、株価の変化$${dS_t}$$は現在の株価$${S_t}$$に比例していることがわかります。つまり、株価が高いほど、株価の変化量も大きくなる傾向があります。
次に、この確率微分方程式を解くと、次の式が得られます。
$${S_t = S_0 \exp\left(\left(μ - \frac{σ^2}{2}\right)t + σW_t\right)}$$
ここで、$${S_0}$$は初期の株価、$${t}$$は経過時間、$${W_t}$$は標準ブラウン運動(ウィーナー過程)を表します。
この式から、株価$${S_t}$$は常に初期株価$${S_0}$$に指数関数を掛けた形で表されることがわかります。指数関数は常に正の値をとるため、初期株価$${S_0}$$が正の値であれば、株価$${S_t}$$は常に正の値をとることになります。
したがって、幾何ブラウン運動では、株価の変化が株価自体に比例し、かつ株価が指数関数で表されるため、株価がマイナスの値にならないのです。これは、株価がゼロ以下になることはないという現実の株式市場の性質と整合的です。
以上の特徴から、ランダムウォークモデルと幾何ブラウン運動モデルは、株価の動きをシミュレーションする際に異なる側面を捉えます。ランダムウォークモデルは、株価の変動を単純化したモデルですが、幾何ブラウン運動モデルでは株価の変動はそのときの株価に応じて変動幅が決まり、株価が常に正の値を取り、実際の市場の動きをより良く反映した分布を提供するためよく利用されています。
幾何ブラウン運動を用いたシミュレーションでわかること
幾何ブラウン運動を用いて株価をシミュレーションしてみます。シミュレーションする際のパラメータ設定は以下の通りです:
初期株価: $${S_0 = 100}$$
平均リターン率: $${\mu = 0.05}$$
ボラティリティ: $${\sigma = 0.2}$$
シミュレーション期間: $${T = 1}$$ 年
これらのパラメータを用いて、幾何ブラウン運動に従う資産価格の動きを100回シミュレーションし、折れ線グラフで重ね合わせて表示しました。各シミュレーションでは、資産価格が時間経過と共にどのように変化するかを観察することができます。
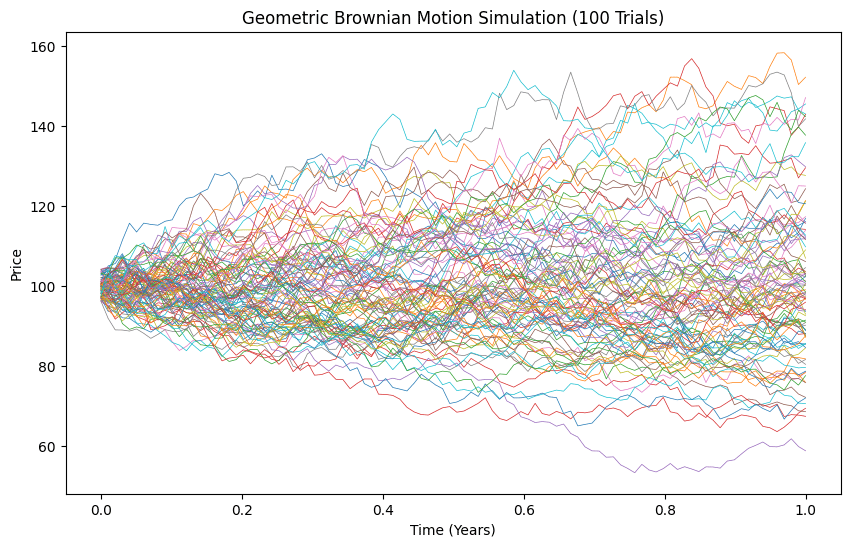
幾何ブラウン運動をシミュレーションする際のパラメータ設定は以下の通りです:
初期株価: $${S_0 = 100}$$
平均リターン率: $${\mu = 0.05}$$
ボラティリティ: $${\sigma = 0.2}$$
シミュレーション期間: $${T = 1}$$ 年
これらのパラメータを用いて、幾何ブラウン運動に従う資産価格の動きを100回シミュレーションし、折れ線グラフで重ね合わせて表示しました。各シミュレーションでは、資産価格が時間経過と共にどのように変化するかを観察することができます。Pythonによるコードは下記になります。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
S0 = 100 # 初期株価
mu = 0.05 # 平均リターン率
sigma = 0.2 # ボラティリティ
T = 1 # 時間(年単位)
dt = 0.01 # 時間の刻み幅
N = round(T / dt) # ステップ数
simulations = 100 # シミュレーション回数
# 幾何ブラウン運動で株価をシミュレート(100回のシミュレーション)
np.random.seed(0) # 結果の再現性のため
plt.figure(figsize=(10, 6))
for i in range(simulations):
W = np.random.standard_normal(N) # 標準正規分布に従うランダム変数
W = np.cumsum(W) * np.sqrt(dt) # ブラウン運動(ウィーナー過程)
time_series = np.linspace(0, T, N)
S = S0 * np.exp((mu - 0.5 * sigma**2) * time_series + sigma * W)
plt.plot(time_series, S, lw=0.5)
plt.title('Geometric Brownian Motion Simulation (100 Trials)')
plt.xlabel('Time (Years)')
plt.ylabel('Price')
plt.show()
この時の株価の分布をみてみます。対数正規分布になっているのですがボラティリティ $${\sigma = 0.2}$$と低いため左右均等のように見えます(分布のほうは100,000回のシミュレーションにしています)。

import numpy as np
import matplotlib.pyplot as plt
# 幾何ブラウン運動のパラメータ設定
S0 = 100 # 初期株価
mu = 0.05 # 平均リターン率
sigma = 0.2 # ボラティリティ
T = 1 # 時間(年単位)
dt = 0.01 # 時間の刻み幅
N = round(T / dt) # ステップ数
simulations = 100000 # シミュレーション回数
# 幾何ブラウン運動で株価をシミュレート
np.random.seed(0) # 結果の再現性のため
final_prices = np.zeros(simulations)
for i in range(simulations):
W = np.random.standard_normal(N) # 標準正規分布に従うランダム変数
W = np.cumsum(W) * np.sqrt(dt) # ブラウン運動(ウィーナー過程)
time_series = np.linspace(0, T, N)
S = S0 * np.exp((mu - 0.5 * sigma**2) * time_series + sigma * W)
final_prices[i] = S[-1]
# 期待値、中央値、最頻値を計算
expected_value = np.mean(final_prices)
median_value = np.median(final_prices)
mode_value = 3*median_value - 2*expected_value # 対数正規分布の最頻値の近似式
# 結果をヒストグラムで表示
plt.figure(figsize=(10, 6))
plt.hist(final_prices, bins=50, alpha=0.6, color='blue', label='Final Prices Distribution')
plt.axvline(expected_value, color='r', linestyle='--', label=f'Expected Value = {expected_value:.2f}')
plt.axvline(median_value, color='g', linestyle='--', label=f'Median Value = {median_value:.2f}')
plt.axvline(mode_value, color='y', linestyle='--', label=f'Mode Value (Approx) = {mode_value:.2f}')
plt.title('Distribution of Final Prices in Geometric Brownian Motion')
plt.xlabel('Final Price')
plt.ylabel('Frequency')
plt.legend()
plt.show()ボラティリティ $${\sigma = 0.4}$$にしてみましょう。先ほどのコードでsigmaを0.4にそれぞれ変えてみます。
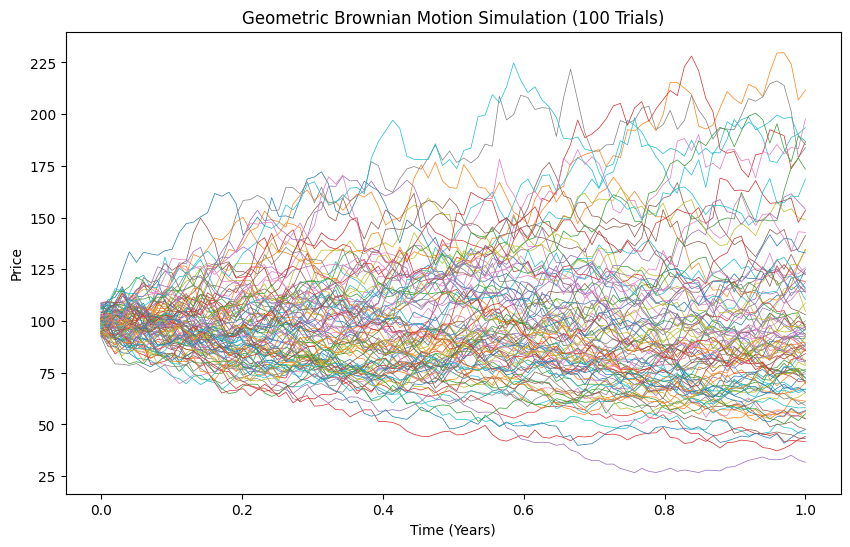

ボラティリティは株価の変動の幅を表しますがこれはリスクと呼ばれることもあります。幾何ブラウン運動で株価をシミュレーションする場合はリスク=ボラティリティです。ボラティリティ(リスク)を変動させていくと期待される株価の期待値、中央値、最頻値はどのように変化していくでしょうか?ここが人間の感覚と異なるところで重要なところです。人間の感覚ではリスクをあげても株価は正規分布する、すなわち期待されるリターンの平均値は同じだが振れ幅が大きくなる、と考えてしまいます。
ボラティリティが高いと株価はどうなる?
ボラティリティ$${\sigma }$$wを0.1~1.0まで変化させたときの株価の期待値、中央値、最頻値はどのように変化するでしょうか?実際にシミュレーションしてみます(100,000回)。

import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
N_simulations = 1000000 # シミュレーション回数
S_0 = 100 # 初期株価
mu = 0.05 # 平均リターン率
T = 1 # 時間(年単位)
# ボラティリティの範囲
volatilities = np.arange(0.1, 1.1, 0.1)
expected_values = []
median_values = []
mode_values = []
for sigma in volatilities:
# 幾何ブラウン運動のシミュレーション
log_returns = np.random.normal(mu - 0.5 * sigma**2, sigma, size=(N_simulations, T))
final_prices = S_0 * np.exp(np.sum(log_returns, axis=1))
# 期待値、中央値、最頻値の計算
expected_value = np.mean(final_prices)
median_value = np.median(final_prices)
mode_value = np.bincount(np.round(final_prices).astype(int)).argmax()
expected_values.append(expected_value)
median_values.append(median_value)
mode_values.append(mode_value)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(volatilities, expected_values, marker='o', label='Expected Value')
plt.plot(volatilities, median_values, marker='s', label='Median Value')
plt.plot(volatilities, mode_values, marker='^', label='Mode Value')
plt.xlabel('Volatility (σ)')
plt.ylabel('Price')
plt.title('Geometric Brownian Motion Simulation')
plt.legend()
plt.grid()
plt.show()ボラティリティを上げていくと期待値は一定ですが中央値、最頻値はどんどん下がっていきます。これは幾何ブラウン運動ですと株価は正規分布でなく対数正規分布するからです。σ=0.1、0.5、1.0の場合の株価の分布を可視化してみます。分布のピークがどんどんとゼロに近づいていることがわかると思います。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import lognorm
# Parameters
sigma_values = [0.1, 0.5, 1.0]
mu = 0.05 # Drift
S_0 = 100 # Initial stock price
T = 1 # Time period in years
S_t_values = np.linspace(0.01, S_0*2, 1000) # Define the range of S_t values for the PDF
# Create a figure for plotting
plt.figure(figsize=(12, 8))
# Loop through each sigma value to plot the PDFs
for sigma in sigma_values:
mu_adj = mu - 0.5 * sigma**2 # Adjust mu for the continuous compounding
pdf_values = lognorm.pdf(S_t_values, s=sigma*np.sqrt(T), scale=np.exp(mu_adj*T + np.log(S_0)))
plt.plot(S_t_values, pdf_values, label=f'PDF of $S_t$ with $\sigma={sigma}$') # Plot the PDF of S_t
# Calculate expected value, median, and mode
expected_value = np.exp(mu*T + np.log(S_0))
median_value = np.exp((mu - 0.5 * sigma**2) * T + np.log(S_0))
mode_value = np.exp((mu - sigma**2) * T + np.log(S_0))
# Plot expected value, median, and mode
plt.axvline(x=expected_value, color='red', linestyle='--', linewidth=0.5, alpha=0.7, label=f'Expected Value ($\sigma={sigma}$)')
plt.axvline(x=median_value, color='green', linestyle='--', linewidth=0.5, alpha=0.7, label=f'Median Value ($\sigma={sigma}$)')
plt.axvline(x=mode_value, color='blue', linestyle='--', linewidth=0.5, alpha=0.7, label=f'Mode Value ($\sigma={sigma}$)')
# Set title, labels, and legend
plt.title('PDF of $S_t$ at T=1 for Different $\sigma$ Values (Real Numbers Scale on Both Axes)')
plt.xlabel('$S_t$')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True, which="both", ls="--")
# Show the plot
plt.show()
横軸を対数軸にしてみます。そうするときれいに左右対称な分布となります。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import lognorm
# Create a new figure for plotting with real numbers scale on y-axis
plt.figure(figsize=(12, 8))
# Loop through each sigma value to plot the PDFs with real numbers scale on y-axis
for sigma in sigma_values:
# Adjust mu for the continuous compounding
mu_adj = mu - 0.5 * sigma**2
# Calculate the PDF of S_t using the log-normal distribution for each sigma
pdf_values = lognorm.pdf(S_t_values, s=sigma*np.sqrt(T), scale=np.exp(mu_adj*T + np.log(S_0)))
# Plot the PDF of S_t
plt.plot(S_t_values, pdf_values, label=f'PDF of $S_t$ with $\sigma={sigma}$')
# Calculate and plot the expected value, median, and mode for each sigma
expected_value = np.exp(mu*T + np.log(S_0))
median_value = np.exp((mu - 0.5 * sigma**2) * T + np.log(S_0))
mode_value = np.exp((mu - sigma**2) * T + np.log(S_0))
plt.axvline(x=expected_value, color='red', linestyle='--', linewidth=0.5, alpha=0.7, label=f'Expected Value ($\sigma={sigma}$)')
plt.axvline(x=median_value, color='green', linestyle='--', linewidth=0.5, alpha=0.7, label=f'Median Value ($\sigma={sigma}$)')
plt.axvline(x=mode_value, color='blue', linestyle='--', linewidth=0.5, alpha=0.7, label=f'Mode Value ($\sigma={sigma}$)')
# Set the plot title and labels
plt.title('PDF of $S_t$ at T=1 for Different $\sigma$ Values (Real Numbers Scale on Y-axis)')
plt.xlabel('$S_t$')
plt.ylabel('Probability Density')
plt.xscale('log')
plt.legend()
plt.grid(True, which="both", ls="--")
# Show the plot
plt.show()つまりボラティリティ(リスク)の高い株価に投資する、ということはより投資の宝くじ的性格が強くなるということです。
極端な例としてσ=2.0という極めて変動幅(ボラティリティ)の高い株価のシミュレーションです(n=1000)。

この場合は83.4%の確率で元本割れします。一部の投資家のみ大きな利益を得るがほとんどの投資家は元本割れしてしまうという結果です。幾何ブラウン運動で考えた時、リスクはなるべく低いほうが良い、ということがわかるのではないでしょうか?
リスクを取りに行く、というと恰好はよいのですが本当に結果がどのようになるかイメージできていますか?
今回のメッセージは”株取引ではリスクはなるべく低いほうが良い”ということになります。
次回は幾何ブラウン運動を用いて実際の株価変動のシミュレーションをさらに詳しく考えていきます。
