
宇宙瞑想:“宇宙の果て”について考える
今回も、非常に些細な日頃の雑念を捨て去り、広大で我々の理解を遥かに超える宇宙の神秘に想いを巡らせる「宇宙瞑想」をやっていきましょう。前回のテーマで「宇宙は膨張し続けている」、「宇宙には始まりがあり、有限の空間である」ということが分かりました(*1, *2)。有限ならば「宇宙の端、辺縁はどうなっているのだろうか」という疑問を持つ人も多いと思います。少年少女の頃誰もが一度は考えたことがあると思いますが、大人になるにつれ日常の雑念の中に埋もれていってしまいます。これについて考えてみます。
・“宇宙の果て”はどうなっているでしょう?
もし我々が超高度の文明を持っていて光の速度を超えて宇宙の果てに到達できるとしたら、宇宙の果てはどうなっているでしょう?
以下に候補として3つのパターンを挙げてみます(図1)。
A.時空が途絶えている(これ以上先に進めない)
B.別の宇宙へとつながっている
C.宇宙の反対側から出てくる
読者の皆さんも自分なりの答えを予想してみてください。
では答えに行く前に2次元空間で考えてみましょう。

・2次元空間での空間の広がり
図2に示すように2次元の世界は前後左右(XY軸)が存在しますが上下(Z軸)の概念が存在しません。図2を見ての通り、この空間は各方向へ無限に広がっているように見えます。ではこのような空間は「無限」に広がっているのでしょうか、それとも「有限」であることも考えられるのでしょうか?もしこの空間の前の方へ延々と進んでいったらどうなるのでしょうか?

・身近な擬似的2次元空間
ここで図2の2次元空間を改めて見るととても見覚えのある光景に見えます。図3の左側に示されるように、我々が普段よく見る光景は2次元空間のような広がりを持ちますし、我々が普段使う地図も2次元表示です(図3右)。つまり、地球規模のマクロな視点から見ると高層ビルも地下街も誤差レベルの微々たるものですので我々はほぼ地球の表面でしか生活していない、つまり「地球の表面は擬似的な2次元空間世界」と言えます。

・地球表面を2次元空間と考える
では地球表面を擬似的な2次元空間と考えると、一見地面は地平線が見えるほど遥か遠くに続いていますし、海も水平線が見えるほど果てしなく遠くまで続いています。ただし、これが無限に続いているかというとそうではありません。もしジェット機でどんどん先へと進んでいくとどうなるかというと、現代人は誰もが知っていることですが自分が出発した地点と反対方向から戻ってくることになります(図4右)。
そしてこの地球表面の2次元空間は「有限」な空間ですが「果て(辺縁)」は存在しません。どこまでも進み続けることができますが、同じところをループし続けて辺縁に辿り着くことはありません。図4左はこの2次元世界を展開した地図ですが黄色矢印と青色矢印は2次元空間的には離れていますが実際は継ぎ目もなく連続していることが分かると思います。

・2次元の人間は球面を知覚できるか?
私達は元々3次元の世界の住人なので球面が湾曲していたり、平らに見える地面も実際は地球という球体であることを知っています。それでは仮に2次元世界に住人がいた場合、「立体」や「3次元」という概念のない彼らに「平面が曲がっていること」「球体の表面であること」を知覚したり理解することが可能なのでしょうか?
2次元世界からすると曲げたり歪んだりしても3次元的な概念を持たない彼らにはそれを知覚する術が無いように思われます。しかし2次元世界にいながら3次元的な変形を把握する方法も実はあります。例えばその一つは「3角形の内角の和」でも表されます。
誰もが「3角形の内角の和=180°」だと思っていて「それ以外にあるのか?」と思う人もいるかもしれません。しかしながらそれは「まったく歪みのない完全な平面」でのみ成り立つ法則です。
平面の曲率には「+」「−」「±0」の3パターンあり、曲率によって三角形の内角の和が180°よりも大きくなったり小さくなったりします(図5、*3)。例えば、“日本と北極点とエジプト”の3点を最短距離で結んだ3角形の内角の和はどうなるかというと図5Aのように180°より大きくなります。なので、もし3次元を知覚できない2次元の住人がいたとしても広大な規模で角度を検出することで「自身が存在する2次元空間が平坦か曲がっているか」を知ることが可能です。

・3次元的な空間がループする場合どのような構造になるか
図4の左の平面地図の端と端を合わせると図4右のような球体の地球になります。それと同じように、今度は3次元空間の端と端をつなげるように想像してみましょう。図6にそのイメージを載せていますが、まず我々の存在する空間の端と端(図6AとA')を合わせると円筒状になります。そして同様に開いた端と端(図6BとB')を合わせるとドーナツ状の構造体になります(図6右下)。この構造が「トーラス(*4)」と呼ばれる構造です。基本図形を一枚の平面のように表していますが、実際は3次元空間を表しています。そしてトーラス構造(図6右下)は3次元より高次元から見た構造と考えられています。

・3次元世界から高次元の構造を観測するには
3次元を直接知覚できない2次元世界から時空の歪みを検知するには3角形の内角の和を計測してみるというのが2次平面の曲率を求める一つの方法でした。では3次元空間の曲率を知るための方法としては、その一つに「宇宙背景放射(CMB, *5)」という宇宙の原初の光を調べる方法があります。これは探査人工衛星COBE(1989-)、WMAP(2001-)、Planck(2009-)といった衛星で宇宙のごく初期の光を全方向から計測し、これを基に宇宙のさまざまな情報を解析するという手法になります。

この宇宙背景放射の“2点相関関数”を解析すると、この宇宙は「ほぼ平坦な(曲率の少ない)トーラス構造」つまり、対極にある時空の端がつながっている構造である可能性が高いことが最近の研究で示されています。さらにそのトーラス(繰り返し構造の基本単位)の大きさは観測可能な宇宙サイズ(光速×ハッブル時間=約138億光年)の3〜4倍程度(400〜500億光年)である可能性が高いとされています(*6)。
・宇宙は「トーラス」構造
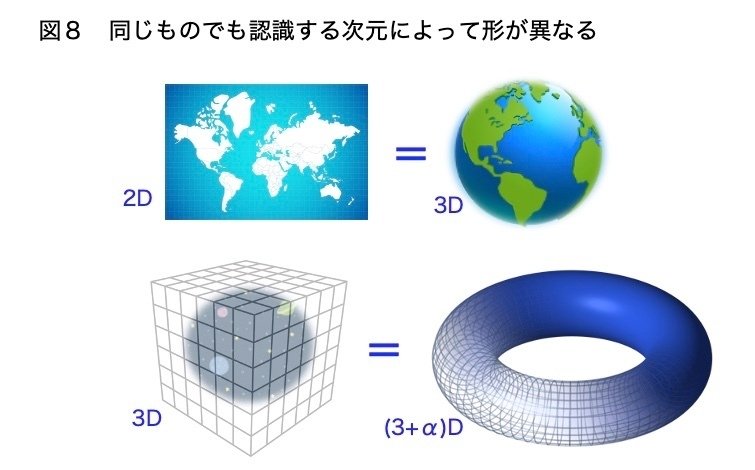
我々は生活範囲において地面はどこまでいっても平坦な構造と感じています。ただし、マクロな視点で見ると正の曲率をもった有限の球面であり、進み続けるといずれは元の場所へと戻ってきます。つまり地球で考えると「有限ではあるが地面や海面が途絶えたりはしていない」、「どこまでも無限に進める(周回できる)が、他の惑星に辿り着くことはない」、そして「ある方向に進み続けると反対側から現れる」という空間に我々は存在しています。図8上のように、平面ではあるが端がつながっていて終わりのない面を形成しています。
宇宙も同じような構造と考えられていて「対極の時空がつながっている」、図8下のように我々が知覚する宇宙は3次元空間であるが、より高い次元で宇宙を見ると図8右下のようにドーナツのようなトーラス構造をとっている可能性が高いようです。
・最初の問題の答えとは
最終的に最初の問いの答えとしては、“宇宙の果て”は「急に時空が途絶えてしまうわけではなく」、「別の宇宙へとつながっているわけでもなく」、「いずれは反対側から元の場所へ戻ってくる」、つまり現代の宇宙論から推察すると図1の中では「C」が最も現実的と考えられます。予想通りだったでしょうか、それとも意外な答えだったでしょうか?
・次元を認識し知覚するには
我々は肉体を持ち、3次元の宇宙の中で生活しています。我々の身体は細胞、タンパク質、アミノ酸、分子、元素、素粒子、いずれのレベルにおいても「物質」で構成されており、3次元の物理法則に支配されている「肉体」は別の次元へ移動することはできません。ただし、我々が保持しているものの中で「物質」ではないものがあります。これまでの記事を読んでいる読者の方々ならもう気付いていると思いますが、そうです、我々の「意識」です。意識は形を持たず物質的な側面を持ちません。つまり、次元の壁を越えられるツールの一つなのです。
ただし、会社勤めや知人との雑談、家庭の雑事といった日常生活において「次元」を意識することは“絶対に”ありません。「次元」を知覚し認識するための方法が「瞑想」です。他の次元を知覚するには「この3次元の現実世界からのあらゆる刺激を遮断する」必要があります。少しでも3次元現実世界のことを考えた瞬間にあなたの意識は「いつもの日常の意識」に引き戻されるでしょう。そうならないためにはある程度の鍛錬が必要です。意識も使い方次第では「日々の雑事の心配とストレスを生み出すだけのツール」にもなれば「次元や宇宙を超越できるツール」に鍛え上げることも可能です。そして「瞑想」が意識の変容だけでなく身体にも良い効果をもたらすことは過去の記事でも取り上げている通りです(*7)。

・次元を超えた世界の学問=形而上学
今科学は観測できる範囲を超え、その先にあるものを推測し解析する段階になっています。しかしそれは最近に始まったことではなくアインシュタインの時代には既に「まだ科学的に発見されてないものを提唱する」ということは行われていました。科学では扱えない“形のない、常識的に捉えられないもの”の学問として「形而上学(けいじじょうがく)」があります。そしてこの3次元を超えた4次元以上の概念も「形而上学」では何世紀も前から伝えられていることであり、アインシュタインも形而上学に精通していたと言い伝えられています。「形而上学」は自然科学を超えた真の世界を理解する一助となり、「瞑想」は3次元にいながら4次元以上の高次元を知覚する良い方法となるでしょう。ぜひ日々の瞑想習慣を取り入れていきましょう。
(著者:野宮琢磨)

野宮琢磨 医学博士, 瞑想・形而上学ガイド
Takuma Nomiya, MD, PhD, Meditation/Metaphysics Guide
臨床医として20年以上様々な疾患と患者に接し、身体的問題と同時に精神的問題にも取り組む。基礎研究と臨床研究で数々の英文研究論文を執筆。業績は海外でも評価され、自身が学術論文を執筆するだけではなく、海外の医学学術雑誌から研究論文の査読の依頼も引き受けている。エビデンス偏重主義にならないよう、未開拓の研究分野にも注目。医療の未来を探り続けている。
引用/参考文献:
*1. Hubble E. A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Sciences, vol. 15, no. 3, pp. 168-173, 1929. https://doi.org/10.1073/pnas.15.3.168
*2. 宇宙瞑想:“宇宙は永遠か?”について考える
https://note.com/newlifemagazine/n/n4985749ff8b6
*3. Cosmic Topology
http://www.scholarpedia.org/article/Cosmic_Topology
*4. トーラス−Wikipedia
https://ja.wikipedia.org/wiki/トーラス
*5. 宇宙マイクロ波背景放射(CMB)ーWikipedia
https://ja.wikipedia.org/wiki/宇宙マイクロ波背景放射
*6. Aurich R, Buchert T et al, The variance of the CMB temperature gradient: a new signature of a multiply connected Universe, arXiv:2106.13205 [astro-ph.CO], 24 Jun 2021, https://doi.org/10.48550/arXiv.2106.13205
*7. 瞑想、脳、幸せホルモン…医学目線の本当の話
https://note.com/newlifemagazine/m/mb580e4b26aa4
画像引用:
いらすとや https://www.irasutoya.com/
https://www.freepik.com/premium-vector/
https://www.pexels.com/photo/
https://www.free-world-maps.com/physical-free-world-map-b1
https://www.kyoto-su.ac.jp/project/st/st17_01.html
https://ja.wikipedia.org/wiki/ガウス曲率#/media/ファイル:Hyperbolic_triangle.svg
https://ja.wikipedia.org/wiki/トーラス#/media/ファイル:Torus.png
https://pixabay.com/illustrations/the-fourth-dimension-fractal-2727090/
https://www.adobe.com/jp/products/firefly.html
前回までの関連記事はこちらから
※引用文献の内容に関する著作権は該当論文の著者または発行者に帰属します。
※当コンテンツに関する著作権は著者に帰属します。当コンテンツの一部または全部を無断で転載・二次利用することを禁止します。
※著者は執筆内容において利益相反関係にある企業等はありません。

★LINE友達限定情報、毎週金曜に配信中★

銀河レベルのぶっちぎりに新しい情報で、
誰もが本質を生きる時代を目指します。
更新情報はライン公式でお知らせしています。
