
数学の先生がカードゲームを作った話
アイデアもカードも、すべてオリジナル。
中学2年生の1次関数が学べるカードゲームです。
ゲーム名は関数大富豪。


【用意するもの】
カード48枚(16種類×3枚ずつ)※名刺サイズに印刷してラミネートする
プラスマイナス サイコロ(目はー3,-2,-1,1,2,3)

【ルール】
大富豪のルールである。順番にカードを場に出していき、手札がなくなったものから勝利となる。
4人班で行う。
カードの数値の大小はyの値によって決まる。例えばy=1とy=2のカードでは、y=2の方が数値は大きい。
じゃんけんをして勝った生徒からゲームスタート。
その勝った生徒が、ゲームスタート時にサイコロを振り、出た目をxの値としてゲームを続ける。(サイコロははじめの1回だけふる。順番に振ることはない)
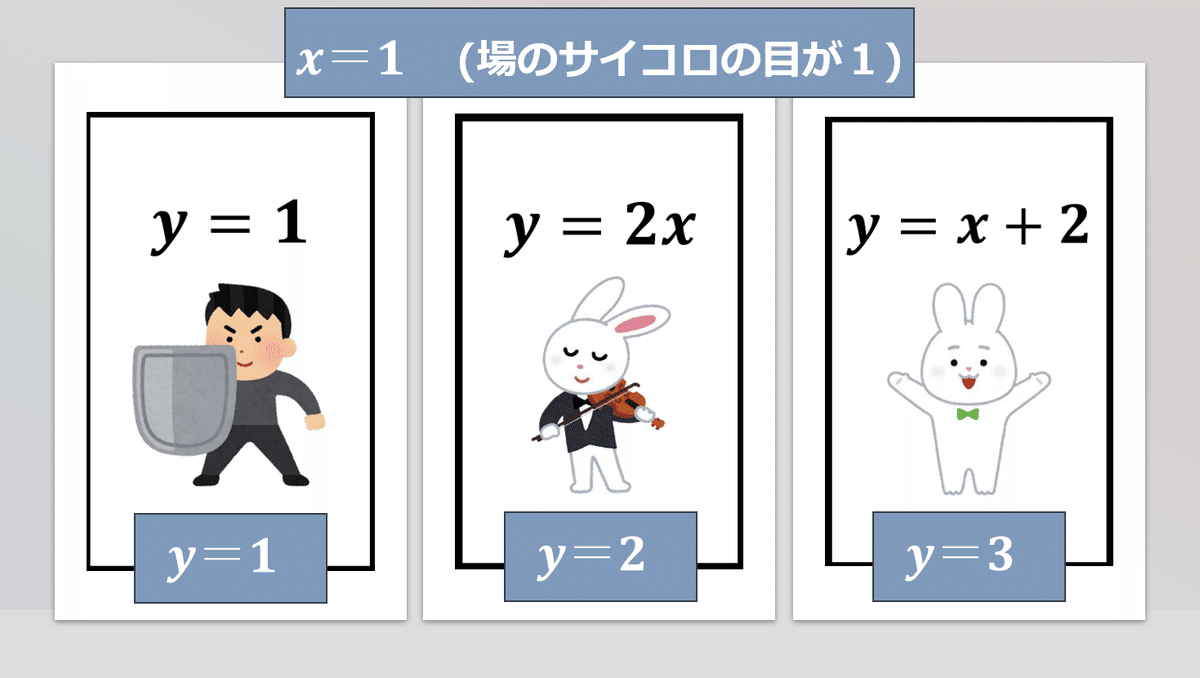
場に出ているサイコロの目はxの値。つまり、場に出ているサイコロの目によって、カードの数値が変わる。以下の3枚のカードを例に説明する。

もしxの値(サイコロの目)が1ならば、下の図のようになる。x=1を式に代入して、yの値を求めるのだ。x=1のときは、3枚のうち、y=x+2が最も強いカードとなる。
もしxの値(サイコロの目)がー2ならば、下の図のようになる。この場合、3枚のうち、y=1 が最も強いカードとなる。

【このゲームのポイント】
なんといっても 手札のカードが、場のサイコロの目に左右されて強くもなったり弱くもなったりするところだろう。xの値にかかわらず、yの値が決まっているカードは安定感がある、というのも遊びながら学べる。
否が応でも計算を頭の中でしなければ ゲームができないのは、数学の授業らしいゲームともいえる。
ゲームの味付けとして、場のサイコロの目を変えるカードも用意した。

このカードを上手に使うことで、手札の腐っているカードを輝かせることができるのだ。案外頭を使うゲームである。
ちなみに、xがー3以上3以下の整数(0を除く)のとき、ゲームが盛り上がるyの値を分析して、カードの関数を決めた。分析にはPCでグラフを描いてみて、xの値に対応するyの値の大小を比べてみた。

■数学の先生の悩み
数学の授業では、生徒に例題を教えて、演習させる型がほとんどだが、その授業形態は令和の教育にはフィットしないのかもしれない。
学習塾に行って、中学校の先生が教える内容を「すでに知っている」と思って話を聞かない生徒。算数・数学が苦手で、1対多数の講義形式では理解が難しい生徒。これらの生徒が混在している教室では、一斉に同時に授業をしても教育効果は薄い。
令和の時代、授業をしてもあまり手ごたえを感じない数学の先生ってけっこういると思う。
■だからゲームを作った。
上に挙げた両者のタイプの生徒の感情が動くような授業の手法はゲームだと思う。
ゲームは楽しい。数学が苦手な生徒でも取り組みやすいし、ゲームだと、学力が高い生徒が 数学に苦手意識をもっているクラスメイトに自然にサポートできる仕組みが生まれる。
学習塾では味わえない価値を生み出そうとするのは公立中学校の教員のプライドである。だから僕は、カードゲームを作った。
ゲームを作る側に回るのは楽しかった。ゆくゆくは生徒にゲームを作らせてみようとも思う。

