
【高校数学】漸化式の解き方が謎
皆さんこんにちは!
日常の中で様々なことに疑問を持ち、学んでいっているのですが、せっかくなのでそれを発信していき、共有していこうと思っている、そんな企画でございます。
今回は数学Bの漸化式についてです。
①漸化式の解き方は習ったけど、どうしてそうやって解くの?
②途中で出てくる特性方程式のαって何なの!!
といった質問に答ていきたいと思います、が
②の特性方程式のαについてまで書き出すとややこしく、長ったらしくなってしまうため、今回は①の一番基礎的な漸化式の解き方のみを解説していきます。
特性方程式のαについてこちらの記事をどうぞ
抑
まず漸化式ってなんやねん!って話ですよね?
「私、数学アレルギーなの~。数字見るだけでほんとムリ。蕁麻疹出ちゃう~」という文系女子を黙らせる一撃
"漸化式"
・・・読めない
これは「ざんかしき」であってるの?
斬も暫も「ザン」でしょ?
からの
まさかの「ぜんかしき」
「そんな…唯一取り柄だと思っていた漢字すらできないなんて…」
そういって散っていった人も少なくないはず。
「漸」って何ですか?
調べてみると・・・
漸・・・ゼン・ようや(く)
意味:ようやく、しだいに
こんな感じでした。
「ようやく」って漢字で書くと「漸く」なんですよ!
漸化式っていうのは
前の項が決まると次第に次の項も決まっていく式
みたいな意味になります。
(ちなみに、数学には他にも「漸」を使った言葉が出てきて、
それが「漸近線」。
グラフが次第に近づいていく線のことですね。)
そして、この漸化式は次のように解いていくと習います。
解いてみるぞ!!
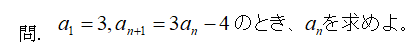
わぁー、いやな奴だ…
仕方がない、授業で習ったとおりにやってみよう…
えーっと、まずは「特性方程式」ってやつを解くんだったな。
![]()
こんな感じだった気がするな・・・
![]()
まぁいいや。
そうすると、α=2だから…
その後どうするんだっけ?
![]()
何でこの形に式変形するのかはわからないけど、
たしかこの形に直すはずだ・・・
α=2だったから、
![]()
こんな形になって、
あ、そうそう。
![]()
として考えて、等比数列みたいな形になった気がするな。
お!すごい!!できたぞ!!
ちょっとモヤモヤしたところはあるけど・・・
よくできました
皆さんは解けましたか?
受験を控えた高校生は結構正答率高かったのではないでしょうか?
さて、今問題を解いていた彼は問題が解けたにもかかわらず、2つの疑問を持ってしまいました。
疑問①

疑問②
先ほども言ったように、疑問②は別に記事を作成し、そちらで解説しています。
ここからは疑問①を考えていきましょう!
漸化式の常識
まず大前提なのですが、
基本的に漸化式を解くことはできません。
答えが出る漸化式はかなり特殊な例です。何でかはわかりませんが、きっと何か理由があるのでしょう。
「学校で習った漸化式は全部解けてるぞ!」
ってそりゃ解けない漸化式教えても仕方ないから解けるものだけ教えますよ。
そんな中、東大に行くような頭のいい人たちは工夫を積み重ねて解く方法を考え出してきました。
その特殊な解法で解ける漸化式のみを高校の授業では取り扱っています。
「じゃぁ、解けない漸化式ってどんなやつなの?」
と疑問に思う方もいるかもしれませんが、ぜひ自分で調べてみてください。
残念ながら僕にそこまでの知識はありません。。。
(a_nが関数の中に入っちゃったりすると難しくなると思います。)
んで、その特殊な解法の内の一つが特性方程式を用いた解法です。
謎の式変形
では、改めて本題に参りましょう。
解読不能な問題を渡されたときは見たことある形に直してみるのが基本!
明日のMTGのアジェンダを作るためにゼロベースからエビデンスを集めたいといけないんだよね。いやぁー、最近のインフルエンサーはほんと凄いわ!まじで価値観変わる!
こんな難問出されたら即降参ですよね。
でも、ちゃんと一つ一つの単語を見たことある単語に置き換えれば何となく言いたいことは理解できると思います。
MTG→ミーティング(会議)、アジェンダ→議題 みたいな感じ
それと同じことを数学にも適用してやるのです。
(数学、というか問題を解く上での基本!)
で、大事なのは「じゃぁ、見たことある形って何なの?」
ということなのですが、
そこでこの形を考えます。じゃんっ
![]()
これ、意味わかりますかね?
これだけ見せられても
「だから?」って感じになってしまいますが・・・
でも、よくよく考えてみてほしいのです。
3番目の項は2番目の項のp倍、4番目の項はさらにそのp倍…
となっていく姿を・・・
これって等比数列なんですよね。
![]()
「えぇ!?等比数列これ(↑)やん!!」
と思うかもしれませんが、意味は同じなんですよ。
それも知りたい人は⇩をご覧ください。
興味ない方は飛ばしてください。
補講
![]()
まずこれ。
次の項(n+1)に行きます。
![]()
nがn+1になったのでrに乗ってるnも増えてますね。
![]()
rの上を整理しましょう。
![]()
整理した直後ですが、rを1人だけ外に出してみます。
![]()
ちょっとrの位置を変えてみました。
ここで注目なのですが、
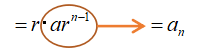
右の部分って今こうなってるんですよね。
なんと、一番最初の式に戻ってるのです!
アニメも数学もループものが人気
だから
![]()
この形になって、これっていうのは
![]()
最初に気になっていた部分のpがrになっただけですね。
(パソコン上で説明するのは非常に難しいですね。。。わかりにくかったらすみません。)
解けないはずの問題を解く
で、改めて問題の式を見てみますが、
![]()
この式の定数項、「ー4」が無ければ
![]()
これみたいな形になり、先ほども書いたように、等比数列の知識を使って解決できることになります。
![]()
突如現れたこの謎の式変形はそういった考え方から生まれたものだったわけです。
![]()
と思われた方もいるかもしれませんが、
![]()
こうすることで先ほどの式は
![]()
こう見ることができて、見事bの等比数列だということができますね。
「え?ちょっと待って。
そこが意味わからない。」
という方は⇩をご覧ください。
興味ない方は飛ばしてください。
補講2
![]()
という意味です。
そして、
![]()
としたので、
![]()
ということになりますね。
では、ここで
![]()
という数列を考えてみましょう。
この場合、
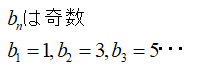
ここで、ちょっと崩してやって、
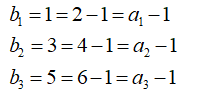
これがずーーっと続いて、最終的には
![]()
こんな感じになることが分かります。
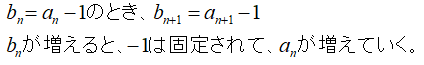
てなわけで、
![]()
ということが分かり、
![]()
これを
![]()
こう書き換えることができるって分かりました。
めでたしめでたし
(わかりづらい・・・)
等比数列ならひとりでとけるもん
無事、解けなさそうな数列を見たことのある数列に置き換えることができて一件落着。
普通の等比数列だとわかれば公式も知ってるし、あとは一人で解けそうです。
でも、ちょっと待って!
こんな無理やりなことしちゃっていいの?
皆さんは
![]()
という理想的な式を作って問題を解けるようにしちゃおう!
ってやっちゃったわけです。
このαって何よ!って話ですよね。
彼氏の家に遊びに行ったら見たこともない女が当たり前のようにソファでくつろいでたら誰だって違和感を覚えるでしょ。
そんな悩める皆さんを助けるのがご存じ「特性方程式」
このαの正体を見破っちゃおうって式でございます。
![]()
これですね。
この特性方程式を解くことでαが分かり、そのαを使うことで解けない漸化式が解いたことのある等比数列になり、答えが導き出せるというわけです。
おしまい

漸化式っていうのは頭のいい人がひらめいた解けない式を解く工夫をすることで解決できたのです。
ずべこべ言わずにその恩恵にあやかりましょう。
「なんでこうなるねん・・・」
と思っていた方々の多くはこの記事を見て
「結局どういうことやねん・・・」
ってなったと思います。
まぁとにかく「なるものはなる!」ってことです。
とりあえずそういうもんだと暗記しちゃいましょう。
それでも余裕ができた人は、改めて「なぜ漸化式はこうすると解けるのか」ということを考え直してみてほしいです。
かく言う僕もその一人です。
改めて考え直してみて、何となく納得できたようなできなかったような・・・
といった感じです。
それで、何度も言っていますが、
漸化式を解く上で「特性方程式」なるものが出てきて、
こいつもぱっと出の新人なのに全く自己紹介なく一軍入りしてきやがります。
こちらの記事です。二つ合わせて一つのお話になると思います。
ということで今回はここまで。
今回の記事がためになったという方、面白かったという方はぜひSNS等でシェアしてくださると嬉しいです。
また、「お疲れ!コーヒーでも飲みな!」という方はサポートをしてくださるととても励みになります!
それでは、また次回の記事でお会いしましょう!!
