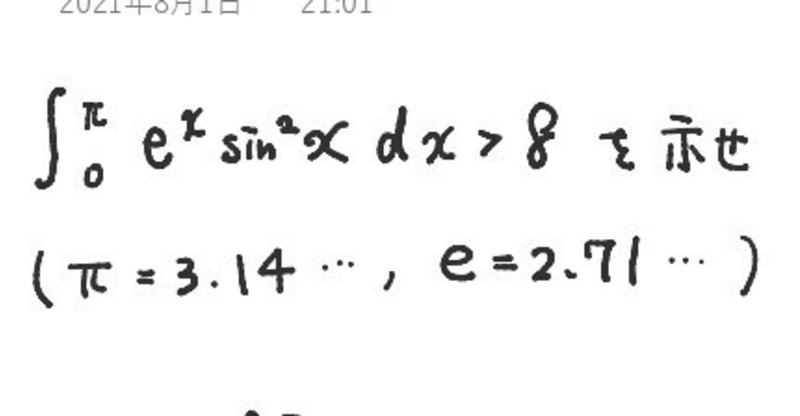記事一覧
添削課題(微分積分⑫)_三角関数の積分x=tanθ/2とおく解法
初投稿から1年経ち、1万PVを達成した。これからも一緒に数学を学んでいきましょう。
典型的な問題であるが、初見はきついだろう。
このようなタイプは必ず誘導が付くので、流れに乗りながら完答したい。
添削課題(微分積分⑪)絶対値のついた関数の積分
ついに紆余曲折あったオリンピックとパラリンピックが閉幕した。
結局、ほとんど見ることはなかったなあ。
計算自体は平易なものである。あとは平方根の処理の仕方と絶対値の外し方は数学1の知識である。(2)については、αの具体的な値が分からずとも定積分の値を出すことができる典型的な問題である。
定積分や面積計算で頻繁に難関大で出題されるので、類題を参考書を使ってやっておきたい。
添削課題(微分積分⑩)山口大・理-後_最小2乗法※修正版
基本的な計算を問われている。(2)は展開する前に被積分関数xの他に変数aがあることを確認しよう。その際、xは数字に置き換わるが、aは残る。
つまり、aの二次関数になるということを見抜いておくとよい。
添削課題(微分積分⑨)部分積分の基本計算プリント
部分積分の計算はできるとかなり得点源になるので、しっかりできるようにしたいところ。今回は、その基本計算をまとめてみた。
この部分積分をマスターしておけば、数Ⅱの面積計算、特に共通テストでの時短テクニックとなる。
以下に有名な6分の1公式などをまとめたサイトのリンクを貼っておく。是非、部分積分を用いて証明してみよう。
添削課題(微分積分②)微分の定義_弘前大
微分の定義は生徒にはやや不人気であり、定着率が悪い気がする。
平均変化率とは、割線の傾きであり、
微分係数とは、接線の傾きであり、
導関数とは、接線の傾きを表す関数であり、
微分とは、導関数を表すことである。
このあたりを誤魔化して計算だけしてきた者は、入試問題にて地獄に突き落とされることになるだろう。1つ1つ丁寧に押さえておくことが、遠回りのようであるが近道なのだ。
学問に王道なし