
相対性理論の「時間の遅れ」の数学
相対性理論のいわゆる「時間の遅れ」に関して、学生からこんな質問をされたことがあります:
「止まっている人(A)に対して運動している人(B)の時間は遅れるんですよね? でも、Bから見たら、Bが止まっていてAが運動しているのだから、今度はAの時間が遅れることになっちゃいますよね? おかしくないですか?」
これは相対性理論に関して「よくある質問」の一つで、これに対する最も端的な回答は「おかしくないです」ということになります。このことについては、相対性理論に関する教科書的な本を見れば大体書いてありますし、これを複雑化させたのがいわゆる「双子のパラドックス」で、これも様々なところで解説されています。最近では、ヨビノリたくみさんによる秀逸な解説動画もあります:
この記事では「双子のパラドックス」には立ち入らず、互いに等速直線運動している関係の二つの慣性系での時間の進み方、そしてこのときに起きる「運動する人の時間の遅れ」について考えます。これには何通りかの説明の仕方がありますが、ここではローレンツ変換を使った説明をします。
まず、二つの慣性系 A, B を用意します。A に対して B が $${ x }$$ 軸の正の方向に速度 $${ V }$$ ($${ V > 0 }$$: 定数) で等速直線運動しているとき、A での 4次元座標 $${ (x_{\mathrm{A}}, y_{\mathrm{A}}, z_{\mathrm{A}}, c t_{\mathrm{A}}) }$$ と B での 4次元座標 $${ (x_{\mathrm{B}}, y_{\mathrm{B}}, z_{\mathrm{B}}, c t_{\mathrm{B}}) }$$ ($${ c }$$ は光速を表す) の間に
$$
x_{\mathrm{B}} = \gamma \left( x_{\mathrm{A}} - \frac{V}{c} \cdot c t_{\mathrm{A}} \right) ,
\quad y_{\mathrm{B}} = y_{\mathrm{A}} ,
\quad z_{\mathrm{B}} = z_{\mathrm{A}} ,
$$
$$
c t_{\mathrm{B}} = \gamma \left( c t_{\mathrm{A}} - \frac{V}{c} x_{\mathrm{A}} \right) ;
\qquad \gamma := \frac{1}{\sqrt{1 - \left( \frac{V}{c} \right)^2}}
$$
という関係が成り立ちます。これをローレンツ変換といいます。

$${ y }$$ 方向と $${ z }$$ 方向については省略して、以降
$$
x_{\mathrm{B}} = \gamma \left( x_{\mathrm{A}} - \frac{V}{c} \cdot c t_{\mathrm{A}} \right) ,
\quad c t_{\mathrm{B}} = \gamma \left( c t_{\mathrm{A}} - \frac{V}{c} x_{\mathrm{A}} \right) \qquad (\diamondsuit)
$$
およびその逆変換
$$
x_{\mathrm{A}} = \gamma \left( x_{\mathrm{B}} + \frac{V}{c} \cdot c t_{\mathrm{B}} \right) ,
\quad c t_{\mathrm{A}} = \gamma \left( c t_{\mathrm{B}} + \frac{V}{c} x_{\mathrm{B}} \right) \qquad (\clubsuit)
$$
を使っていきます。逆変換の式 $${ (\clubsuit) }$$ は、式 $${ (\diamondsuit) }$$ で速度 $${ V }$$ を $${ -V }$$ とすればよいですし、あるいは式 $${ (\diamondsuit) }$$ で $${ x_{\mathrm{A}} }$$ と $${ c t_{\mathrm{A}} }$$ を未知数として連立方程式を解く、と考えることでも導けます。これらを基にして、まず「運動する人の時間の遅れ」とはどういうことなのかを説明します。
「運動する人の時間の遅れ」とは
ある初期時刻 $${ t = 0 }$$ において、慣性系 A, B の原点が同じ位置にあり、B の原点 $${ x_{\mathrm{B}} =0 }$$ での時間の進み方を、A を基準として考えます。上の式 $${ (\diamondsuit) }$$ の第一式で $${ x_{\mathrm{B}} =0 }$$ とおくと
$$
x_{\mathrm{A}} = \frac{V}{c} \cdot c t_{\mathrm{A}}
$$
となり、これは B の原点が A の座標でどのように運動しているか($${ x }$$ 軸の方向に速度 $${ V }$$ で等速直線運動している)を表す式です。これを式 $${ (\diamondsuit) }$$ の第二式に代入すると
$$
c t_{\mathrm{B}} = \gamma \left( c t_{\mathrm{A}} - \left( \frac{V}{c} \right)^2 c t_{\mathrm{A}} \right)
= c t_{\mathrm{A}} \gamma \left( 1 - \left( \frac{V}{c} \right)^2 \right)
= c t_{\mathrm{A}} \sqrt{ 1 - \left( \frac{V}{c} \right)^2 }
$$
となって、$${ t_{\mathrm{B}} < t_{\mathrm{A}} }$$ であることが示されるので「B の方が A に比べて時間の進みが遅い」と言えます。あるいは、式 $${ (\clubsuit) }$$ の第二式で $${ x_{\mathrm{B}} =0 }$$ とおいて
$$
c t_{\mathrm{A}} = \gamma \cdot c t_{\mathrm{B}}
$$
となることからも同じ結果を得られます。
ここまでは慣性系 A を基準として、A に対して速度 $${ V }$$ で等速直線運動している慣性系 B での時間の進みが A に比べて遅れることを見てきたわけですが、では B を基準とするとどうなるでしょうか? 上と同じ設定で、ただし A の原点 $${ x_{\mathrm{A}} =0 }$$ での時間の進み方を考えることになりますが、上と同様の考察の結果
$$
c t_{\mathrm{A}} = \frac{1}{\gamma} \cdot c t_{\mathrm{B}}
= c t_{\mathrm{B}} \sqrt{ 1 - \left( \frac{V}{c} \right)^2 }
$$
ということが導かれ、今度は $${ t_{\mathrm{A}} < t_{\mathrm{B}} }$$ つまり「A の方が B に比べて時間の進みが遅い」ことが示されます。一見矛盾しているように見えますが、これは矛盾でも何でもなく、むしろ相対性理論がいかにうまくできているかを示している、とさえ言えます。そのことを以下で「時空図」を使って説明します。
時空図を使う
時空図とは、横軸に $${ x }$$ を、縦軸に $${ c t }$$ をとって時空での運動の様子を表すグラフのことです。二つの軸は通常直交させて書きますが、必ずしも直交させる必要はないです。ここでは、基準とする慣性系の方を直交させて書くことにします。

上の図は慣性系 A を基準として書いた時空図です。慣性系 B の $${ x }$$ 軸と $${ ct }$$ 軸は、ローレンツ変換の式 $${ (\diamondsuit) }$$ でそれぞれ $${ c t_{\mathrm{B}} = 0 }$$, $${ x_{\mathrm{B}} = 0 }$$ とおくことで得られ、それが図で紫で示した軸です。慣性系 A を直交座標系とすると、慣性系 B は斜交座標系となります。
先に述べた、A を基準としたときの A, B での時間の進みの関係 $${ c t_{\mathrm{B}} = \gamma^{-1} c t_{\mathrm{A}} }$$ を図の中に書き入れると、$${ T }$$ をある時間を表す定数として $${ c t_{\mathrm{A}} = c T }$$ のとき $${ c t_{\mathrm{B}} = \gamma^{-1} c T }$$ (図の黄色の星印)で、$${ c t_{\mathrm{B}} = c T }$$ のとき (図の緑の丸)には $${ c t_{\mathrm{A}} = \gamma c T }$$ ということになります。
赤の曲線は $${ (c t)^2 - x^2 = (c T)^2 }$$ という式で表される双曲線の一部です。ローレンツ変換では $${ (c t)^2 - x^2 }$$ が不変となるので、$${ x_{\mathrm{A}} = 0 }$$, $${ x_{\mathrm{B}} = 0 }$$ それぞれにおいて $${ c t_{\mathrm{A}} = c T }$$, $${ c t_{\mathrm{B}} = c T }$$ となることを示しています。
では、慣性系 B を基準として時空図を書くとどうなるでしょうか?

上の図3左は基準とする慣性系 B の $${ x }$$ 軸と $${ c t }$$ 軸が直交するように書いた時空図、図3右は慣性系 A を基準とした場合と比較がしやすいように、A の $${ x }$$ 軸と $${ c t }$$ 軸を直交させた状態で書いた時空図です。
A を基準としたときと同様にして A, B での時間の進みの関係 $${ c t_{\mathrm{A}} = \gamma^{-1} c t_{\mathrm{B}} }$$ を図の中に書き入れると、$${ T }$$ をある時間を表す定数として $${ c t_{\mathrm{B}} = c T }$$ のとき $${ c t_{\mathrm{A}} = \gamma^{-1} c T }$$ (図の赤の星印)で、$${ c t_{\mathrm{A}} = c T }$$ のとき (図の水色の丸)には $${ c t_{\mathrm{B}} = \gamma c T }$$ ということになります。注意してほしいのは、図3右において B を基準として A の時間の進みを見るときには、B の $${ \bm{x} }$$ 軸に平行な線を引いて A の $${ \bm{c t} }$$ 軸との交点を見なければならない、ということです。うっかり A の $${ x }$$ 軸に平行な線を引いて「あれ?おかしい。図2と同じになってしまう」とやってしまいがちですが、そうではないのです。A を基準とするか B を基準とするかで、この点が違います。このことは教科書等でよく「同時の相対性」と書かれています。
ここまでは、相対性理論に関する教科書や初歩的な解説をしている本などを見れば大体書いてあることです。本の場合はページの都合等で手短にしか書かれていないこともあるので、上の解説の方が少し詳しいかもしれません。
相対性理論の入門的な本は多数出版されていますが、私が知っている範囲で「時間の遅れ」について最も詳しく書いてある本は、恒岡美和著「明解 相対性理論入門 ー正しい理解を求めてー」聖文新社 です。具体的な計算例を使いながら、とても丁寧に書かれていて名著と言ってよい本と思いますが、出版社が廃業してしまったようで、現在入手可能なのは中古品のみのようです。
ローレンツ変換を基底の変換とみなす
前節までの内容は、少なくとも使っている数学のレベルとしては中学生・高校生でも理解できる内容ですが、この節では少しレベルを上げて、大学一年程度で学ぶ線形代数の知識を基にした解説をします。
まず、ローレンツ変換の式 $${ (\diamondsuit) }$$ および逆変換の式 $${ (\clubsuit) }$$ を、行列を使って
$$
\begin{pmatrix} x_{\mathrm{B}} \\ c t_{\mathrm{B}} \end{pmatrix}
= \Lambda \begin{pmatrix} x_{\mathrm{A}} \\ c t_{\mathrm{A}} \end{pmatrix} \ ;
\qquad \Lambda = \gamma \begin{pmatrix} 1 & - \dfrac{V}{c} \\ - \dfrac{V}{c} & 1 \end{pmatrix} \qquad (\diamondsuit')
$$
$$
\begin{pmatrix} x_{\mathrm{A}} \\ c t_{\mathrm{A}} \end{pmatrix}
= \Lambda^{-1} \begin{pmatrix} x_{\mathrm{B}} \\ c t_{\mathrm{B}} \end{pmatrix} \ ;
\qquad \Lambda^{-1} = \gamma \begin{pmatrix} 1 & \dfrac{V}{c} \\ \dfrac{V}{c} & 1 \end{pmatrix} \qquad (\clubsuit')
$$
と書きます。この行列 $${ \Lambda }$$ はローレンツ変換を表す行列です。このように、ローレンツ変換を一次変換と見なすことにより「時間の遅れ」の数学的な意味を考えていきます。
ここで、前の記事「一次変換と座標変換の悩ましい関係」でも述べた基底を考えます。大事なポイントなので今一度書くと、基底とは、高校数学で学ぶ「平面ベクトル」のところで出てくる基本ベクトル
$$
\bm{e}_x = \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \quad
\bm{e}_y = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
$$
の一般化です。基本ベクトルを使えば平面上のどんなベクトルでも、その線形結合で表すことができますが、基本ベクトルでなくても一次独立な二つのベクトルで同様のことができます。このように、平面や空間の任意のベクトルを線形結合で表すために必要な、一次独立なベクトルの集合を基底といいます。特に基本ベクトルの集合 $${ E = \left\{ \bm{e}_x , \bm{e}_y \right\} }$$ を標準基底といいます。そして、ある平面ベクトル $${ \bm{V} }$$ を $${ \bm{V} = V_x \bm{e}_x + V_y \bm{e}_y }$$ と表したとき、$${ V_x , V_y }$$ を通常 $${ \bm{V} }$$ の成分といいますが、別の基底 $${ F = \left \{ \bm{f}_1 , \bm{f}_2 \right \} }$$ をとって $${ \bm{V} = v_1 \bm{f}_1 + v_2 \bm{f}_2 }$$ と表すこともできるわけで、この場合は $${ v_1 , v_2 }$$ が $${ \bm{V} }$$ の基底 $${ F }$$ に関する成分、ということになります。基底の取り方は無数にあり、ベクトルの成分というのは基底の取り方によって変わります。そして基底の取り方というのは座標系の取り方ということであり、座標変換とは基底の変換です。

以上を踏まえて、慣性系 A, B に対して、それぞれの $${ x }$$ 軸方向と $${ c t }$$ 軸方向を向く単位ベクトルにより基底を定め、それを A については $${ \left\{ \bm{a}_1 , \bm{a}_2 \right\} }$$ とし Bについては $${ \left\{ \bm{b}_1 , \bm{b}_2 \right\} }$$ とします。時空内のあるベクトル $${ \bm{x} }$$ が慣性系 A では $${ (x_{\mathrm{A}}, c t_{\mathrm{A}}) }$$ を成分として持ち、慣性系 B では $${ (x_{\mathrm{B}}, c t_{\mathrm{B}}) }$$ を成分として持つとき、このベクトル $${ \bm{x} }$$ は
$$
\bm{x} = x_{\mathrm{A}} \bm{a}_1 + c t_{\mathrm{A}} \bm{a}_2
= x_{\mathrm{B}} \bm{b}_1 + c t_{\mathrm{B}} \bm{b}_2
$$
と二通りの線形結合で表されますが、このとき基底はそれぞれの系での「単位長さ」や「単位時間」を与え、成分はその「単位長さ」や「単位時間」の下での長さ・時間を表すわけです。そして、慣性系 A, B 間での成分同士の変換則を与えるのが式 $${ (\diamondsuit') }$$ あるいは $${ (\clubsuit') }$$ です。前の記事で述べた通り、基底の変換則とベクトルの成分の変換則は互いに逆変換の関係になりますので、基底は
$$
\bm{b}_1 = \Lambda^{-1} \bm{a}_1 \ , \quad \bm{b}_2 = \Lambda^{-1} \bm{a}_2
$$
と変換されます。基底 $${ \left\{ \bm{a}_1 , \bm{a}_2 \right\} }$$ を標準基底のようにとって
$$
\bm{a}_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \quad
\bm{a}_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
$$
とすると
$$
\bm{b}_1 = \gamma \begin{pmatrix} 1 \\ \frac{V}{c} \end{pmatrix}
= \gamma \left( \bm{a}_1 + \frac{V}{c} \bm{a}_2 \right) , \quad
\bm{b}_2 = \gamma \begin{pmatrix} \frac{V}{c} \\ 1 \end{pmatrix}
= \gamma \left( \frac{V}{c} \bm{a}_1 + \bm{a}_2 \right)
$$
となり、$${ \bm{b}_1 , \bm{b}_2 }$$ を $${ \bm{a}_1 , \bm{a}_2 }$$ の線形結合で表せます。逆に $${ \bm{a}_1 , \bm{a}_2 }$$ を $${ \bm{b}_1 , \bm{b}_2 }$$ の線形結合で表すと
$$
\bm{a}_1 = \gamma \left( \bm{b}_1 - \frac{V}{c} \bm{b}_2 \right) , \quad
\bm{a}_2 = \gamma \left( - \frac{V}{c} \bm{b}_1 + \bm{b}_2 \right)
$$
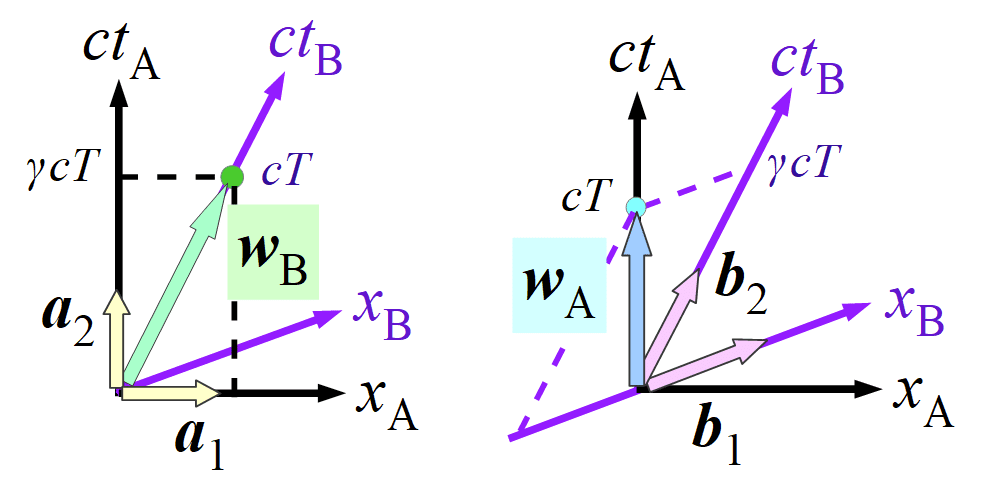
となります。ここで、慣性系 A, B それぞれにおいて時間 $${ T }$$ の間、静止していることを表すベクトル $${ \bm{w}_{\mathrm{A}} , \bm{w}_{\mathrm{B}} }$$ を考えると、それらは上の基底を使って
$$
\bm{w}_{\mathrm{A}} = c T \bm{a}_2 \ , \qquad \bm{w}_{\mathrm{B}} = c T \bm{b}_2
$$
と表せます。前々節で行った「慣性系 A を基準として、B での時間の進み方を見る」ということは、「ベクトル $${ \bm{w}_{\mathrm{B}} }$$ を A の基底 $${ \left\{ \bm{a}_1 , \bm{a}_2 \right\} }$$ で表して、その $${ \bm{a}_2 }$$ に掛かっている係数を見る」ということに対応します。実際にやってみると
$$
\bm{w}_{\mathrm{B}} = \gamma c T \left( \frac{V}{c} \bm{a}_1 + \bm{a}_2 \right)
$$
となって、慣性系 A を基準とすると B で時間 $${ T }$$ が経過する間に A では $${ \gamma T }$$ が経過していることが示されます。つまり「基準に対して等速直線運動している系の時間の進みと比べて、基準とする系の時間は $${ \gamma }$$ 倍早く進む」ということが分かります。「慣性系 B を基準として、A での時間の進み方を見る」という方も同様にやってみると
$$
\bm{w}_{\mathrm{A}} = \gamma c T \left( - \frac{V}{c} \bm{b}_1 + \bm{b}_2 \right)
$$
となって、こちらもやはり同様の結論が得られます。これらの様子を図で表すと、以下の通りです:
ここでやっていることは本質的に前々節でやったことと同じで、基底や一次変換といった線形代数で出てくる考え方を前面に出すかどうかだけの違いです。前々節でのやり方の方が使う数学は初歩的なもので済みますが、その意味を正しく理解するのは時空図を書くなど図示してみないと難しいところがあるのではないかと思います。特に「時間の遅れ」とか「同時の相対性」といった時間に関わることは、我々の日常の感覚と大きく異なるため、誤解されやすいです。もし線形代数の知識がある程度あるのであれば、この節で示した見方は「時間の遅れ」という一般にはかなり非自明に思えることを、機械的な数学の問題としてとらえることができる点で有意義ではないかと思います。
高校から大学の初年度にかけて学ぶ数学の中で、微積分は様々な場面で使われるため、その重要性が認識されやすい一方、線形代数はその重要性がよく分からないと言われることが多いです。しかし、線形代数は時に物理理論の数学的な枠組みを与えてくれて、理論の深い理解には不可欠であると言えます。上述した「時間の遅れ」に関することは、そのごく小さな一例ではありますが、この記事が線形代数を学ぶ動議づけの一助となれば幸いです。
