
「文字式」って何ですか?
こんにちは。ここでは身近に感じやすい理数(数学や物理)・言語(英語)系の記事を書いていこうと思っています。数学系の第1回目は数学の「文字式」について書いてみます。
文字式については、その名の通り、文字を使った式です。例えば「2a+b」や「3x」みたいなものです。しかし、この書き方自体、それまで習ってきた数字だけの「数学」からは解離も大きく、中には「なんで数学なのに文字を使うんだ!」と考えて混乱してしまい、そのまま数学が苦手になってしまった人もいるかもしれません。ここでは数学の歴史と共に文字式の意味について考えていきます。
文字式は方程式を解くために生まれた
そもそも文字式はどうして作られたのでしょうか。私たちが文字式を習う前にはその概念がなかったように、古代の人たちにとってもそれは同じでした。文字が生まれる前の数学は多くが幾何学に関連して記述されました。
たとえば、これは古代バビロニアの記録で、正方形の一辺の長さを求める問題です。
「正方形の面積から、一辺の長さの4倍が引かれて780」
文字で書くと、正方形の一辺をXとすれば、正方形の面積は「X²」で、一辺の長さの4倍は「4X」ですから、「X²-4X=780」を意味しています。
しかし、この当時はまだ「文字式」がないので、現代の私たちのようには記載することができませんでした。当時の人たちは文字式を使わずに「言葉」だけを用いて方程式を解いていたのです。
紀元3世紀ごろのギリシャの数学者ディオファントスが、世界で初めて文字式を発明します。ディオファントスの方式に従うと、上記の文字式は以下のように書くことができます。
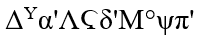
現代の文字式とは異なり一つの変数しか扱うことができませんし、そもそもかなり読みにくいですが、それでもそれ以前には文字式がなかったことを考えると、ディオファントスの方法は画期的でした。しかし、その後ディオファントスの代数記号を継承した数学者もおらず、この方法は廃れてしまいます。
文字式がない間も数学の研究は続いていました。例えば、9世紀のアラビアの数学者アル・フワーリズミ(Al-kwarizmi、彼の名前は「アルゴリズム」という言葉の語源にもなっている)は二次方程式の解法を一般的に解く方法を発見しています。
しかし、フワーリズミの方法は、「X²」を「マール」、「X」を「シャイ」、定数項を「数」としたときに、二次方程式を6種類に分ける必要がありました。具体的には以下の通りです。
①マールがシャイに等しい
②マールが数に等しい
③シャイが数に等しい
④マールとシャイの和が数に等しい
⑤マールと数の和がシャイに等しい
⑥マールがシャイと数の和に等しい
上記の「X²-4X-780=0」をフワーリズミの言葉で書くのであれば「マール1個は、シャイ4個と780の和に等しい」と書かれることになります。したがって上記の⑥の方法で計算されることになります。
フワーリズミの解法はそれぞれを図形的に考えて解く方法でしたが、どのような場合の二次方程式でも解くことができました。この解法は具体的な数字を考えずとも図形を用いて一般化されていることから、「文字の代わり」、すなわち「代数」的な解法であると言えます。フワーリズミは古典的な意味での「代数学」の始まりであるとされることが多いです。(※誤解を招く表現ですが、現代の「代数学」はこの意味での「代数」とは別の学問です)
しかし、現代の二次方程式の解の公式と比べると、場合分けも多く、とても難解な解法をとっています。
現代につながる文字式の発明
時代は下り、中世暗黒時代を終えてルネサンスの時代に入ると、ヨーロッパではアラビアを経由して保存されてきた古代ギリシャの書物が再輸入され、そこで再び数学の研究が再開されます。二次方程式を一般に解く方法こそ解明されましたが、何行にも分けて言葉で記述される時期が続きました。
様々な数学者が時代を掛けて記号法を各々に編み出していきましたが、1591年にフランソワ・ヴィエト(François Viète)が未知数を母音A,E,I,O,Uで表し、既知数を子音B,C,D等によって表す方法を発表したことで複数の文字を扱う方法が確立され、最終的にデカルトが現在のように未知数をX,Y,Zで表し、既知数をA,B,C等によって表す方法を確立させて現代に至ります。
文字式を用いることで、二次方程式の解はたった一行の式で記載されることになります。
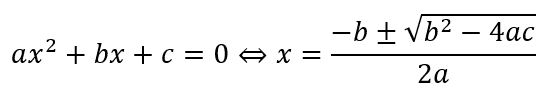
まとめ
まとめると次のようになります。文字式が生まれる遥かに前から古代の人々は方程式を一般的に解く方法を編み出してきましたが、その方法は「言葉」によるものでした。時代が下り、「文字式」が発明されることで、難解な「言葉」を用いずとも、たった一行の式で方程式を解くことができるようになりました。
余談になりますが、鎖国下にあった江戸時代の日本では、世界に類を見ない「和算」のブームが起こりましたが、この和算ブームを支えたのは、関孝和が考案した「傍書法」と「点竄術(てんざんじゅつ)」でした。「傍書法」とは算木における記数法と甲乙丙などの文字を用いた文字式のことで、文字式を取り入れることでそれまで解けなかった数々の難問を解くことができるようになり、和算は西洋数学に劣らない先進性を手に入れ発展していったのです。
文字式は数学を難解にさせるものではなく、数学を易しく解くための工夫だったのです。文字式を使わずに方程式を解いていた時代を考えれば、現代の私たちが学ぶのが文字式でよかったと思えるかもしれませんね。(記事終わり)
