
文系人間、数学的帰納法をあみだくじから学ぶ
あみだくじ、といえば、Marmalade!
と思ってくださる方も何人かいらっしゃるかもと思います。
今日はそんな私が、あみだくじについて
最近学んだことを書いてみます♪
あみだくじって不思議ですよね。
単純な作りなのに、
必ず、きちんと組み合わせになるんです。
それがどうしてか知っている?
と知人からきかれて、
知らないから教えてください♪と
飛びついたところから始まります。
ところで自他ともに認める
文系人間な私ですから、
自己流解釈になっておりますので
あしからずお読みくださいませ。
〇
話は「数学的帰納法って知っている?」
から始まりました。
数学的帰納法、知っているわけない!(笑)
数学的帰納法とは
「自然数nに関する命題Pが、すべての自然数について成り立つ」
ということを
①n=1のときに命題Pが成り立つことを証明する
②n=kで命題Pが成り立つと仮定すると、n=k+1でも命題Pが成り立つことを証明する
なのですが、彼はこう説明しました。
あのね、n(これ)が成り立って
さらに、これ+1が成り立ったら
ふたつがなりたつでしょ?
そのように2個成り立てば
いくら増やしても成り立つって言う法則
え?どういうこと?
全く良くわからなかった私。
ひとつのことがなりたつ
さらに、それに+1したことがなりたつ
そうすると、2つのことが成り立ってことになる。
そうするといくら増やしてもこのことは
成り立つっていうのが数学的帰納法っていうの
???なんとなくわかったかな?
わからないような気もするし
わかったような気もする。
とりあえず、なんとなくでもいいから
覚えるように言われました。
これをあみだくじに当てはめます。
ここからは図解しますよ。
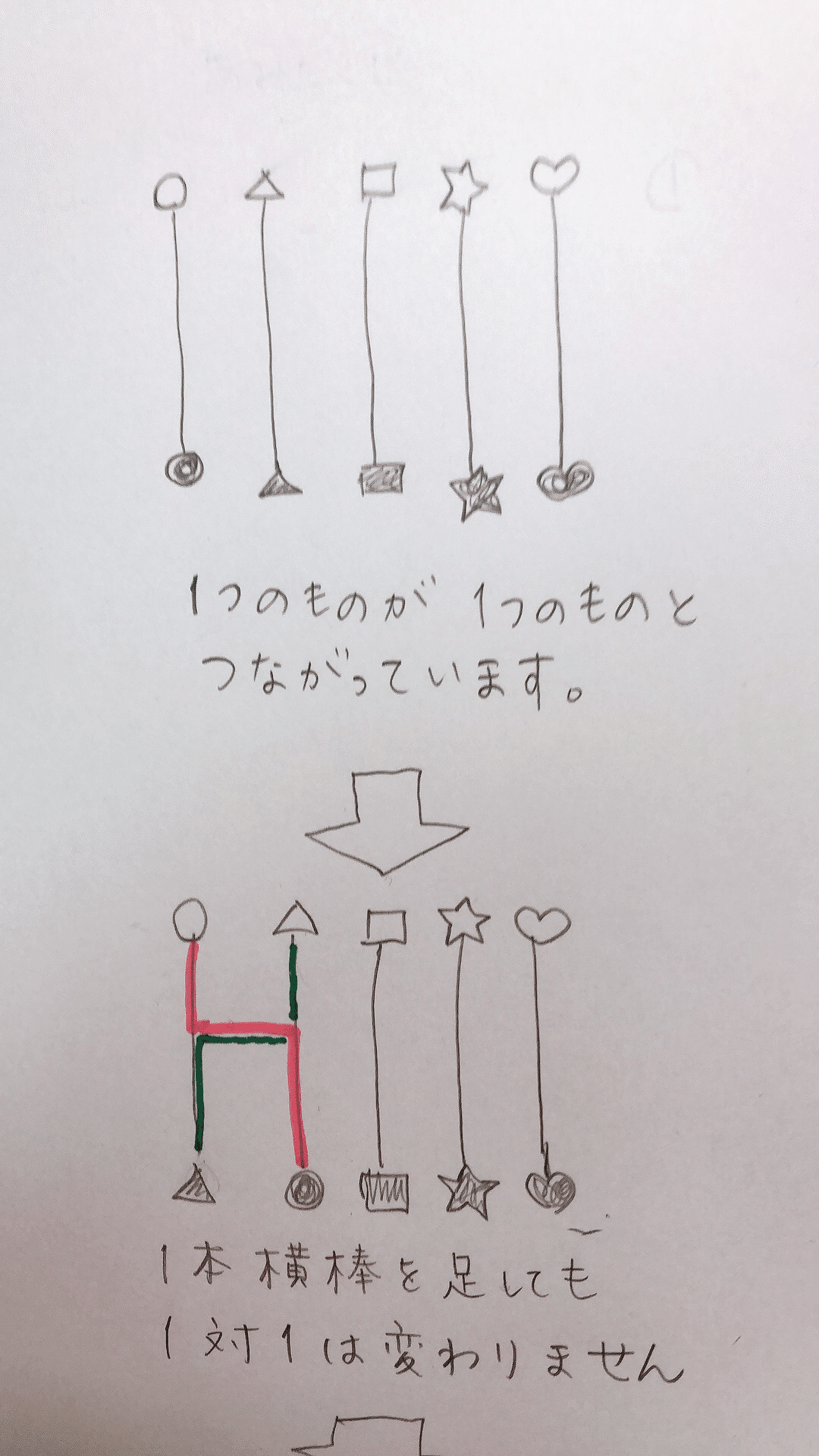
ということがなりたっています

これもちゃんと1対1になります。
このことで、横棒を1本足しても
2本足しても、上と下が1:1で
つながることがわかります。
数学的帰納法を当てはめると、
2つのことが証明されたので、
この横棒は何本増やしても大丈夫だという
数学的帰納法が当てはまることになります。
だから百本の横棒を引こうとも
かならず、上と下は1:1でつながることになる
っという話でした。
こちら、わたしなりの解釈になるので
本当かどうかわかりません(笑)(笑)
ちなみにあみだくじの由来は
阿弥陀如来像が後ろにしょっている後光?の
飾りからきたようです。
というわけで、
最近ちょっとだけ賢くなったような気がする
というお話でした♪
みなさま良い日曜日の夜をおすごしくださいね。
