
レンズとボケについての誤解を解く
こんにちは、きたと申します
最近、写真家の塙さんがこのようなツイートをされて、一部界隈で議論となりました

この話題を期に、レンズについて調べたくなった方も少なくないでしょう
フルサイズ50mmとAPS-Cの33mmのレンズで何が違うのか?
フルサイズの方がボケるのは当たり前だろう
というわけで今回は
カメラに使い慣れている人でもあまりきちんと理解されていないレンズとボケの関係を書いていこうと思います。
調べると出てくる許容錯乱円という言葉
レンズについて調べると聞き慣れない言葉が出てきます
その中でもボケや被写界深度と深い関わりのある「許容錯乱円」という言葉
おそらく多くの人がこの言葉に惑わされて理解に苦しむでしょう
この記事ではなるべく許容錯乱円は使わずに、レンズとボケの関係を説明していきます
最後の補足で、許容錯乱円について足がかりとなる話は書きます
言葉の確認
世間では「ボケ量」や「良くボケる」など、ボケの何を語っているのか分からない場合や、個人の感覚で書かれがちですが
ここでは理解を進めるためにボケの大きさと深さという言葉を使って説明していきます

・ボケの大きさ=玉ボケの大きさ
・ボケの深さ=被写界深度の深さ(ピント面の深さ)
このことを頭に入れて先に進みます
同じ焦点距離F値のレンズを使って、センサーサイズを変えた場合

知っている人にとっては当たり前だろうというところから始めます
青色で囲った外側の円はレンズを覗き込んだ穴だと考えて下さい。
この円がレンズに写る最大範囲で、イメージサークルと言います
ここから、3:2の長方形をどれくらいの大きさで切り出すか
というのがセンサーサイズを選ぶことになります。
サイズの大きいフルサイズでは円の外側まできっちり使え
サイズの小さいAPS-Cでは、さらにその内側のいち部分だけを切り出します。
APS-Cの方が狭い範囲で撮影しているので、より望遠に写るのはそのためですよね
ここから一般的に誤解を受けていることを説明していきます
何度も言いますが
レンズによって見えている絵をどの範囲で切り出すかの違いです。
↑これ、とても当たり前のことを言っていますがとても重要です

上の図は先程の白樺の写真を
フルサイズとAPS-Cで変えたときに起こる変化を示します。
ここで注目してほしいのは
センサーサイズとともに変化するのは画角です!
被写界深度は変わっていません!

フルサイズになったからと言ってボケの深さに変化はないということです。
同じことの言い換えですが、被写界深度はレンズの設定で決まり、センサーサイズによっては変わっていません。

ではボケの大きさはどうなるかというと
APS-Cのほうが大きくなります
ボケの大きさというのが画面内の直径の比率を指標にしているからです

より簡単に言うと、一部分を切り出したAPS-Cは1.5倍することでフルサイズの縦横幅に合わせるので、玉ボケも1.5倍大きくなります
では次に
ボケの深さが焦点距離とF値でどう変化するのか説明していきます
焦点距離とF値 vs 被写界深度

さて突然ですが問題です
・50mm f1.8
・33mm f1.4
・80mm f2.8
この3つの中で一番ボケが深く(被写界深度が狭く)なるのはどれでしょうか?
何度も言いますが、被写界深度はセンサーサイズで変わりません
焦点距離やF値で大きく変わります
正解は、、、
80mm f2.8
です

どうやって導くかですが焦点距離の2乗をf値で割った数というのが、およそ被写界深度に反比例します
つまり
焦点距離×焦点距離÷f値の数値が大きいほど、ボケが深く(被写界深度が狭く)なると覚えて下さい
※補足でもう少しきちんと説明します
注意として
焦点距離×焦点距離÷f値の数値だけでは、正確な被写界深度は求められません。あくまで簡単な比較方法です。
また、マクロ撮影の場合はこれに沿わないので、使えません。
ちなみにこの焦点距離÷f値の数値が大きいほどボケの大きさが大きくなります。

では一般的に議論される
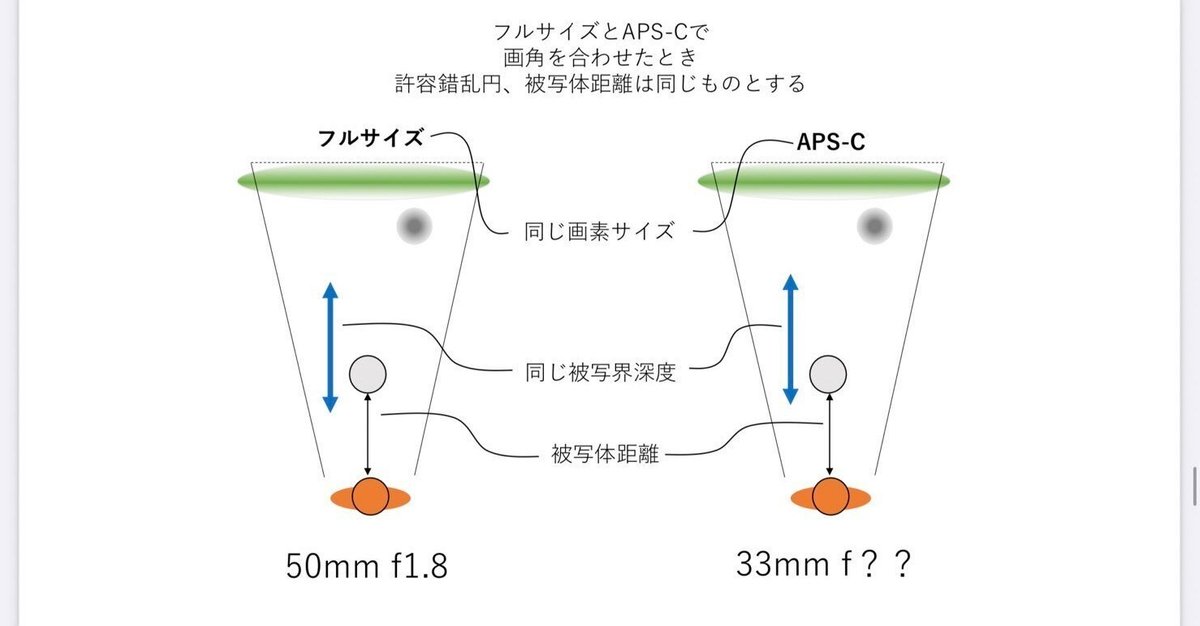
フルサイズとAPS-Cで画角を合わせた場合ではどうなるのか見てみましょう

先程の比較方法を使って
フルサイズのほうが、焦点距離の長いレンズを使うことになるので、よりボケが大きく、深くなることがわかります。
まとめ

曲解はありますが以上のように覚えておけば、少し写真とレンズの関係がわかってくれたと思います
皆様の理解の助けになれたでしょうか?
ここから先はもう少し知りたい方や内容の補足をしていきます
補足1:許容錯乱円をちょっとわかるようになる
まずはレンズに入った光がイメージセンサー付近で集光されたイメージして下さい
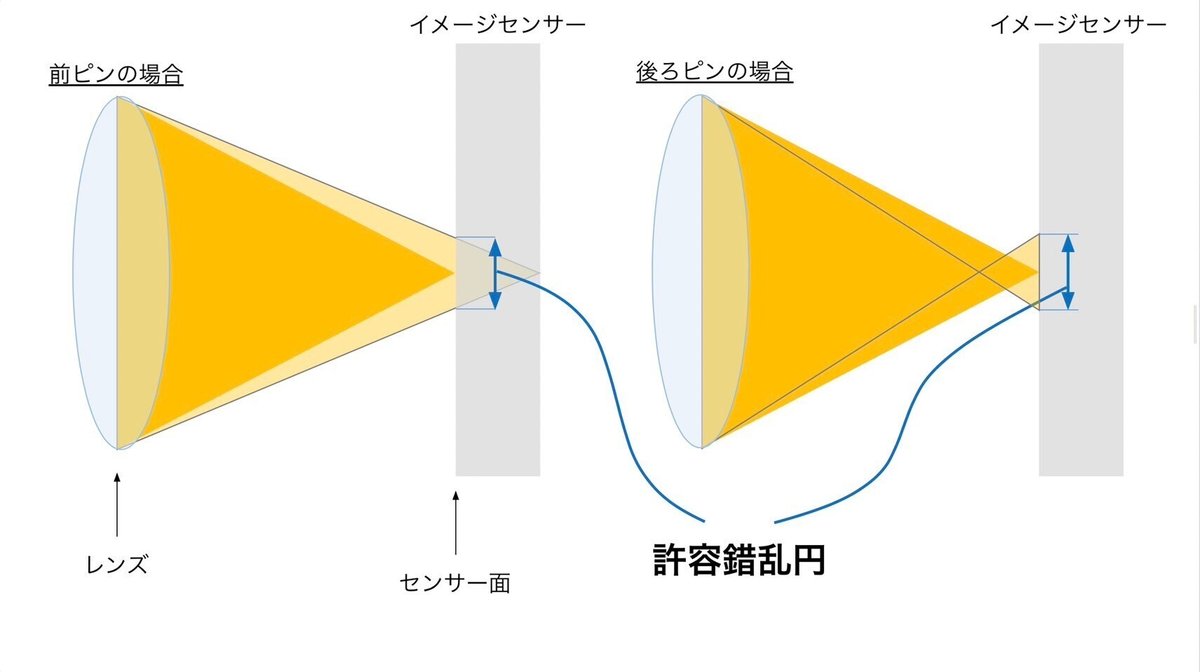
濃い黄色はセンサー面で最も集光された場合で薄い黄色は前ピンや後ろピンの場合の光です
現実のレンズでもどんなに集光しても点にはならず、必ず円になります。
この集光しきれていないこの円のことを「許容錯乱円」と言います。
また少し意味は違うが「エアリーディスク径」と書かれることもあります。
では、この許容錯乱円がボケとどのように関わってくるか考えてみましょう
まずピントがあっている状態(集光されている状態)とは
光が他の画素に漏れないで、1つの画素に収まる状態のことを指します。

上の図は画素数で比較した場合を描いています。
例えば、左の低画素センサーに少しボケた状態で光が集光されたとします。
その場合、例えボケて許容錯乱円広がっていても、1画素に収まっていればピントがあっていると見なせます
対して右の高画素の場合、同じくボケた光が入ってきて許容錯乱円が広がっている場合、別の画素に光が漏れてしまうため、ボケた光かピントがあった光かを区別することができます。
簡単な実験としてボケた写真の画素数を下げた写真と比べてみました

右はしっかりボケているとわかりますが
左は判別が付かなくなっているように見えますよね
このように、レンズだけでなく
センサーの画素の大きさがボケに関わってきます。
続けて、他にボケているかどうかを分ける場合が他にもあります。それは人が写真を鑑賞するときの人の視力の問題です

とても当たり前のことですが
観賞するときの写真との距離が近ければ、細かいところまではっきり見えます。
言い換えると、近くで見るほど、ボケているかどうか判別ができるということです。
広告など大きい写真の場合、全体像を見るには下がって見る必要があるため、多少荒いドットでも解像しているように見えます。
つまり、大きい写真を鑑賞する場合は許容錯乱円は大きくても問題になりません。

では、最後に簡単にまとめます。
許容錯乱円はどこの場面を想定して許容とするかによって値を自由に決めれます。
例えば、PCディスプレイのドットの等倍で毎回確認する場合は、カメラの画素ピッチ1〜2倍を設定します。
許容錯乱円少し馴染みが深くなりましたでしょうか?
具体的な被写界深度を計算する場合、許容錯乱円を扱う必要があるため、覚えておいて損はないはずです
補足2:被写界深度の簡単な比較方法
焦点距離×焦点距離/F値を指標にして比較するとそのまま被写界深度の比較になると説明しました。なぜそうなるのか詳しく話をしていきます
ちなみに
焦点距離/F値は有効口径という名称があり
F値の方が使い勝手がいいので良く使われる言葉ですが、本来は焦点距離/有効口径で導かれる値がF値です。(レンズの要素を理解する順序が逆)
話が脱線しましたが
この筑波大の方のページに被写界深度を導く数式が乗っています
この最後の式が被写界深度を導く式

これを有効口径Dで変換し計算します

有効口径×焦点距離におよそ反比例する形になりました。
これをグラフで確認してみます

焦点距離×有効口径が大きくなるほど、被写界深度が浅くなっていくのがわかります
正確ではありませんが
被写界深度をあるレンズで揃えたい場合
焦点距離×有効口径の値が同じになればおよそ近い被写界深度のレンズになります。
例えば、50mmと33mmを比較します
50mm f1.8は焦点距離×有効口径1389
33mm の焦点距離×有効口径1389になるには
f0.8必要です
被写界深度を計算すると(被写体までの距離1mや許容錯乱円0.03mmで同じとする)
50mmf1.8 : 43mm
33mmf0.8 : 44mm
もし興味があれば検算してみて下さい
最後まで読んで頂きありがとうございました。
