「1+2+3+…=-1/12」及び「1+2+3+…=∞」の同時の視覚化

直感的には、$${1+2+3+…}$$は$${∞}$$である。しかし、ある種の数学的な手法を使用すると、$${1+2+3+…=- \frac{1}{12}}$$が成立するらしい。

以下では、筆者は下記の数式を使用して、$${1+2+3+…=- \frac{1}{12}}$$を直感的に視覚化した。その時、彼はMacのアプリケーションソフトウェア「Grapher（グラファー）」で視覚化した。

$$
\sum_{k=1}^{∞}kexp(-kx)cos(kx)
$$

彼は上記の数式を杉山式と便宜的に呼ぶ。その式は杉山の「この電子場所」に依存する。

1章　結論

筆者は上記の杉山式を使用して、上記の2種類の現象を同時に視覚化した。なお、極限に関する数式も杉山の「この電子場所」に依存する。

$$
\lim_{x  \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)=-\frac{1}{12}
$$

$$
\sum_{k=1}^{∞}kexp(-k \cdot0)cos(k\cdot0)=∞
$$

上の数式では、$${k}$$を大きくすると、$${-\frac{1}{12}}$$が$${x>0}$$から$${x=0}$$へと近づいていく視覚化が得られた。つまり、上の数式では、$${1+2+3+…}$$が$${- \frac{1}{12}}$$になった。

下の数式では、$${k}$$を大きくすると、$${x=0}$$における値が$${1+2+3+…}$$ のように、無限に近づいてく視覚化が得られた。$${k}$$を大きくすると、$${x=0}$$における値は$${1}$$、$${1+2}$$、$${1+2+3}$$、…のようになった。つまり、下の数式では、$${1+2+3+…}$$が$${∞}$$になった。

2章　視覚化

以下では、筆者は$${1+2+3+…=∞}$$と$${1+2+3+…=- \frac{1}{12}}$$を同時に視覚化した。

1節 k=1の場合

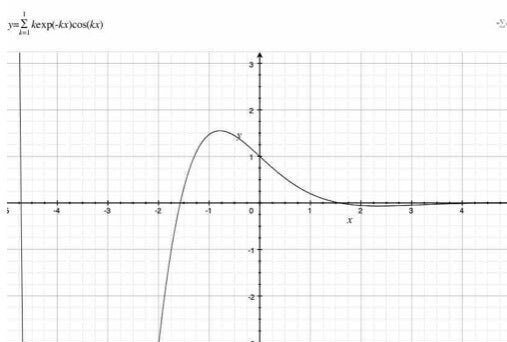
$$
\sum_{k=1}^{1}kexp(-k \cdot x)cos(k\cdot x)
$$

上記の図1を見ると、$${x=0}$$における値は$${1}$$になっている。杉山式で計算すると、次になる。

$$
\sum_{k=1}^{1}kexp(-k \cdot 0)cos(k\cdot 0)=1exp(-1 \cdot 0)cos(1\cdot 0)=1
$$

なお、$${exp(0)cos(0)＝1}$$である。この$${x=0}$$における$${1}$$が$${1+2+3+\dots}$$における1項目の$${1}$$に対応する。

2節 k=2の場合

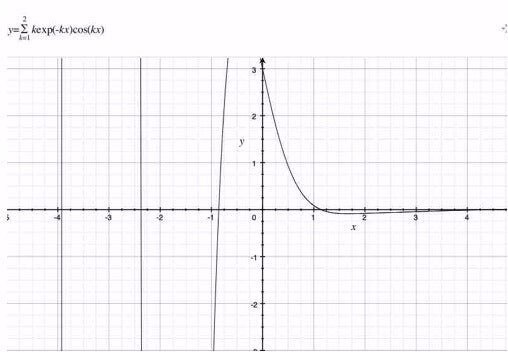
$$
\sum_{k=1}^{2}kexp(-k \cdot x)cos(k\cdot x)
$$

上記の図2を見ると、$${x=0}$$における値は$${3}$$になっている。杉山式で計算すると、次になる。

$$
\sum_{k=1}^{2}kexp(-k \cdot 0)cos(k\cdot 0)=1exp(-1 \cdot 0)cos(1\cdot 0)+2exp(-2 \cdot 0)cos(2\cdot 0)=1+2=3
$$

上記の数式は長いので、横に滑らせて（スライドさせて）、右端の数式を見ることができる。この$${x=0}$$における$${3}$$が$${1+2+3+\dots}$$における1項目の$${1}$$と2項目の$${2}$$の和に対応する。

3節 k=10の場合

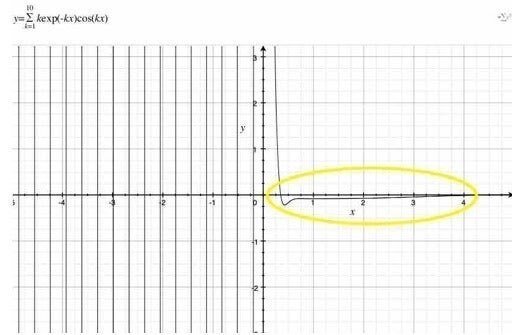
$$
\sum_{k=1}^{10}kexp(-k \cdot x)cos(k\cdot x)
$$

上記の図3を見ると、$${x=0}$$における値は見えない。杉山式で計算すると、次になる。

$$
\sum_{k=1}^{10}kexp(-k \cdot 0)cos(k\cdot 0)=1exp(-1 \cdot 0)cos(1\cdot 0)+2exp(-2 \cdot 0)cos(2\cdot 0)+\dots+10exp(-10 \cdot 0)cos(10\cdot 0)=1+2+\dots+10=55
$$

上記の数式は長いので、横に滑らせて（スライドさせて）、右端の数式を見ることができる。この$${x=0}$$における$${55}$$が$${1+2+3+\dots}$$における1項目の$${1}$$から10項目の$${10}$$までの和に対応する。

上記の黄色い楕円で囲まれた部分がある。その部分には、ある特定の値が存在しているように見える。$${k}$$を大きくすると、この値が$${- \frac{1}{12}}$$になる。

4節 k=100の場合

図4

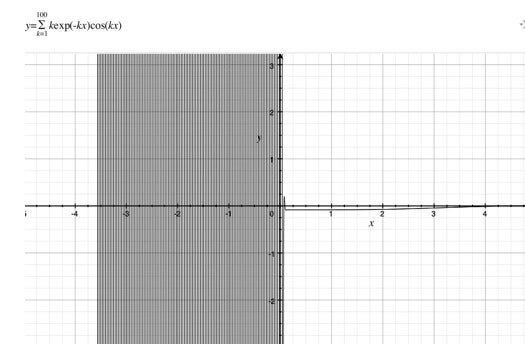
$$
\sum_{k=1}^{100}kexp(-k \cdot x)cos(k\cdot x)
$$

上記の図4を見ると、$${x=0}$$における値は見えない。杉山式で計算すると、次になる。

$$
\sum_{k=1}^{100}kexp(-k \cdot 0)cos(k\cdot 0)=1exp(-1 \cdot 0)cos(1\cdot 0)+2exp(-2 \cdot 0)cos(2\cdot 0)+\dots+100exp(-100 \cdot 0)cos(100\cdot 0)=1+2+\dots+100=5050
$$

上記の数式は非常に長いので、横に滑らせて（スライドさせて）、右端の数式を見ることができる。この$${x=0}$$における$${5050}$$が$${1+2+3+\dots}$$における1項目の$${1}$$から100項目の$${100}$$までの和に対応する。

上記の図4を見ると、$${x>0}$$では、特定の値が存在しているように見える。そこで、筆者は上記の図4を拡大してみる。

図5

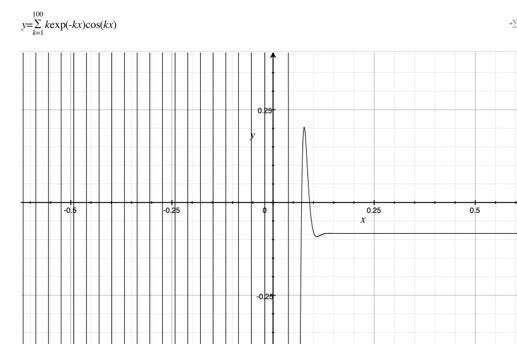
図5では、特定の値は$${- \frac{1}{12}}$$であるように見える。そこで、筆者は$${y=- \frac{1}{12}}$$を導入する。

図6

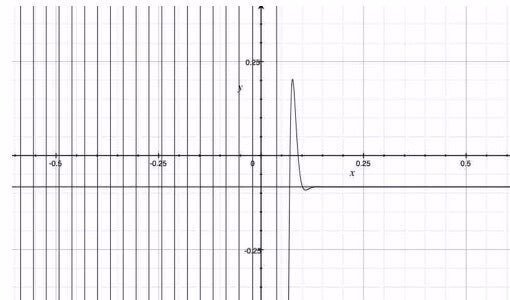
$${y=- \frac{1}{12}}$$と$${x>0}$$における特定の値が一致している。もし$${k}$$を無限に大きくするならば、$${x>0}$$における特定の値$${- \frac{1}{12}}$$もより$${x=0}$$に近づいていくように思える。

5節 k=∞の場合

$$
\sum_{k=1}^{∞}kexp(-k \cdot x)cos(k\cdot x)
$$

$${x=0}$$における値は当然見えない。$${x=0}$$における値を杉山式で計算すると、次になる。

$$
\sum_{k=1}^{∞}kexp(-k \cdot 0)cos(k\cdot 0)=1exp(-1 \cdot 0)cos(1\cdot 0)+2exp(-2 \cdot 0)cos(2\cdot 0)+\dots =1+2+\dots=∞
$$

上記の数式は長いので、横に滑らせて（スライドさせて）、右端の数式を見ることができる。この$${x=0}$$における$${∞}$$が$${1+2+3+\dots}$$における1項目の$${1}$$から∞項目の$${∞}$$までの和に対応する。

この時、上記の結論で提示されたように、次の式が成立する。

$$
\sum_{k=1}^{∞}kexp(-k \cdot0)cos(k\cdot0)=∞
$$

同時に、もし筆者が$${0}$$を杉山式に代入せずに、$${x}$$を$${x>0}$$から$${x=0}$$に近づけていくならば、その時、杉山式の$${x=0}$$における極限値（収束値？）は$${- \frac{1}{12}}$$になるように思える。

この時、上記の結論で提示されたように、次の式が成立する。

$$
\lim_{x  \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)=-\frac{1}{12}
$$

3章　解釈

以下では、筆者は上記を簡単に解釈する。

$$
\sum_{k=1}^{∞}kexp(-kx)cos(kx)
$$

彼は上記の数式を使用して、解釈する。

1節　1+2+3+…=∞

$$
\sum_{k=1}^{∞}kexp(-k \cdot0)cos(k\cdot0)=∞
$$

$${1+2+3+\dots}$$は$${∞}$$である。感覚的には、これは正しい。

杉山式では、$${1+2+3+\dots=∞}$$は$${\sum_{k=1}^{∞}kexp(-k \cdot x)cos(k\cdot x)}$$における$${x=0}$$での値である。視覚的には、$${x=0}$$において、$${1+2+3+\dots}$$が生じる。

2節　1+2+3+…=-1/12

$$
\lim_{x  \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)=-\frac{1}{12}
$$

ある種の手法を使用すると、$${1+2+3+\dots}$$は$${- \frac{1}{12}}$$になる。これは直感に反する。

杉山式では、$${1+2+3+…=- \frac{1}{12}}$$は$${\sum_{k=1}^{∞}kexp(-k \cdot x)cos(k\cdot x)}$$における$${x>0}$$から$${x=0}$$への極限の値である。

参考

（1） 自然数の総和がゼータ関数の-1/12であることの新しい証明

筆者は上記の数式を上記の電子場所から引用した。

動画（youtube）

上記の動画は上記の文章の簡単な動画である。1+2+3+…=-1/12が視覚化されている。

上記の動画は自然数の無限和と二乗の無限和と三乗の無限和である。

#自己紹介 #とは #ゼータ関数 #リーマン予想 #数学 #無限級数 #1+2+3+4+…